|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
Основные цветовые модели, представление изображения, базовые операции над изображениями
Презентацию к лекции Вы можете скачать здесь.
Формирование изображений
Понятие цвета базируется на восприятии глазами человека электромагнитных волн в определенном диапазоне частот. Человеческий глаз воспринимает длины волн  от 400 нм (фиолетовый) до 700 нм (красный).
от 400 нм (фиолетовый) до 700 нм (красный).
Формирование цифрового изображения в камере происходит следующим образом. Свет, отражённый от объектов сцены, проходит через линзу (или систему линз) объектива камеры и фокусируется на сенсоре, который состоит из фотоэлементов, покрытых светофильтрами. Таким образом, отдельные ячейки сенсора формируют разные цветовые каналы. Чаще всего используются RGB (red, green, blue) светофильтры.
Следует отметить, что в процессе формирования изображения возникают различные искажения, такие как: радиальная дисторсия из-за геометрии линзы, блики из-за переотражений в оптической системе, смазанные участки изображения из-за ошибок фокусировки или выдержки, затемнённые или пересвеченные части изображения. Львиную часть этих искажений можно компенсировать с помощью методов цифровой обработки изображений, которая будет описана ниже.
Для упрощения математического описания процесса формирования изображения часто применяют так называемую модель pinhole камеры, в которой считается, что световые лучи проходят через малое отверстие и попадают на сенсор. При этом зависимость координат спроектированной точки и точки в мировой системе координат описывается уравнением перспективной проекции:
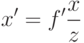

где 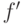 — фокусное расстояние,
— фокусное расстояние, 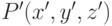 - координаты точки в системе координат камеры,
- координаты точки в системе координат камеры,  – координаты точки в мировой системе координат.
– координаты точки в мировой системе координат.
Данные с элементов сенсора считываются в двухмерный массив, который называют растром.
Следует отметить, что компьютерное зрение используется не только для обработки и анализа изображений, сформированных цветными или черно-белыми камерами, но и устройствами, позволяющими видеть сцену в инфракрасном, миллиметровом и других диапазонах электромагнитного спектра.
Типы изображений
Элементом растра является пиксель.
Каждый пиксель может содержать одно или несколько значений в зависимости от типа изображения.
Определение. Цифровое изображение – это двумерный массив ![I[r,c]](/sites/default/files/tex_cache/b5c8321d24b47f5b348f35a858f77b4f.png) элементов (пикселей), которые представляют собой одно или нескольких дискретных значений
элементов (пикселей), которые представляют собой одно или нескольких дискретных значений
Определение. Бинарное изображение – это цифровое изображение ![B[r,c]](/sites/default/files/tex_cache/cba04903048246439a0d04dab0d9e0fa.png) , пиксели которого принимают значения 0 или 1.
, пиксели которого принимают значения 0 или 1.
Определение. Полутоновое (синонимы: серое, монохромное, черно-белое) изображение – это цифровое изображение ![I[r,c]](/sites/default/files/tex_cache/b5c8321d24b47f5b348f35a858f77b4f.png) , у которого каждому пикселю соответствует одно значение интенсивности (яркости).
, у которого каждому пикселю соответствует одно значение интенсивности (яркости).
Определение. Мультиспектральное изображение – это цифровое изображение ![M[r,c]](/sites/default/files/tex_cache/e4a315c5c1d385e8eea3c5bc7cf8719b.png) , у которого каждому пикселю соответствует вектор значений.
, у которого каждому пикселю соответствует вектор значений.
У цветных изображений размерность этого вектора равна трём
В процессе решения задачи компьютерного зрения из исходного цветного изображения могут быть получены вспомогательные полутоновые или бинарные изображения. Для каждого класса изображений существуют свои методы обработки. Далее рассмотрим методы обработки бинарных изображений.
Обработка и анализ бинарных изображений
В системах компьютерного зрения бинарные изображения часто используются для выделения/маскирования определённых областей изображения для последующего анализа. Например, выделение областей букв для их дальнейшего распознавания. При этом ненулевыми значениями пикселов выделяются интересующие области.
Рассмотрим сначала методы получения бинарных изображений.
В некоторых случаях достаточно осуществить пороговую бинаризацию для выделения объектов. Пороговая бинаризация представляется фильтром

где A – исходное полутоновое изображение, B – выходное бинарное изображение.
В случае однотонных объектов порог бинаризации может быть выбран, анализируя гистограмму яркостей пикселов полутонового изображения. На изображении, представленном ниже, первый пик гистограммы соответствует наиболее популярному значению яркости фона, второй пик соответствует наиболее популярной яркости объекта. Порог следует выбирать между ними.
В некоторых случаях для нахождения порога может быть использован метод Отсу [ 1 ], который находит порог, минимизирующий вариацию яркостей пикселов в объекте и фоне.
В ходе получения бинарного изображения часто появляются шумовые пикселы, которые надо отфильтровать. Для фильтрации бинарных изображений часто используется морфологическая фильтрация.
Рассмотрим частные случаи морфологической фильтрации – сужение (erode), расширение (dilate), открытие (open), замыкание (close).
Фильтрация сужением осуществляется применением оператора минимума в окрестности


каждого пиксела бинарного изображения:
где element – структурный элемент морфологической операции, представляющий собой вспомогательное бинарное изображение, которое определяет окрестность, в которой действует оператор минимума.
Фильтрация расширением осуществляется применением оператора максимума в окрестности каждого пиксела бинарного изображения:


Фильтрация открытием состоит в последовательном применении фильтрации сужением, а затем расширением с одинаковым структурным элементом.
Фильтрация замыканием состоит в последовательном применении фильтрации расширением, а затем сужением с одинаковым структурным элементом.
Следует отметить, что операцию открытие применяют для фильтрации мелкого шума, а операцию замыкания для заполнения пробелов в объекте.
После морфологической фильтрации дальнейший анализ бинарного изображения может быть произведён посредством выделения связанных компонент на изображении.
Два пиксела называются связанными, если они расположены в соседних ячейках растра. При этом вводится понятие 4ёх и 8ми связанности. Пикселы 4ёх связанны, если они соседствуют по вертикали и горизонтали и 8ми связанны если ещё и по диагонали.
Так, например, на бинарном изображении представленном ниже присутствуют две 8ми связанные компоненты и четыре 4ёх связанные.
Существуют различные методы поиска и подсчёта связанных компонент (в [2] можно найти детали рекурсивного алгоритма).
Анализ выделенных связанных компонент может заключатся в вычислении значимых признаков, описывающих найденные объекты.
Перечислим некоторые из этих признаков: площадь S, периметр P, координаты описывающего прямоугольника, центр тяжести, округлость  (отношение квадрата периметра к площади), центральные и смешанные моменты.
(отношение квадрата периметра к площади), центральные и смешанные моменты.
Часто удобнее и значительно эффективнее анализировать связанные компоненты с помощью описывающего их контура. При этом не происходит потери информации, но значительно уменьшается её объём (пикселы, не принадлежащие границе объекта не несут информации).
Извлечение контуров объектов можно осуществить с помощью алгоритма [3], реализованного в библиотеке OpenCV.
Аппроксимация контура позволяет без существенной потери информации в разы уменьшить количество точек в контуре и значительно ускорить контурный анализ. Аппроксимация может быть осуществлена следующим алгоритмом:
- Находятся две самые удалённые друг от друга точки контура. Две части контура между ними рассматриваются независимо.
- Для каждого полученного участка контура находится точка наиболее удалённая от прямой соединяющей концевые точки участка.
- Если расстояние от точки, найденной на шаге 2 до прямой больше заданного порога, то эта часть контура разбивается этой точкой на два меньших участка.
- Если найденное расстояние меньше порога, то вместо этой части контура в результирующий контур сохраняется отрезок соединяющий концевые точки участка.
Шаги 2 и 3 повторяются для всех участков пока выполняется условие 3.
Процедуру можно проиллюстрировать следующим рисунком:
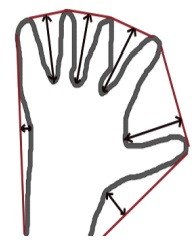
Контурное (векторное) представление позволяет, например, подсчитать количество дефектов выпуклости фигуры. Дефект выпуклости – это область не принадлежащая фигуре, но принадлежащая её выпуклой оболочке. Пример дефектов выпуклости контура кисти изображён ниже.