|
Я прошёл курс и сдал экзамены и тесты. Но изначально сертификат не заказывал. Могу ли я сейчас его заказать, оплатить и получить? Как это сделать? |
Методы и алгоритмы анализа структуры многомерных данных
Если процедура факторного анализа сжимает в малое число количественных переменных данные, описанные количественными переменными, то кластерный анализ сжимает данные в классификацию объектов. Синонимами термина "кластерный анализ" являются "автоматическая классификация объектов без учителя" и "таксономия".
Если данные понимать как точки в признаковом пространстве, то задача кластерного анализа формулируется как выделение "сгущений точек", разбиение совокупности на однородные подмножества объектов.
При проведении кластерного анализа обычно определяют расстояние на множестве объектов; алгоритмы кластерного анализа формулируют в терминах этих расстояний. Мер близости и расстояний между объектами существует великое множество. Их выбирают в зависимости от цели исследования. В частности, евклидово расстояние лучше использовать для количественных переменных, расстояние хи-квадрат — для исследования частотных таблиц, имеется множество мер для бинарных переменных.
Кластерный анализ является описательной процедурой, он не позволяет сделать никаких статистических выводов, но дает возможность провести своеобразную разведку — изучить "структуру совокупности".
Иерархический кластерный анализ
Процедура иерархического кластерного анализа в SPSS предусматривает группировку как объектов (строк матрицы данных), так и переменных (столбцов). Можно считать, что в последнем случае роль объектов играют переменные, а роль переменных — столбцы.
Этот метод реализует иерархический агломеративный алгоритм. Его смысл заключается в следующем. Перед началом кластеризации все объекты считаются отдельными кластерами, которые в ходе алгоритма объединяются. Вначале выбирается пара ближайших кластеров, которые объединяются в один кластер. В результате количество кластеров становится равным N-1. Процедура повторяется, пока все классы не объединятся. На любом этапе объединение можно прервать, получив нужное число кластеров. Таким образом, результат работы алгоритма агрегирования определяют способы вычисления расстояния между объектами и определения близости между кластерами.
Для определения расстояния между парой кластеров могут быть сформулированы различные разумные подходы. С учетом этого в SPSS предусмотрены следующие методы, определяемые на основе расстояний между объектами:
- Среднее расстояние между кластерами (Between-groups linkage).
- Среднее расстояние между всеми объектами пары кластеров с учетом расстояний внутри кластеров(Within-groups linkage).
- Расстояние между ближайшими соседями — ближайшими объектами кластеров (Nearest neighbor).
- Расстояние между самыми далекими соседями (Furthest neighbor).
- Расстояние между центрами кластеров (Centroid clustering).
- Расстояние между центрами кластеров (Centroid clustering), или центроидный метод. Недостатком этого метода является то, что центр объединенного кластера вычисляется как среднее центров объединяемых кластеров, без учета их объема.
- Метод медиан — тот же центроидный метод, но центр объединенного кластера вычисляется как среднее всех объектов (Median clustering).
- Метод Варда (Ward's method). В качестве расстояния между кластерами берется прирост суммы квадратов расстояний объектов до центров кластеров, получаемый в результате их объединения.
Расстояния и меры близости между объектами. У нас нет возможности сделать полный обзор всех коэффициентов, поэтому остановимся лишь на характерных расстояниях и мерах близости для определенных видов данных.
Меры близости отличаются от расстояний тем, что они тем больше, чем более похожи объекты.
Пусть имеются два объекта X=(X1,…,Xm) и Y=(Y1,…,Ym). Применяя эту запись для объектов, определить основные виды расстояний, используемых процедуре CLUSTER:
-
Евклидово расстояние
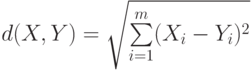 (Euclidian distance).
(Euclidian distance). - Квадрат евклидова расстояния
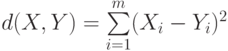 (Squared Euclidian distance)
(Squared Euclidian distance)
Эвклидово расстояние и его квадрат целесообразно использовать для анализа количественных данных.
- Мера близости — коэффициент корреляции
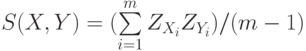 , где
, где 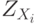 и
и 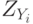 — компоненты стандартизованных векторов X и Y. Эту меру целесообразно использовать для выявления кластеров переменных, а не объектов.
— компоненты стандартизованных векторов X и Y. Эту меру целесообразно использовать для выявления кластеров переменных, а не объектов. - Расстояние хи-квадрат получается на основе таблицы сопряженности, составленной из объектов X и Y, которые, предположительно, являютсявекторами частот. Здесь рассматриваются ожидаемые значения элементов, равные E(Xi)=X.*(Xi+Yi)/(X.+Y.) и E(Yi)=Y.*(Xi+Yi)/(X.+Y.), а расстояние хи-квадрат имеет вид корня из соответствующего показателя
Таблица 5.1. Таблица для пары объектов — строк частот X X1 ... Xm X. Y Y1 ... Ym Y. X+Y X1+Y1 ... Xm+Ym X.+Y. 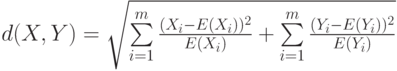 .
. - Расстояние Фи-квадрат является расстоянием хи-квадрат, нормированным "число объектов" в таблице сопряженности, представляемой строками X и Y, т.е. на корень квадратный из N=X.+Y..
- В иерархичесом кластерном анализе в SPSS также имеется несколько видов расстояний для бинарных данных (векторы X и Y состоят из нулей и единиц, обозначающих наличие или отсутствие определенных свойств объектов). Наиболее естественными из них, по видимому, являются евклидово расстояние и его квадрат.
Стандартизация
Непосредственное использование переменных в анализе может привести к тому, что классификацию будут определять переменные, имеющие наибольший разброс значений. Поэтому применяются следующие виды стандартизации:
- Z -шкалы (Z-Scores). Из значений переменных вычитается их среднее, и эти значения делятся на стандартное отклонение.
- Разброс от -1 до 1. Линейным преобразованием переменных добиваются разброса значений от -1 до 1.
- Разброс от 0 до 1. Линейным преобразованием переменных добиваются разброса значений от 0 до 1.
- Максимум 1. Значения переменных делятся на их максимум.
- Среднее 1. Значения переменных делятся на их среднее.
- Стандартное отклонение 1. Значения переменных делятся на стандартное отклонение.
- Кроме того, возможны преобразования самих расстояний, в частности, можно расстояния заменить их абсолютными значениями, это актуально для коэффициентов корреляции. Можно также все расстояния преобразовать так, чтобы они изменялись от 0 до 1.
Таким образом, работа с кластерным анализом может превратиться в увлекательную игру, связанную с подбором метода агрегирования, расстояния и стандартизации переменных с целью получения наиболее интерпретируемого результата. Желательно только, чтобы это не стало самоцелью и исследователь получил действительно необходимые содержательные сведения о структуре данных.
Процесс агрегирования данных может быть представлен графически деревом объединения кластеров (Dendrogramm) либо "сосульковой" диаграммой (Icicle).
Но подробнее о процессе кластеризации можно узнать по протоколу объединения кластеров (Schedule).Пример иерархического кластерного анализа. Проведем кластерный анализ по полученным нами ранее факторам на агрегированном файле Курильского опроса:
CLUSTER fac1_1 fac2_1 /METHOD BAVERAGE /MEASURE= SEUCLID /ID=name /PRINT SCHEDULE CLUSTER(3,5) /PLOT DENDROGRAM .
В команде указаны переменные fac1_1 fac2_1 для кластеризации. По умолчанию расстояние между кластерами определяется по среднему расстоянию между объектами ( METHOD BAVERAGE ), а расстояние между объектами — как квадрат евклидова ( MEASURE= SEUCLID ). Кроме того, распечатывается протокол ( PRINT SCHEDULE ), в качестве переменных выводятся классификации из 3, 4, 5 кластеров ( CLUSTER(3,5) ) и строится дендрограмма ( PLOT DENDROGRAM ).
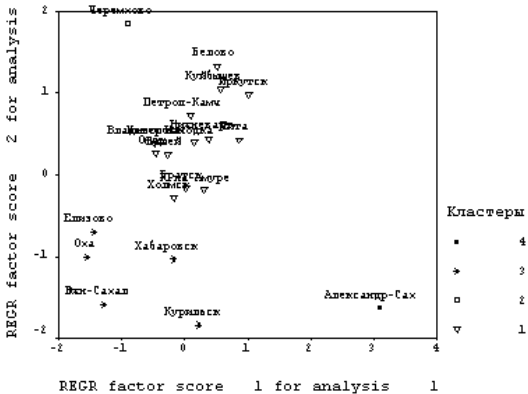
Разрез дерева агрегирования (рис. 5.2) вертикальной чертой на четыре части дал два кластера, состоящих из уникальных по своим характеристикам городов Александровск-Сахалинский и Черемхово; кластер из 5 городов (Оха, Елизово, Южно-Сахалинск, Хабаровск, Курильск); еще один кластер из 14 городов составили последний кластер.
Естественность такой классификации демонстрирует полученное поле рассеяния данных (рис.5.3).
Процесс объединения подробно показан в протоколе объединения (табл. 5.2). В нем указаны стадии объединения, объединяемые кластеры (после объединения кластер принимает минимальный номер из номеров объединяемых кластеров). Далее следует расстояние между кластерами, номер стадии, на которой кластеры ранее уже участвовали в объединении; затем следующая стадия, где произойдет объединение с другим кластером.
На практике интерпретация кластеров требует достаточно серьезной работы, изучения разнообразных характеристик объектов для точного описания типов объектов, которые составляют тот или иной класс.