|
Добрый день! В курсе "Проектирование систем искусственного интеллекта" начал проходить обучение и сдал тесты по лекциям 1,2,3,4. Но видимо из-за того что не записался на курс, после того как записался на курс у меня затерлись результаты сданных тестов. Можно как-то исправить (восстановить результаты по тестам 1,2,3,4) ? |
Адаптация и обучение
Метод предельных упрощений (МПУ)
По тому, как организован процесс обучения распознающих систем, четко выделяются два подхода к проблеме ОРО. Первый основан на построении сложных разделяющих поверхностей в случайно выбранных пространствах, а во втором центр тяжести проблемы переносится на достижение понимания принципов формирования такого описания объектов, в рамках которого сам процесс распознавания чрезвычайно прост. Обучение в этом случае рассматривается как некий процесс конструирования пространств для решения конкретных задач.
В МПУ предполагается, что разделяющая функция задается заранее в виде линейного (самого простого) полинома, а процесс обучения состоит в конструировании такого пространства минимальной размерности, в котором заранее заданная наиболее простая разделяющая функция безошибочно разделяет обучающую последовательность. МПР назван так потому, что в нем строится самое простое решающее правило в пространстве небольшой размерности, т. е. в простом пространстве.
Пусть на некотором множестве объектов V заданы два подмножества 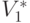 и
и 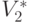 , определяющие собой образы на обучающей последовательности V. Рассмотрим i -е свойство объектов, такое, что некоторые объекты обучающей последовательности этим свойством обладают, а другие — нет. Пусть заданным свойством обладают объекты, образующие подмножество V1i, а объекты подмножества V2i этим свойством не обладают (
, определяющие собой образы на обучающей последовательности V. Рассмотрим i -е свойство объектов, такое, что некоторые объекты обучающей последовательности этим свойством обладают, а другие — нет. Пусть заданным свойством обладают объекты, образующие подмножество V1i, а объекты подмножества V2i этим свойством не обладают (  ). Тогда i -е свойство называют признаком первого типа относительно образа
). Тогда i -е свойство называют признаком первого типа относительно образа 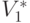 , если выполняются соотношения
, если выполняются соотношения
 |
( 4.50) |
и признаком второго типа, если выполняются
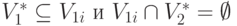 |
( 4.51) |
Если же выполняются соотношения
 |
( 4.52) |
то i -е свойство считается признаком первого типа относительно образа 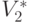 , а если выполняются
, а если выполняются
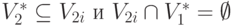 |
( 4.53) |
то это же свойство объявляется признаком второго типа относительно образа 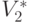 . Если свойство не обладает ни одной из приведенных особенностей, то оно вообще не относится к признакам и не участвует в формировании пространства.
. Если свойство не обладает ни одной из приведенных особенностей, то оно вообще не относится к признакам и не участвует в формировании пространства.
Одинаковые признаки — это два признака xi и xj, порождающие подмножества V1j, V2j, V1i, V2i, такие, что
V1j= V1i и V2j= V2i.(4.54)
Доказано утверждение, смысл которого заключается в том, что если пространство конструировать из однотипных, но неодинаковых признаков, то в конце концов будет построено такое пространство, в котором обучающая последовательность будет безошибочно разделена на два образа линейным, т. е. самым простым, решающим правилом.
Метод предельных упрощений состоит в том, что в процессе обучения последовательно проверяются все возможные свойства объектов и из них выбираются только такие, которые обладают хотя бы одной из особенностей, определяемых соотношениями (4.50), (4.51). Такой отбор однотипных, но неодинаковых признаков продолжается до тех пор, пока при некотором значении размерности пространства не наступит безошибочное линейное разделение образов на обучающей последовательности. В зависимости от того, из признаков какого типа строится пространство, в качестве разделяющей плоскости выбирается плоскость, описываемая уравнением
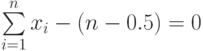 |
( 4.55) |
либо уравнением
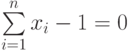 |
( 4.56) |
Каждый объект относится к одному из образов в зависимости от того, по какую сторону относительно плоскости находится соответствующий этому объекту вектор в пространстве признаков размерности n.
Коллективы решающих правил
Давно известны приемы повышения качества принимаемых решений, состоящие в объединении специалистов той или иной области знаний в коллектив, вырабатывающий совместное решение. Идею коллективного решения можно применить и к "коллективу" формальных алгоритмов, что позволит повысить эффективность решения многих задач.
Для рационального использования особенностей различных алгоритмов при решении задач распознавания возможно объединить различные по характеру алгоритмы распознавания в коллективы, которые формируют классификационное решение на основе правил, принятых в теории коллективных решений. Пусть в некоторой ситуации Х принимается решение S. Тогда S=R(X), где R — алгоритм принятия решения в ситуации X. Предположим, что существует L различных алгоритмов решения задачи, т. е. Sl=Rl(X), l=1, 2, ... , L, где Sl — решение, полученное алгоритмом Rl. Будем называть множество алгоритмов {R}={R1, R2, ..., Ri.} коллективом алгоритмов решения задачи (коллективом решающих правил), если на множестве решений Sl в любой ситуации Х определено решающее правило F, т. е. S=F(S1, S2, ..., SL, X). Алгоритмы Rl принято называть членами коллектива, Sl — решением l -го члена коллектива, а S — коллективным решением. Функция F определяет способ обобщения индивидуальных решений в решения коллектива S. Поэтому синтез функции F, или способ обобщения, является центральным моментом в организации коллектива.
Принятие коллективного решения может быть использовано при решении различных задач. Так, в задаче управления под ситуацией понимается ситуация среды и целей управления, а под решением — самоуправление, приводящее объект в целевое состояние. В задачах прогноза Х — исходное, а S — прогнозируемое состояние. В задачах распознавания ситуацией Х является описание объекта X, т. е. его изображение, а решением S — номер образа, к которому принадлежит наблюдаемое изображение. Индивидуальное и коллективное решения в задаче распознавания состоят в отнесении некоторого изображения к одному из образов. Наиболее интересными коллективами распознающих алгоритмов являются такие, в которых существует зависимость веса каждого решающего правила Rl от распознаваемого изображения. Например, вес решающего правила Rl может определяться соотношением
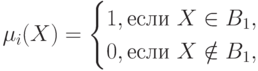 |
( 4.57) |
где Bl — область компетентности решающего правила Rl. Веса решающих правил выбираются так, что
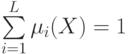 |
( 4.58) |
для всех возможных значений X. Соотношение (4.57) означает, что решение коллектива определяется решением того решающего правила Ri, области компетентности которого принадлежит изображение объекта X. Такой подход представляет собой двухуровневую процедуру распознавания. На первом уровне определяется принадлежность изображения той или иной области компетентности, а уже на втором — вступает в силу решающее правило, компетентность которого максимальна в найденной области. Решение этого правила отождествляется с решением всего коллектива. Основным этапом в такой организации коллективного решения является обучение распознаванию областей компетентности. Практически постановкой этой задачи различаются правила организации решения коллектива. Области компетентности можно искать, используя вероятностные свойства правил коллектива, можно применить гипотезу компактности и считать, что одинаковым правилам должны соответствовать компактные области, которые можно выделить алгоритмами самообучения. В процессе обучения сначала выделяются компактные множества и соответствующие им области, а затем в каждой из этих областей восстанавливается свое решающее правило. Решение такого правила, действующего в определенной области, объявляется диктаторским, т. е. отождествляется с решением всего коллектива.
В персептроне каждый A -элемент может интерпретироваться как член коллектива. В процессе обучения все A -элементы приобретают веса, в соответствии с которыми эти A -элементы участвуют в коллективном решении. Особенность каждого A -элемента состоит в том, что он действует в некотором подпространстве исходного пространства, характер которого определяется связями между S - и A -элементами. Решение, получаемое на выходе персептрона, можно интерпретировать как средневзвешенное решение коллектива, состоящего из всех A -элементов.
