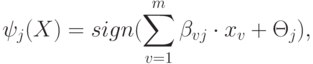|
Я прошёл курс и сдал экзамены и тесты. Но изначально сертификат не заказывал. Могу ли я сейчас его заказать, оплатить и получить? Как это сделать? |
Адаптация и обучение
Метод потенциальных функций
Предположим, что требуется разделить два непересекающихся образа V1 и V2. Это значит, что в пространстве изображений существует, по крайней мере, одна функция, которая полностью разделяет множества, соответствующие образам V1 и V2. Эта функция должна принимать положительные значения в точках, которые соответствуют объектам, принадлежащим образу V1, и отрицательные — в точках образа V2. В общем случае таких разделяющих функций может быть много, тем больше, чем компактней разделяемые множества. В процессе обучения требуется построить одну из этих функций, иногда в некотором смысле наилучшую.
Метод потенциальных функций связан со следующей процедурой. В процессе обучения с каждой точкой пространства изображений, соответствующей единичному объекту из обучающей последовательности, связывается функция U(X, Xi), заданная на всем пространстве и зависящая от Xi как от параметра. Такие функции называются потенциальными, так как они напоминают функции потенциала электрического поля вокруг точечного электрического заряда. Изменение потенциала электрического поля по мере удаления от заряда обратно пропорционально квадрату расстояния. Потенциал, таким образом, может служить мерой удаления точки от заряда. Когда поле образовано несколькими зарядами, потенциал в каждой точке этого поля равен сумме потенциалов, создаваемых в этой точке каждым из зарядов. Если заряды, образующие поле, расположены компактной группой, потенциал поля будет иметь наибольшее значение внутри группы зарядов и убывать по мере удаления от нее.
Обучающей последовательности объектов соответствует последовательность векторов X1, X2, …, с которыми в пространстве изображений связана последовательность U(X, X1), U(X, X2), … потенциальных функций, используемых для построения функций f(X1, X2, …). По мере увеличения числа объектов в процессе обучения функция f должна стремиться к одной из разделяющих функций. В результате обучения могут быть построены потенциальные функции для каждого образа:
 |
( 4.35) |
В качестве разделяющей функции f(X) можно выбрать функцию вида:
f(X)=U1(X)-U2(X),(4.36)
которая положительна для объектов одного образа и отрицательна для объектов другого.
В качестве потенциальной функции рассмотрим функцию вида
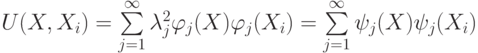 |
( 4.37) |
где 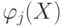 — линейно независимая система функций;
— линейно независимая система функций; 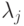 — действительные числа, отличные от нуля для всех j = 1, 2, … ; Xi — точка, соответствующая i -му объекту из обучающей последовательности. Предполагается, что
— действительные числа, отличные от нуля для всех j = 1, 2, … ; Xi — точка, соответствующая i -му объекту из обучающей последовательности. Предполагается, что 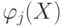 и U(X, Xi) ограничены при
и U(X, Xi) ограничены при 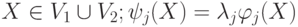 .
.
В процессе обучения предъявляется обучающая последовательность и на каждом n-м такте обучения строится приближение fn(X), которое характеризуется следующей основной рекуррентной процедурой:
fn+1(X)=qnfn(X)+rnU(Xn+1,X),(4.38)
Разновидности алгоритмов потенциальных функций отличаются выбором значений qn и rn, которые являются фиксированными функциями номера n. Как правило, 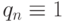 , а rn выбирается в виде:
, а rn выбирается в виде:
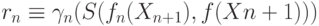 |
( 4.39) |
где S(fn, f) — невозрастающие функции, причем
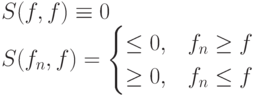 |
( 4.40) |
Коэффициенты  представляют собой неотрицательную числовую последовательность, зависящую только от номера n. Кроме того,
представляют собой неотрицательную числовую последовательность, зависящую только от номера n. Кроме того, 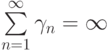 и
и 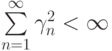 (например,
(например, 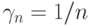 ) или
) или 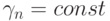 .
.
Разработано несколько вариантов алгоритмов потенциальных функций, различие между которыми состоит в выборе законов коррекции разделяющей функции от шага к шагу, т. е. в выборе законов коррекции разделяющей функции от шага к шагу, иными словами, в выборе коэффициентов rn. Приведем два основных алгоритма потенциальных функций.
-
Будем считать, что
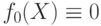 (нулевое приближение). Пусть в результате применения алгоритма после n -го шага построена разделяющая функция fn(X), а на (n+1) -м шаге предъявлено изображение Xn+1, для которого известно действительное значение разделяющей функции f(Xn+1 ). Тогда функция fn+1(X) строится по следующему правилу:
(нулевое приближение). Пусть в результате применения алгоритма после n -го шага построена разделяющая функция fn(X), а на (n+1) -м шаге предъявлено изображение Xn+1, для которого известно действительное значение разделяющей функции f(Xn+1 ). Тогда функция fn+1(X) строится по следующему правилу: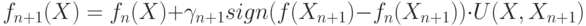
( 4.41) -
Во втором алгоритме также принимается, что
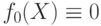 . Переход к следующему приближению, т. е. переход от функции fn(X) к fn+1(X), осуществляется в результате следующей рекуррентной процедуры:
. Переход к следующему приближению, т. е. переход от функции fn(X) к fn+1(X), осуществляется в результате следующей рекуррентной процедуры: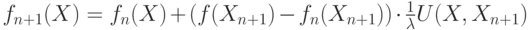
( 4.42) где
 — произвольная положительная константа, удовлетворяющая условию
— произвольная положительная константа, удовлетворяющая условию  .
.
Если в (ф. 5) принять