Основы машинной графики

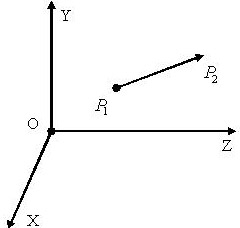
Изменим теперь положение координатных осей левосторонней системы координат таким образом, чтобы ось OY была направлена в плоскость рисунка. Тогда положительная полуось OZ будет направлена горизонтально вправо, а положительная полуось OX - вертикально вверх (рис. 1.10).

Получить формулу вращения точки вокруг оси OY на угол можно заменив x на z, y на x в формуле двумерного поворота. При этом координата точки y при таком вращении не изменяется. В результате чего формула вращения точки (x,y,z) вокруг оси OY на угол будет иметь следующий вид:

или в матричной форме

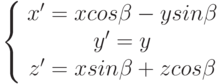
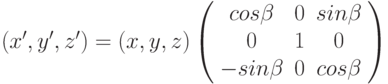
Аналогично поступаем с осью вращения OX. Изменим положение координатных осей так, чтобы ось OX была направлена в плоскость рисунка, ось OY - горизонтально вправо, ось OZ - вертикально вверх (рис. 1.11).

Заменив в формуле двумерного поворота y на z, x на y, получим формулу вращения точки (x,y,z) вокруг оси OX на угол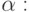

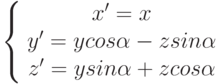
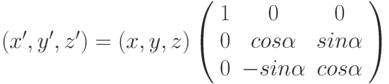
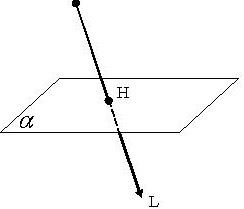
или в матричной форме

Способ двумерного плоского вращения вокруг произвольной точки может быть обобщен на случай вращения вокруг произвольной оси трехмерного пространства. Пусть произвольная ось вращения задается вектором , причем 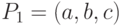- точка, определяющая начало вектора, а 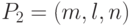- конец вектора (рис. 1.12)

Вращение вокруг задаваемой оси (вектора ) на угол выполняется в несколько этапов:

1. Перенос вектора так, чтобы начало вектора (точка 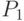) совпала с началом системы координат. Это осуществляется с помощью операции сдвига T(-a,-b,-c) ;
2. Поворот вокруг оси OY на угол так, чтобы вектор (m,l,n) оказался в плоскости OYZ: ;
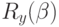3. Поворот вокруг оси OX на угол так, чтобы вектор (m',l',n') совпал с осью OZ: ;
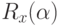4. Поворот вокруг оси OZ на заданный угол ;
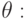
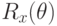5. Выполнение преобразования, обратного, произведенному на шаге 3. Т.е. поворот вокруг оси OX на угол ;
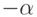6. Выполнение преобразования, обратного, произведенному на шаге 2. Т.е. поворот вокруг оси OY на угол ;
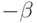7. Выполнение преобразования, обратного, произведенному на шаге 1. Т.е. сдвиг на вектор (a,b,c): T(a,b,c)

Данный алгоритм вращения вокруг произвольной оси можно записать с помощью произведения серии элементарных матриц: 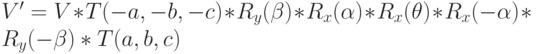, где V - исходная точка, V' - точка после поворота.

Остается определить чему равны углы поворотов и (рис. 1.13).

Из простых тригонометрических соотношений можно получить следующие формулы:

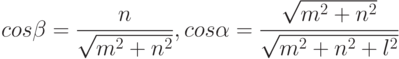
Как видно, операции трехмерного масштабирования и вращения могут быть реализованы с помощью умножения вектор-строки (точки) на матрицу преобразования. Операция же сдвига реализуется через сложение двух вектор-строк. Аналогично тому, как все двумерные преобразования (сдвиг, масштабирование и вращение) описываются матрицами размером 3х3 (через однородные координаты), трехмерные преобразования могут быть представлены в виде матриц размером 4х4. И тогда точка трехмерного пространства (x,y,z) записывается в однородных координатах как Wx,Wy,Wz,W, где . Если 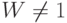, то для получения трехмерных декартовых координат точки (x,y,z) первые три однородные координаты нужно разделить на W. Отсюда следует, что две точк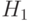и и 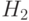в пространстве однородных координат описывают одну и ту же точку трехмерного пространства в том и только том случае, когда для любой константы c не равной нулю. Таким образом, преобразование точки трехмерного пространства P=(x,y,z) в новую точку P'=(x',y',z') с использованием однородных координат можно записать как:

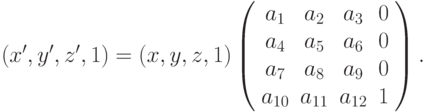
Уравнения трехмерного сдвига, масштабирования и вращения записываются в виде матриц преобразования однородных координат следующим образом:

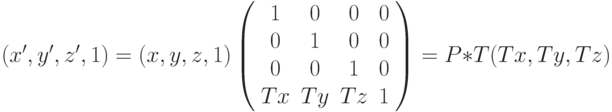
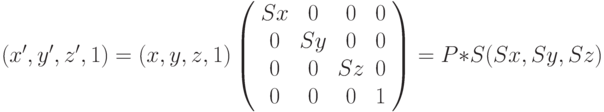
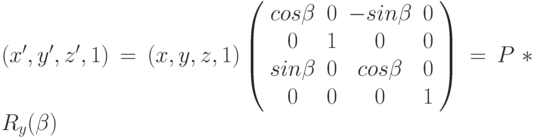
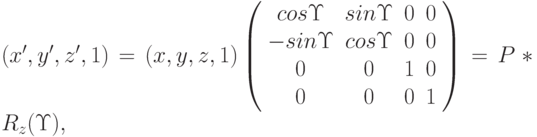
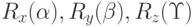где Tx,Ty,Tz - величины сдвига по осям OX, OY, OZ соответственно, Sx,Sy,Sz - масштабные множители по OX,OY,OZ соответственно, - матрицы вращения вокруг осей OX,OY,OZ на углы 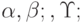соответственно.

Как и в двумерном случае, матричный подход позволяет совместить два или более элементарных преобразования в одно. Таким образом, последовательное применение двух преобразовани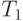й и 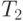может быть заменено применением одного преобразования T, причем матрица T будет равна произведению матриц преобразовани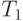й и 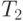. Это легко можно увидеть на простом примере. Пусть точка (x,y,z) трансформируется в точку (x',y',z') с помощью преобразования 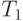: 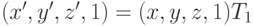. Применяя затем преобразование 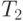к точке (x',y',z'), получим точку 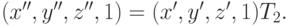Теперь подставляя первое выражение во второе, получим: 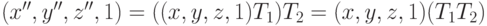. Причем порядок применения преобразований должен быть сохранен при перемножении соответствующих матриц.

Процесс вывода трехмерной графической информации по существу является более сложным, чем соответствующий двумерный процесс. Сложность, характерная для трехмерного случая, обуславливается тем, что поверхность вывода не имеет графического третьего измерения. Такое несоответствие между пространственными объектами и плоскими изображениями устраняется путем введения проекций, которые отображают трехмерные объекты на двумерной проекционной картинной плоскости. В процессе вывода трехмерной графической информации мы задаем видимый объем в мировом пространстве, проекцию на картинную плоскость и поле вывода на видовой поверхности. В общем случае объекты, определенные в трехмерном мировом пространстве, отсекаются по границам трехмерного видимого объема и после этого проецируются. То, что попадает в пределы окна, которое само является проекцией видимого объема на картинную плоскость, затем преобразуется в поле вывода и отображается на графическом устройстве. В общем случае операция проекции преобразует точки, заданные в системе координат размерности n, в точки системы координат размерности меньшей, чем n. В нашем случае точка трехмерного пространства отображается в двумерное пространство. Проекция трехмерного объекта строится при помощи прямых проецирующих лучей, которые называются проекторами и которые выходят из центра проекции, проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию. На рис. 1.14 представлены две различные проекции одного и того же отрезка и проекторы, проходящие через его конечные точки.

Определенный таким образом класс проекций известен под названием плоских геометрических проекций, т.к. проецирование осуществляется на плоскость, а не на искривленную поверхность и в качестве проекторов используют прямые линии. Плоские геометрические проекции можно подразделить на два основных класса: центральные (перспективные) и параллельные (ортогональные). Различие между ними определяется соотношением между центром проекции и проекционной плоскостью. Так, если расстояние между ними, конечно, то проекция будет центральной, если же оно бесконечно, то – параллельной. При описании центральной проекции мы явно задаем ее центр проекции, в то время как для параллельной проекции мы указываем лишь направление проецирования. Центр проекции порождает визуальный эффект, аналогичный тому, к которому приводят фотографические системы и используется в случаях, когда желательно достичь некоторой степени реализма. Следует заметить, что размер центральной проекции объекта изменяется обратно пропорционально расстоянию от центра проекции до объекта. Параллельная проекция порождает менее реалистичное изображение, т.к. отсутствует перспективное "укорачивание" объекта. Проекция фиксирует истинные размеры объекта, и параллельные линии остаются параллельными.

В общем случае задача получения центральной проекции заключается в том, чтобы определить проекцию точки объекта, расположенную в произвольном месте трехмерного пространства, на некоторую плоскость в этом же пространстве, называемую картинной. Нахождение центральной проекции является частным случаем задачи определения пересечения луча L с плоскостью в трехмерном пространстве (рис. 1.15)

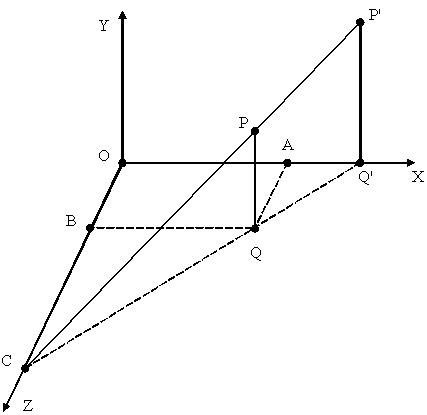
В машинной графике задача вычисления центральной проекции, как правило, сильно упрощена. В данном случае центр проекции, который также называют точкой зрения, находится на одной из осей системы координат, картинная (проекционная) плоскость перпендикулярна оптической оси. Как правило, точку зрения (центр проекции) располагают на оси OZ, тогда картинная плоскость будет параллельна плоскости OXY системы координат (рис. 1.16).

В нашем случае точка C=(0,0,c) - центр проекции (положение наблюдателя), плоскость z=0 - картинная плоскость. Пусть точка P=(x,y,z) имеет проекцию P'=(x',y',0). Рассмотрим два подобных треугольника CPQ и CP'Q', и запишем отношение катетов: . Рассмотрим два других подобных треугольника CQ'O и CQB, и запишем отношения сторон для них: . С другой стороны имеем: 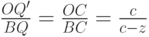. Так как OQ'=x', BQ=x, P'Q'=y', PQ=y имеем

или после преобразований

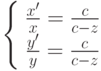
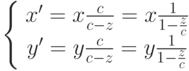
Если теперь c стремится к бесконечности, то получим формулу параллельной проекции: .

Следующим шагом необходимо спроецированное изображение перевести в координаты экрана. Это можно проделать следующим образом:

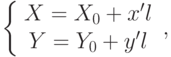
где - середина экрана, l - количество пикселей в единице.

Существует связь однородных координат с операцией центральной и параллельной проекциями, которая может быть выражена так: .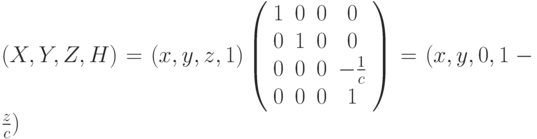

Для перехода от однородных координат к обычным, необходимо разделить все компоненты точки на четвертую координату: .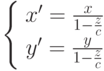

Для параллельной проекции матрица преобразования будет иметь вид: .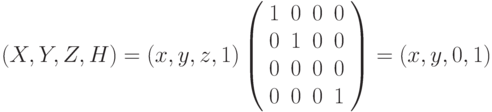

Таким образом, шаг проецирования можно описать в терминах матричной операции умножения. В результате этого мы можем объединить вместе операции преобразования объекта (сдвиг, масштабирование, вращение) и операцию проецирования в одну общую матрицу преобразования. Аналогично можно поступить с приведением спроецированных точек к экранным координатам:

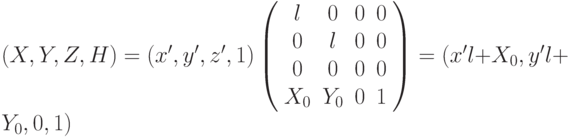
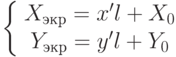
Таким образом, все операции преобразования объекта трехмерного пространства на картинную плоскость (экран) можно описать в терминах матричных умножений.