Настройка и ускорение программ в OpenMP

Зависимости по данным

При распараллеливании программ, написанных с использованием OpenMP, надо стремиться к максимально большей независимости параллельных потоков друг от друга. При этом следует избегать ситуаций, когда одни параллельные потоки используют данные из других. Если таких ситуаций нет, то говорят, что параллельные потоки независимы по данным.

Таким образом, при разработке параллельных программ с применением OpenMP важно, анализируя параллельные алгоритмы, находить в них зависимости по данным и стараться устранять их по мере возможности. Часто зависимости по данным между петлями циклов могут быть исключены с помощью модификации алгоритмов. Ниже представлен пример цикла с зависимостью по данным между петлями цикла.

DO I = 2 , 5 
   A (I) = C * A (I -1) 
ENDDO

Далее представлено элементарное распараллеливание этого цикла:

c$omp parallel sections 
c$omp section 
  A (2) = C * A (1) 
c$omp section 
  A (3) = C * C * A (1) 
c$omp section 
  A (4) = C * C * C *A (1) 
c$omp section 
  A (5) = C * C * C * C * A (1) 
c$omp end sections nowait

Рассмотрим еще один пример программы с циклом, петли которого содержат зависимости по данным. Исходный фрагмент этой программы приведен в примере 6.4.

В примере 6.5 представлен пример распараллеленной версии программы. При распараллеливании вычисления индексов массивов были устранены операторы вычисления индексов по рекуррентным формулам.

Еще один характерный пример фрагмента программы с зависимостью по данным приведен в примере 6.6.

Распараллеливание этого фрагмента можно осуществить путем применения директивы OpenMP reduction к циклу do.

i1 = 0
   i2 = 0
do i =1, n
      i1 = i1 + 1
      B(i1) = …

      i2 = i2 + i
      A(i2) = …
enddo

c$omp parallel do
   do i =1, n
      B( i ) = …
      
      A((i**2 +i)/2) = …
   enddo

do i = 1, n
   xsum = xsum + a (i)
   xmu1 = xmu1 * a (i)
   xmax = max (xmax, a (i))
   xmin = min (xmin, a (i))
enddo

Из сказанного выше следует, что для эффективного распараллеливания циклов нужно по возможности обеспечить независимость петель вложенных циклов. При этом надо иметь в виду, что циклы с условными выходами, пример которых показан во фрагменте программы (пример 6.7), не распараллеливаются.

При распараллеливании вложенных циклов надо стремиться к вынесению независимых по данным петель циклов на верхний уровень и проводить распараллеливание только на этом уровне. Пример такого цикла приведен во фрагменте программы (пример 6.8). Распараллеливание такого цикла возможно только на самом верхнем уровне, т. е. по индексу k.

do i = 1, n
        a (i) = b (i) + c (i)
        if (a(i) .GT. amax) then
            a(i) = amax
            goto 100
        endif
    enddo
100 continue

do k = 1, n
   do j = 1, n
      do i = 1, n
         a (i, j) = a (i, j) + b (i, k) * c (k, j)
      enddo
   enddo
enddo

Эффективность параллельных программ и масштабируемость

После создания работающей параллельной программы обычно возникает проблема оценки ее эффективности. Под эффективностью параллельной программы понимают оценку ускорения, которое удается получить при переходе от последовательной версии программы к параллельной. Понятно, что такая оценка будет зависеть от числа параллельных процессоров.

Под масштабируемостью параллельной программы понимают изменение этой оценки в зависимости от числа параллельных процессоров.

Впервые теоретическая оценка эффективности параллельных программ предложена в работе [6.9]. В настоящее время эта оценка известна как закон Амдала, согласно которому максимальное ускорение A на параллельной вычислительной системе, содержащей p процессоров, удовлетворяет следующему неравенству

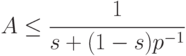
Здесь s - суммарная доля последовательных блоков в параллельной программе. Понятно, что 0<s<1.

Из закона Амдала следует, что при числе параллельных процессоров, стремящемся к бесконечности, максимальное ускорение A не превысит величины 1/s вне зависимости от качества реализации параллельной части программы. При этом, если половина программы представляет из себя последовательную часть s=1/2, то ускорить такую программу более чем в два раза не удастся при любом числе параллельных процессоров.

Еще одна интересная оценка, следующая из закона Амдала: для того чтобы ускорить программу на 8 параллельных процессорах, например в четыре раза, необходимо обеспечить, чтобы последовательная часть программы не превышала 1/7 части программы.

Таким образом, из закона Амдала видно, что при наличии в параллельных программах даже весьма незначительных последовательных частей происходит весьма существенное снижение быстродействия таких программ.