Методы контекстного моделирования
Терминология
Под контекстным моделированием будем понимать оценку вероятности появления символа (элемента, пиксела, сэмпла, отсчета и даже набора качественно разных объектов) в зависимости от непосредственно ему предшествующих, или контекста.
Заметим, что в быту понятие "контекст" обычно используется в глобальном значении - как совокупность символов (элементов), окружающих текущий обрабатываемый. Это контекст в широком смысле. Выделяют также "левосторонние" и "правосторонние" контексты, т.е. последовательности символов, непосредственно примыкающие к текущему символу слева и справа соответственно. Здесь и далее под контекстом будем понимать именно классический левосторонний: так, например, для последнего символа 'о' последовательности "…молоко…" контекстом является "…молок".
Если длина контекста ограничена, то такой подход будем называть контекстным моделированием ограниченного порядка (finite-context modeling), при этом под порядком понимается максимальная длина используемых контекстов N. Например, при моделировании порядка 3 для последнего символа 'о' в последовательности "…молоко…" контекстом максимальной длины 3 является строка "лок". При сжатии этого символа под "текущими контекстами" могут пониматься "лок", "ок", "к", а также пустая строка "". Все эти контексты длины от N до 0 назовем активными контекстами в том смысле, что при оценке символа может быть использована накопленная для них статистика.
Далее вместо "контекст длины o, 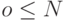 /" мы будем обычно говорить "контекст порядка o".
/" мы будем обычно говорить "контекст порядка o".
В силу объективных причин - ограниченность вычислительных ресурсов - техника контекстного моделирования именно ограниченного порядка получила наибольшее развитие и распространение, поэтому далее под контекстным моделированием будем понимать именно ее. Дальнейшее изложение также учитывает специфику того, что контекстное моделирование практически всегда применяется как адаптивное.
Оценки вероятностей при контекстном моделировании строятся на основании обычных счетчиков частот, связанных с текущим контекстом. Если мы обработали строку "абсабвбабс", то для контекста "аб" счетчик символа 'c' равен двум (говорят, что символ 'c' появился в контексте "аб" два раза), символа 'в' - единице. На основании этой статистики можно утверждать, что вероятность появления 'c' после "аб" равна 2/3, а вероятность появления 'в' - 1/3, т.е. оценки формируются на основе уже просмотренной части потока.
В общем случае для каждого контекста конечной длины 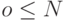 , встречаемого в обрабатываемой последовательности, создается контекстная модель КМ. Любая КМ включает в себя счетчики всех символов, встреченных в соответствующем ей контексте, т.е. сразу после строки контекста. После каждого появления какого-то символа s в рассматриваемом контексте производится увеличение значения счетчика символа s в соответствующей контексту КМ. Обычно счетчики инициализируются нулями. На практике счетчики обычно создаются по мере появления в заданном контексте новых символов, т.е. счетчиков ни разу не виденных в заданном контексте символов просто не существует.
, встречаемого в обрабатываемой последовательности, создается контекстная модель КМ. Любая КМ включает в себя счетчики всех символов, встреченных в соответствующем ей контексте, т.е. сразу после строки контекста. После каждого появления какого-то символа s в рассматриваемом контексте производится увеличение значения счетчика символа s в соответствующей контексту КМ. Обычно счетчики инициализируются нулями. На практике счетчики обычно создаются по мере появления в заданном контексте новых символов, т.е. счетчиков ни разу не виденных в заданном контексте символов просто не существует.
Под порядком КМ будем понимать длину соответствующего ей контекста. Если порядок КМ равен o, то будем обозначать такую КМ как "КМ(o)".
Кроме обычных КМ, часто используют контекстную модель минус первого порядка КМ(-1), присваивающую одинаковую вероятность всем символам алфавита сжимаемого потока.
Понятно, что для нулевого и минус первого порядка контекстная модель одна, а КМ большего порядка может быть несколько, вплоть до  где q - размер алфавита обрабатываемой последовательности. КМ(0) и КМ(-1) всегда активны.
где q - размер алфавита обрабатываемой последовательности. КМ(0) и КМ(-1) всегда активны.
Заметим, что часто не делается различий между понятием "контекст" и "контекстная модель". Авторы этой книги такое соглашение не поддерживают.
Часто говорят о "родительских" и "дочерних" контекстах. Для контекста "к" дочерними являются "ок" и "лк", поскольку они образованы сцеплением (конкатенацией) одного символа и контекста "к". Аналогично, для контекста "лок" родительским является контекст "ок", а контекстами-предками - "ок", "к", "". Очевидно, что "пустой" контекст "" является предком для всех. Аналогичные термины применяются для КМ, соответствующих контекстам.
Совокупность КМ образует модель источника данных. Под порядком модели понимается максимальный порядок используемых КМ.
Виды контекстного моделирования
Пример обработки строки "абсабвбабс" иллюстрирует сразу две проблемы контекстного моделирования:
- как выбирать подходящий контекст (или контексты) среди активных с целью получения более точной оценки, ведь текущий символ может лучше предсказываться не контекстом второго порядка "аб", а контекстом первого порядка "б";
- как оценивать вероятность символов, имеющих нулевую частоту (например, 'г').
Выше были приведены цифры, в соответствии с которыми при увеличении длины используемого контекста сжатие данных улучшается. К сожалению, при кодировании блоков типичной длины - единицы мегабайтов и меньше - это справедливо только для небольших порядков модели, т.к. статистика для длинных контекстов медленно накапливается. При этом также следует учитывать, что большинство реальных данных характеризуется неоднородностью, нестабильностью силы и вида статистических взаимосвязей, поэтому "старая" статистика контекстно-зависимых частот появления символов малополезна или даже вредна. Поэтому модели, строящие оценку только на основании информации КМ максимального порядка N, обеспечивают сравнительно низкую точность предсказания. Кроме того, хранение модели большого порядка требует много памяти.
Если в модели используются для оценки только КМ(N), то иногда такой подход называют "чистым" (pure) контекстным моделированием порядка N. Из-за вышеуказанного недостатка "чистые" модели представляют обычно только научный интерес.
Действительно, реально используемые файлы обычно имеют сравнительно небольшой размер, поэтому для улучшения их сжатия необходимо учитывать оценки вероятностей, получаемые на основании статистики контекстов разных длин. Техника объединения оценок вероятностей, соответствующих отдельным активным контекстам, в одну оценку называется смешиванием (blending). Известно несколько способов выполнения смешивания.
Рассмотрим модель произвольного порядка N. Если  есть вероятность, присваиваемая в активной КМ(o) символу
есть вероятность, присваиваемая в активной КМ(o) символу  алфавита сжимаемого потока, то смешанная вероятность
алфавита сжимаемого потока, то смешанная вероятность  вычисляется в общем случае как
вычисляется в общем случае как

где w(o) - вес оценки КМ(o).
Оценка  обычно определяется через частоту символа
обычно определяется через частоту символа  по тривиальной формуле
по тривиальной формуле

где  - частота появления символа
- частота появления символа  в соответствующем контексте порядка o ;
в соответствующем контексте порядка o ;
 - общая частота появления соответствующего контекста порядка o в обработанной последовательности.
- общая частота появления соответствующего контекста порядка o в обработанной последовательности.
Заметим, что правильнее было бы писать не, скажем,  , а
, а  , т.е. "частота появления символа
, т.е. "частота появления символа  в КМ порядка o с номером j(o) ", поскольку контекстных моделей порядка o может быть огромное количество. Но при сжатии каждого текущего символа мы рассматриваем только одну КМ для каждого порядка, т.к. контекст определяется непосредственно примыкающей слева к символу строкой определенной длины. Иначе говоря, для каждого символа мы имеем набор из N+1 активных контекстов длины от N до 0, каждому из которых однозначно соответствует только одна КМ, если она вообще есть. Поэтому здесь и далее используется сокращенная запись.
в КМ порядка o с номером j(o) ", поскольку контекстных моделей порядка o может быть огромное количество. Но при сжатии каждого текущего символа мы рассматриваем только одну КМ для каждого порядка, т.к. контекст определяется непосредственно примыкающей слева к символу строкой определенной длины. Иначе говоря, для каждого символа мы имеем набор из N+1 активных контекстов длины от N до 0, каждому из которых однозначно соответствует только одна КМ, если она вообще есть. Поэтому здесь и далее используется сокращенная запись.
Если вес w(-1) > 0, то это гарантирует успешность кодирования любого символа входного потока, т.к. наличие КМ(-1) позволяет всегда получать ненулевую оценку вероятности и, соответственно, код конечной длины.
Различают модели с полным смешиванием (fully blended), когда предсказание определяется статистикой КМ всех используемых порядков, и с частичным смешиванием (partially blended) - в противном случае.
