Введение в машинное обучение

1.1.3. Машина опорных векторов

Один из самых популярных методов машинного обучения – машина опорных векторов (SVM – Support Vector Machine) – является развитием идей, предложенных в 1960–1970 гг. В. Н. Вапником и А. Я. Червоненкисом. Окончательное очертание метод принял в 1995 г., когда было показано, как в этом методе можно эффективно использовать ядра [ 4 ].

Рассмотрим вначале случай двух линейно разделимых классов. Для удобства будем их кодировать числами 1, -1, т. е. .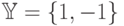

Оптимальной разделяющей гиперплоскостью называется гиперплоскость, такая, что расстояние от нее до ближайшей точки из обучающей выборки (не важно из какого класса) максимально. Таким образом, оптимальная разделяющая гиперплоскость максимизирует зазор (отступ) - расстояние от нее до точек из обучающей выборки. Часто это приводит к хорошим результатам и на объектах тестовой выборки.

Математическая постановка задачи выглядит следующим образом:

Требуется найти

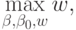
при ограничениях

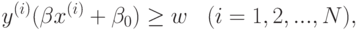
где 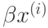означает скалярное произведение

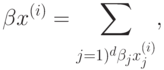
а – евклидову норму

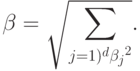
Эквивалентная формулировка:

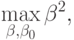
при ограничениях

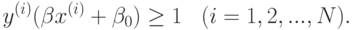
Можно показать, что решение этой задачи имеет вид

уравнение разделяющей гиперплоскости есть 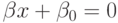и классификатор определяется правилом

Если 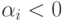, то 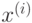называется опорной точкой или опорным вектором. Легко видеть, что опорные точки лежат на границе разделяющей полосы

следовательно, 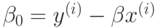, где 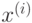- произвольный опорный вектор.

В случае линейно не разделимых классов разрешим некоторым объектам из обучающей выборки "слегка" заходить за разделяющую гиперплоскость:

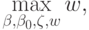
при ограничениях

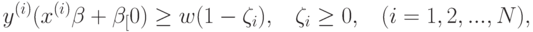
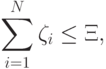
где - некоторая константа (параметр метода). При 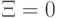получаем предыдущий случай (линейно разделимых классов). Значение 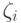пропорционально величине, на которую 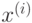заходит за границу разделяющей полосы. В частности, -й объект будет классифицирован неправильно тогда и только тогда, когда 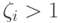. Чем меньше , тем меньше объектов классифицируется неправильно. С другой стороны, должно быть достаточно велико, чтобы задача была совместной.

Эквивалентная формулировка:

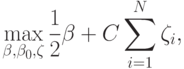
при ограничениях

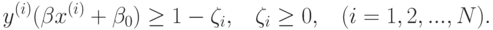
Здесь параметр регулирует величину штрафа за то, что некоторые точки выходят за границу разделяющей полосы. Построенная задача является задачей квадратического программирования. Для ее решения можно использовать общие методы для решения таких задач, однако существуют весьма эффективные специальные методы.

Можно показать, что решение задачи единственно, если в обучающей выборке есть по крайней мере один представитель каждого из классов.

Дальнейшее усовершенствование метода - использование спрямляющих пространств. Пусть удается перейти от исходного пространства признаков к новому пространству (которое называется спрямляющим) с помощью некоторого отображения :

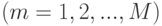где - базисные функции (. Новый классификатор определяется теперь функцией

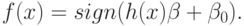
Здесь - разделяющая поверхность. Если отображение подобрано удачно, в новом пространстве классы могут быть линейно разделимы или близки к таковым.

Оказывается, все вычисления при обучении и при расчете функции можно организовать так, что 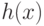встречается только в выражениях вида

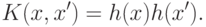
В частности уравнение разделяющей поверхности имеет вид

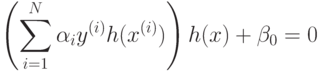
что эквивалентно

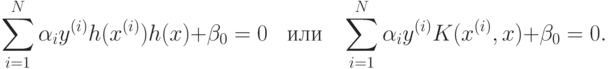
Функция 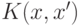называется ядром. На практике, таким образом, вместо того, чтобы испытывать различные функции можно (так и поступают) подбирать наиболее подходящее ядро 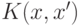. Заметим, что не любая функция 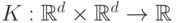представима в виде 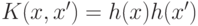, т.е. может быть использована в качестве ядра. Приведем перечень некоторых популярных функций-ядер:

• линейное ядро: ;
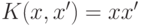• многочлен степени: ;
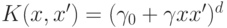• радиальная функция: ;
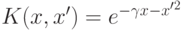• сигмоидальная ("нейронная") функция: .

Для того чтобы использовать метод опорных векторов для задачи классификации с числом классом , возможно использовать две стратегии:

• "Каждый против каждого": построить классификаторов на всех возможных подзадачах бинарной классификации. Новый объект классифицируется всеми построенными решающими правилами, затем выбирается преобладающий класс.
• "Один против всех": обучить моделей на задачах бинарной классификации вида "один класс против всех остальных". Класс нового объекта выбирается по максимальному значению отступа.

1.1.4. Деревья решений

Деревья решений [ 3 ] являются одним из наиболее наглядных и универсальных алгоритмов обучения. К достоинствам деревьев решений следует отнести:

• Возможность производить обучение на исходных данных без их дополнительной предобработки (нормализация и т. п.);
• Нечувствительность к монотонным преобразованиям данных;
• Устойчивость к выбросам;
• Возможность обрабатывать данные с пропущенными значения;
• Поддержка работы с входными переменными разных (смешанных) типов;
• Возможность интерпретации построенного дерева решений.

Кроме того, существуют эффективные алгоритмы их настройки (обучения), например, CART – Classification and Regression Trees [ 3 ] или See5/C5.0.

Основная идея деревьев решений состоит в рекурсивном разбиении пространства признаков с помощью разбиений (splits): гиперплоскостей, параллельных координатным гиперплоскостям (если признак – количественный), либо по категориям (если признак номинальный). В каждом из полученных в конце процедуры "ящиков" 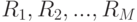функция аппроксимируется константой:

• Для задачи классификации:
  
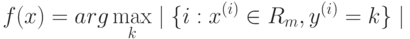
• Для задачи восстановления регрессии:
  

В алгоритме CART разбиения имеют вид:

• , если j-й признак количественный;
• , если j -й признак качественный, 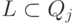, где 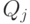- набор значений, которые может принимать j-й признак.

Дерево строится рекурсивно с помощью следующей жадной процедуры, на каждом шаге максимально уменьшая значение функции, описывающей неоднородность данных, содержащихся в узле дерева. Пусть на текущем шаге имеется разбиение пространства признаков на области (ящики)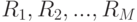

• Выбираем область .
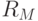• Выбираем и (или ), так, чтобы добиться максимального уменьшения неоднородности, или загрязненности, (impurity) .
• Строим разбиение и повторяем действия.

Разбиения проводятся до тех пор, пока в строящиеся вершины попадает достаточное количество точек обучающей выборки, или пока дерево не достигнет заданной глубины.

Используют различные способы измерить неоднородность, например,

• Для задачи классификации:
  
• Для задачи восстановления регрессии:
  

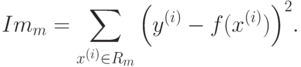
где 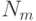- количество точек из обучающей выборки, попавших в область .

Другой важный параметр модели - это глубина дерева решений, регулирующая, "как сильно" будет разбито пространство признаков. Небольшое число разбиений может привести к тому, что построенная модель не будет учитывать некоторые особенности распределения признаков, описывающих те или иные классы, и таким образом приведет к уменьшению точности предсказания. Чрезмерное число разбиений может привести к переобучению модели и снижению её обобщающей способности.

Для того чтобы избежать переобучения, используется процедура отсечений (prunning) [ 3 ].