Имитационное моделирование алгоритма локального голосования для балансировки загрузки узлов вычислительной сети
Цель лабораторной работы

Презентацию к лабораторной работе Вы можете скачать здесь.
Для иллюстрации теоретических результатов приведем пример имитационного моделирования работы алгоритма локального голосования для системы балансировки загруженности узлов децентрализованной вычислительной сети с использование платформы JADE.
Программная реализация сети агентов
В качестве примера рассмотрим вычислительную сеть, состоящую из шести вычислительных узлов. Топология сети в каждый момент времени случайная [ 5.38 ] .
Разработка агентов в JADE похожа на разработку обычных Java-приложений и не требует от программиста специальных технических навыков. Для разработки достаточно иметь Java Development Kit, но для удобства мы использовали традиционную интегрированную среду разработки для Java – Eclipse. Любой агент в системе JADE является классом-наследником класса jade.core.Agent. В наследнике достаточно переопределить метод setup(), в котором агент настраивается для последюущей деятельности.
В первую очередь определяется поведение агента. Мы используем интерфейс CyclicBehaviour, который задает циклическое поведение, необходимое для осуществления итераций. Внутри интерфейса, в методе action(), описывается логика работы с сообщениями, а именно реализуются шаги вычислительной схемы, описанной выше.
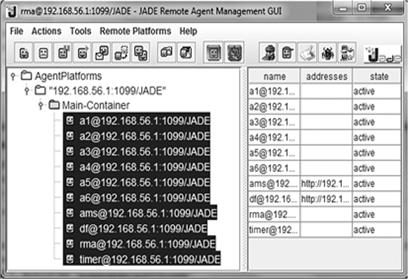
Последующая деятельность агентов, в том числе доставка сообщений между ними, обеспечивается средой JADE. Управление агентами, их запуск и остановку, можно осуществлять через JADE Remote Agent Management GUI. Вывод результатов осуществляется в консоль Eclipse, для этого также можно создать специальное окно ( рис. 10.2).
Для просмотра схемы передачи информации между агентами можно открыть окно Smiffer Agent, в котором стрелками указывается путь передачи единици информации. Рис. 10.3 показывает sniffer agent для примера реализации алгоритма достижения консенсуса, описанного выше.
Созданы шесть агентов с жестко определенной топологией сети, т.е. каждый агент связан только с двумя другими агентами. Агент "timer" подает команду для начала нового цикла обменом информации. Каждый агент начальный момент времени имеет собственное целое число. После применения протокола локального голосования и получения данных от других агентов, он записывает себе новое число и отправляет агенту "timer" сообщение со своим номером о том, что отработал такт. Новый такт не начинается, пока все агенты не "отчитаются" перед агентом "timer". Такт системы равен 1 сек. Для подсчета числа текущего такта агент сравнивает его с числом предыдущего такта. Если число агента не меняется в течении пяти тактов, то агент отправляет на "timer" сообщение об достижении консенсуса. Консенсус достигается при отсутствии изменений числа агента в пределе первого знака дробного числа.
Инструкция по выполнению лабораторной работы
Рассмотрим два случая: стационарный и случай поступлении в тот или иной узел с течением времени новых заданий [39-41].
Для поставленной задачи будем использовать алгоритм стохастической аппроксимации для достижения консенсуса в следующем виде:
 |
( 17) |
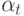 – последовательность положительно определенных размеров шагов.
– последовательность положительно определенных размеров шагов. 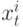 - состояние узла
- состояние узла  в момент времени
в момент времени  ,
, 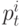 – производительность узла
– производительность узла  .
.
Будем проводить имитационное моделирование для системы, показанной на рис. 10.1, состоящей из 6 вычислительных блоков. Были выбраны начальные состояния загруженности узлов:
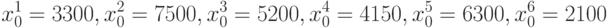
Производительности узлов:

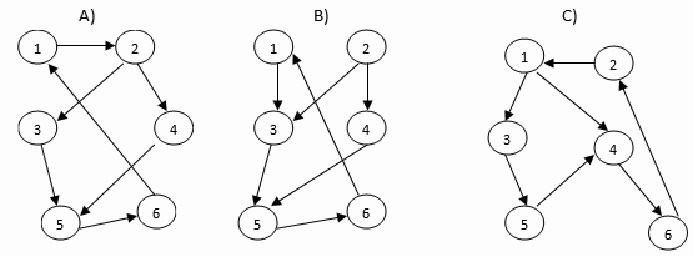
Начальная топология сети приведена на рис. 10.4(А). С течением времени топология сети дважды меняется: рис. 10.4(В) и 5.4(С).
Матрицы связности для трех случаев выглядит так:
 |
( 18) |
- Для простоты сначала рассмотрим стационарный случай – систему, в которой все узлы имеют определенную начальную загрузку, и новые задания не поступают.
График невязки при работе алгоритма (17) для такой системы приведен на рис. 10.5. Система сходится примерно за 75 шагов. Используем коэффициент
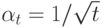 .
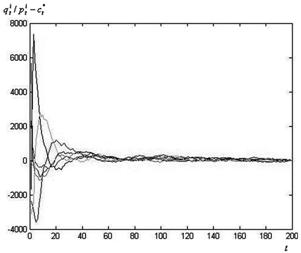
. - Рассмотрим случай, когда в процессе работы алгоритма в систему поступает новый заказ. Используем постоянный размер шага
 . Моделирование этого случая приведено на
рис. 10.6.
. Моделирование этого случая приведено на
рис. 10.6.
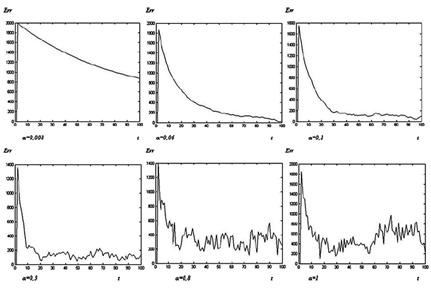
На рис.10.7 приведены графики для величины ошибки оценивания с разными постоянными параметрами шага
 . Ошибка оценивания определяется следующим образом:
. Ошибка оценивания определяется следующим образом: 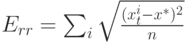 .
.
Видно, что чем больше  , тем состояния узлов быстрее сходятся к консенсусу, но с определенного момента поведение системы перестает быть стабильным.
, тем состояния узлов быстрее сходятся к консенсусу, но с определенного момента поведение системы перестает быть стабильным.
Выводы
В этой главе была рассмотрена задача достижения консенсуса при неполном обмене информацией в условиях переменной топологии. Описан алгоритм стохастической аппроксимации для достижения среднеквадратического консенсуса. Проведено моделирование алгоритма для задачи балансировки загруженности узлов децентрализованной вычислительной сети при поступлении в каждый узел только зашумленной информации о загруженности и производительности соседей, причем топология сети может меняться со временем, а информация от соседей доходить с задержкой во времени.