Мультиагентное управление
Задача консенсуса на графах
Поясним обозначения, использующиеся далее. Верхний индекс  переменных будем используется в качестве индекса, а не показателя степени. Для матрицы
переменных будем используется в качестве индекса, а не показателя степени. Для матрицы  элемент, находящийся на ее
элемент, находящийся на ее  -й строке и в
-й строке и в  -м столбце называется
-м столбце называется  -м элементом и обозначается как
-м элементом и обозначается как  . Для вектора или матрицы
. Для вектора или матрицы  определим норму Фробениуса
определим норму Фробениуса ![\lvert M \rvert=[Tr(M^TM]^{1/2}](/sites/default/files/tex_cache/33ee750fea0536a2245aa83066c5af5f.png) . Будем использовать
. Будем использовать 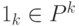 , чтобы определить вектор-столбец из
, чтобы определить вектор-столбец из  единиц. Для вектор-столбцов
единиц. Для вектор-столбцов ![Z_1,...,Z_l,[Z_1;...;Z_l]](/sites/default/files/tex_cache/8b84ad2b48f42d2701d5cc0cfbf06e38.png) определяет вектор-стоблец, полученный вертикальным соединением
определяет вектор-стоблец, полученный вертикальным соединением  векторов.
векторов.
Для описания топологии сети будем использовать понятия теории графов. Ориентированный граф (орграф) 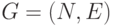 состоит из множества узлов
состоит из множества узлов 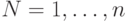 и множества ребер
и множества ребер  . Ребро определяется упорядоченной парой
. Ребро определяется упорядоченной парой 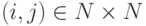 , где
, где 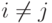 . Направленный путь (из узла
. Направленный путь (из узла 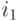 в узел
в узел  ) состоит из последовательности узлов
) состоит из последовательности узлов 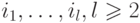 таких, что
таких, что 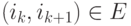 . Орграф
. Орграф  называется сильно связным , если из любого узла в любой другой узел существует направленный путь. Направленное дерево – это орграф, в котором каждый узел
называется сильно связным , если из любого узла в любой другой узел существует направленный путь. Направленное дерево – это орграф, в котором каждый узел  , кроме корня, имеет ровно одного родителя
, кроме корня, имеет ровно одного родителя  , такого, что
, такого, что 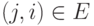 . Будем называть
. Будем называть 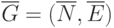 подграфом
подграфом  , если
, если 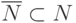 и
и 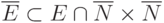 . Будем говорить, что орграф содержит остовное дерево , если существует направленное дерево
. Будем говорить, что орграф содержит остовное дерево , если существует направленное дерево 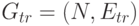 как подграф
как подграф  . Матрицей связности графа
. Матрицей связности графа  называется матрица размером
называется матрица размером  такая, что
такая, что
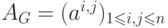 , где
, где 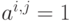 , если
, если  и
и 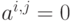 в остальных случаях. Если
в остальных случаях. Если  – неориентированный граф, то каждое ребро определяется как неупорядоченная пара
– неориентированный граф, то каждое ребро определяется как неупорядоченная пара  , где
, где 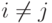 .
.
Топология динамической сети, показывающая принимаемые сигналы моделируется с помощью последовательности орграфов  , где , а каждое
, где , а каждое 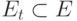 и случайно меняется во времени. Матрица связности
и случайно меняется во времени. Матрица связности  – матрица, которая полностью определяет
– матрица, которая полностью определяет 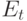 . Если
. Если  , то говорим, что узел
, то говорим, что узел  получает информацию от узла
получает информацию от узла  , который называется соседом узла
, который называется соседом узла  . Обозначим
. Обозначим 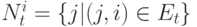 – множеством соседей узла
– множеством соседей узла  . Множество соседей подмножества
. Множество соседей подмножества 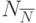 определяется следующим образом:
определяется следующим образом:
 |
( 1) |
Пусть  определяет состояние узла
определяет состояние узла  в момент времени
в момент времени 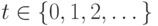 . Определим информационный поток в сети как
. Определим информационный поток в сети как  , где
, где ![X_t=[x^1_t,…,x^n_t],t \geqslant 0](/sites/default/files/tex_cache/c5746cf9e1048874e11d60e6863813e0.png) набор значений состояний узлов сети,
набор значений состояний узлов сети, 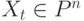 , а
, а 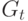 – топология . Состояниями узла могут быть, например, физические характеристики (положение, температура, напряжение и др.). В динамической сети с переменной топологией информационный поток
– топология . Состояниями узла могут быть, например, физические характеристики (положение, температура, напряжение и др.). В динамической сети с переменной топологией информационный поток 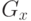 – это дискретное состояние системы, меняющееся во времени. Будем говорить, что узлы
– это дискретное состояние системы, меняющееся во времени. Будем говорить, что узлы  и
и  согласованы в сети тогда и только тогда, когда
согласованы в сети тогда и только тогда, когда 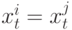 , и узлы достигли консенсуса тогда и только тогда, когда
, и узлы достигли консенсуса тогда и только тогда, когда 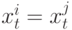 для любых
для любых 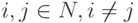 . Когда все узлы сети согласованы, общее значение узлов называется групповым решением .
. Когда все узлы сети согласованы, общее значение узлов называется групповым решением .
Если узлы графа – динамические агенты , описываемые уравнениями:
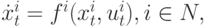 |
( 2) |
то динамический граф(или динамическая сеть) – это динамическая система с состояниями 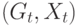 , в которой
, в которой 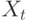 меняется в соответствии с динамикой сети
меняется в соответствии с динамикой сети
![\dot{X}_t=F(X_t,U)=[f^1(x^1_t,u^1_t,...,f^n(x^n_t,u^n_t)]](/sites/default/files/tex_cache/4f30c4b66bd687c2fb91a74520fa8ca7.png) , где
, где ![U=[u^1_t,...,u^n_t]](/sites/default/files/tex_cache/ba0d4f388de5481da9cf35be45aa4a34.png)
Будем считать, что в момент времени  , если
, если  узел
узел  получает, возможно, устаревшую информацию от своих соседей, моделируемую следующим образом:
получает, возможно, устаревшую информацию от своих соседей, моделируемую следующим образом:
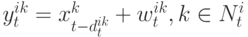 |
( 3) |
где 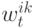 – помехи, а
– помехи, а 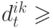 – целочисленная случайная задержка. Так как система начинает работу при
– целочисленная случайная задержка. Так как система начинает работу при 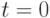 , неявным требованием к множеству соседей будет:
, неявным требованием к множеству соседей будет:
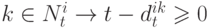 |
( 4) |
Каждый узел использует информацию о своем собственном состоянии (может быть и зашумленную), а также свои зашумленные измерения для 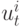 . Будем называть обратную связь по наблюдениям состояний
. Будем называть обратную связь по наблюдениям состояний
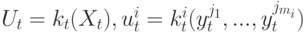 |
( 5) |
протоколом с топологией 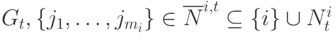 , для любого
, для любого  из узлов
из узлов 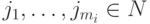 удовлетворяет свойству:
удовлетворяет свойству: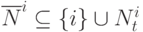 . Если
. Если  <
<  для любого
для любого  , то (5) называется распределенным протоколом .
, то (5) называется распределенным протоколом .
Пусть 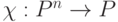 – некоторая функция
– некоторая функция  переменных. Задача
переменных. Задача 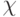 -консенсуса в динамическом графе заключается в распределенном вычислении
-консенсуса в динамическом графе заключается в распределенном вычислении 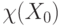 , применяя входы
, применяя входы 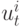 .
.
Определение 1: Протокол (5) асимптотически решает задачу 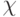 -консенсуса тогда и только тогда, когда существует асимптотически устойчивое равновесие
-консенсуса тогда и только тогда, когда существует асимптотически устойчивое равновесие 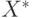 для
для 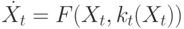 , удовлетворяющее
, удовлетворяющее 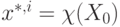 для любого
для любого  .
.
Отметим особые случаи, когда  ,
, 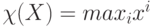 и
и  , называемые консенсус усреднения , -консенсус и -конснсус соответственно 6. Эти случаи широко применяются в распределенных системах принятия решений для мультиагентных систем.
, называемые консенсус усреднения , -консенсус и -конснсус соответственно 6. Эти случаи широко применяются в распределенных системах принятия решений для мультиагентных систем.
Решение задачи консенсуса усреднения является примером распределенного вычисления линейной функции  , используя сеть динамических систем (или интеграторов).
, используя сеть динамических систем (или интеграторов).
Пусть 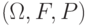 – основное вероятностное пространство и будем считать, что часть или все определенные выше переменные, вектора и матрицы – случайные величины.
– основное вероятностное пространство и будем считать, что часть или все определенные выше переменные, вектора и матрицы – случайные величины.
Обозначим максимальное множество каналов связи  .
.
Для удобства статистического моделирования предположим следующее: 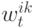 и
и 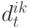 определены для всех
определены для всех  . Если
. Если 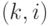 не появляется в
не появляется в 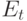 , тогда (3) физически не работает и
, тогда (3) физически не работает и 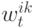 и
и 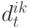 можно считать нулями. Если
можно считать нулями. Если 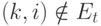 , положим
, положим 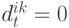 . Пусть
. Пусть 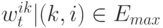 перечислены в определенном порядке
перечислены в определенном порядке 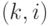 , тогда получаем вектор помех
, тогда получаем вектор помех 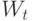 размерности
размерности  .
.
Определение 2:  узлов достигают среднеквадратичного консенсуса , если
узлов достигают среднеквадратичного консенсуса , если  и существует случайная переменная
и существует случайная переменная 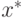 такая что
такая что 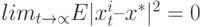 для
для 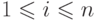 .
.
Далее будет рассмотрен пример мультиагентной системы с описанными выше параметрами.
