Типовые информационные структуры
Решение блочно-двухдиагональной системы определяется рекуррентно:
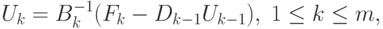
 . Макрооперация
. Макрооперация 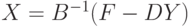 вычисляет
вектор
вычисляет
вектор  по векторам
по векторам  и матрицам
и матрицам  . Построим граф алгоритма,
считая, что каждая из его вершин соответствует данной макрооперации.
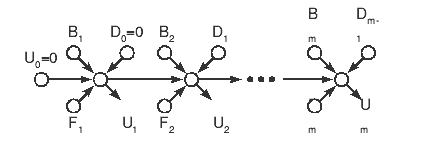
Очевидно, он будет таким, как показано на рис. 9.3. Большие размеры
вершин и дуг на рисунке подчеркивают, что операции являются сложными и
передается сложная информация.
. Построим граф алгоритма,
считая, что каждая из его вершин соответствует данной макрооперации.
Очевидно, он будет таким, как показано на рис. 9.3. Большие размеры
вершин и дуг на рисунке подчеркивают, что операции являются сложными и
передается сложная информация.Из строения графа сразу видно, что если алгоритм рассматривать как последовательность матрично-векторных операций, то он является строго последовательным и не распараллеливается. Практически не распараллеливается и каждая макрооперация в отдельности. Она также представляет решение двухдиагональной системы. Из этих фактов можно было бы сделать вывод о невозможности хорошего распараллеливания алгоритма решения рассматриваемой системы с блочно-двухдиагональной матрицей. Однако такой вывод был бы преждевременным.
Исследуем поэлементную запись алгоритма решения блочно- двухдиагональной системы. С учетом введенных ранее обозначений элементов матриц и векторов имеем:

При этом предполагается, что  для всех
для всех 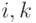 . В этой записи основной и, по существу, единственной является
скалярная операция
. В этой записи основной и, по существу, единственной является
скалярная операция

 по величинам
по величинам 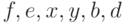 . Для
построения графа алгоритма рассмотрим прямоугольную решетку, узлы
которой имеют целочисленные координаты
. Для
построения графа алгоритма рассмотрим прямоугольную решетку, узлы
которой имеют целочисленные координаты 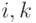 . Во все узлы решетки для
. Во все узлы решетки для  поместим вершины графа и будем считать, что они
соответствуют операции
поместим вершины графа и будем считать, что они
соответствуют операции  . Не будем указывать вершины, поставляющие
входные данные и нулевые значения некоторых аргументов. Анализируя
поэлементную запись, нетрудно убедиться в том, что в вершину с
координатами
. Не будем указывать вершины, поставляющие
входные данные и нулевые значения некоторых аргументов. Анализируя
поэлементную запись, нетрудно убедиться в том, что в вершину с
координатами 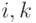 будут передаваться результаты выполнения операций,
соответствующих вершинам с координатами
будут передаваться результаты выполнения операций,
соответствующих вершинам с координатами  и
и  . Вся
остальная информация, необходимая для реализации операции с
координатами
. Вся
остальная информация, необходимая для реализации операции с
координатами 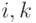 , является входной и нужна для реализации только этой
операции.
, является входной и нужна для реализации только этой
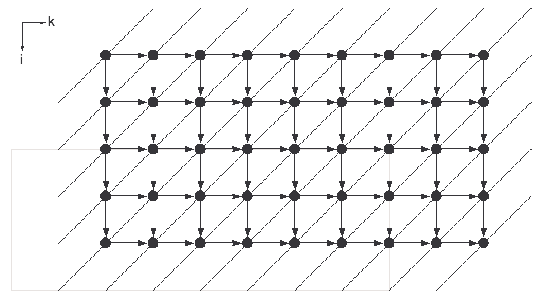
операции.Для случая 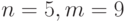 граф алгоритма представлен на рис. 9.4. Из
него следует, что вопреки возможным ожиданиям граф алгоритма прекрасно
распараллеливается. Граф имеет полный набор обобщенных линейных
разверток, в качестве направляющих векторов которых могут быть взяты
координатные векторы. Линейная развертка с направляющим вектором (1,1)
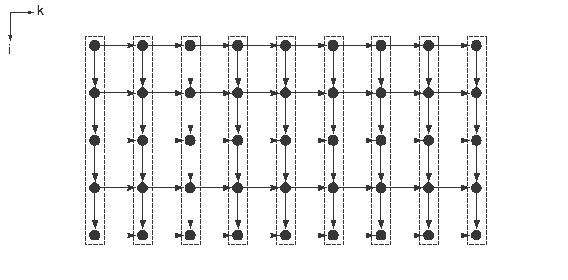
является строгой. На рис. 9.5 в этом же графе пунктирными линиями
обведены группы вершин. Каждая из таких групп соответствует одной
макровершине графа, представленного на рис. 9.3. Из этих рисунков
видно, каким образом хорошо распараллеливаемый алгоритм может
превратиться в нераспараллеливаемый при неудачном укрупнении
операций.
граф алгоритма представлен на рис. 9.4. Из
него следует, что вопреки возможным ожиданиям граф алгоритма прекрасно
распараллеливается. Граф имеет полный набор обобщенных линейных
разверток, в качестве направляющих векторов которых могут быть взяты
координатные векторы. Линейная развертка с направляющим вектором (1,1)
является строгой. На рис. 9.5 в этом же графе пунктирными линиями
обведены группы вершин. Каждая из таких групп соответствует одной
макровершине графа, представленного на рис. 9.3. Из этих рисунков
видно, каким образом хорошо распараллеливаемый алгоритм может
превратиться в нераспараллеливаемый при неудачном укрупнении
операций.
Явная схема для уравнения теплопроводности. Рассмотрим далее
решение краевой задачи для одномерного уравнения теплопроводности.
Пусть требуется найти решение  , где
, где

Построим равномерную сетку с шагом  no
no  и шагом
и шагом  по
по  .
Предположим, что по тем или иным причинам выбора выбрана явная схема
.
Предположим, что по тем или иным причинам выбора выбрана явная схема
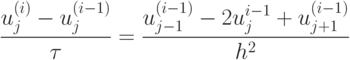

 . Переменные
. Переменные 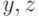 связаны с переменными
связаны с переменными  соотношениями
соотношениями

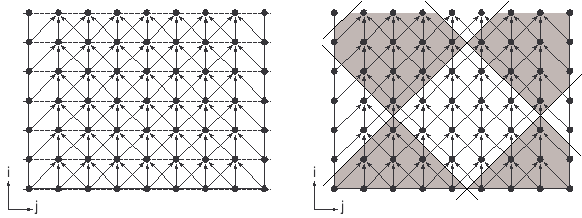
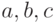 . Для случая
. Для случая  граф алгоритма представлен на обоих
рисунках 9.6. На
границе области расположены вершины, символизирующие ввод начальных
данных и граничных значений. Граф имеет полный набор обобщенных
линейных разверток. В качестве их направляющих векторов в системе
координат
граф алгоритма представлен на обоих
рисунках 9.6. На
границе области расположены вершины, символизирующие ввод начальных
данных и граничных значений. Граф имеет полный набор обобщенных
линейных разверток. В качестве их направляющих векторов в системе
координат  могут быть взяты, например, векторы (1,1) и (1,-1).
Имеются и строгие линейные развертки. Одна из них задается
направляющим вектором (1,0).
могут быть взяты, например, векторы (1,1) и (1,-1).
Имеются и строгие линейные развертки. Одна из них задается
направляющим вектором (1,0).Операции одного яруса этой развертки не зависят друг от друга и их можно реализовывать на разных устройствах одновременно. Но эффективность такой организации параллельных вычислений может оказаться очень низкой. На рис. 9.6 слева пунктирными линиями показаны ярусы максимальной параллельной формы алгоритма. Предположим, что операции реализуются по этим ярусам. Каждая операция одного яруса требует трех аргументов. Они являются результатами выполнения операций на предыдущем ярусе. Если данные, полученные на одном ярусе, могут быстро извлекаться из памяти, то никаких серьезных проблем с реализацией алгоритма по ярусам параллельной формы не возникает. Однако для больших многомерных задач ярусы оказываются столь масштабными, что информация о них может не поместиться в одной быстрой памяти. Тогда для ее размещения приходится использовать либо медленную, либо распределенную память. Для этих видов памяти время выборки одного числа может существенно превышать время выполнения базовой операции. Это означает, что при переходе к очередному ярусу время, затраченное на выполнение операций, может оказаться значительно меньше времени взаимодействия с памятью. Чем меньше отношение времени выполнения операций к времени доступа к памяти, тем меньше эффективность реализации алгоритма по ярусам параллельной формы. В этом случае большая часть времени работы параллельного компьютера будет тратиться на осуществление обменов с памятью, а не на собственно счет.
Ранее уже отмечалось, что знание двух и более обобщенных разверток позволяет перейти от микроописания алгоритма к его макроописанию. Такой переход показан на рис. 9.6 справа. Поверхности уровней обобщенных разверток разбивают область задания графа на многогранники. Исходный алгоритм теперь можно реализовывать по полученным многогранникам, в том числе, параллельно. При этом одному процессору всегда поручается выполнение всех операций, относящихся к одному многограннику. При параллельной реализации сначала выполняются операции, соответствующие нижним заштрихованным многогранникам на правом рис. 9.6. Затем параллельно выполняются операции, соответствующие соседним незаштрихованным многогранникам и т. д.
В новом процессе операции одного многогранника становятся макрооперацией. Время выполнения макрооперации определяется числом вершин в многограннике, что примерно пропорционально его площади. Информационную связь между собой многогранники осуществляют через вершины, лежащие около границ. Следовательно, время на извлечение из памяти информации, необходимой для реализации макрооперации, определяется длиной границы многогранника. Размеры многогранников можно выбрать произвольно. Они зависят только от того, какие ярусы обобщенных параллельных форм формируют их границы. Всегда можно выбрать такое разбиение области задания графа, при котором для большинства многогранников отношение длин границ к их площадям будет сколь угодно малым. При реализации таких макроопераций влияние времени доступа к медленной памяти будет снижено очень сильно.
Метод Жордана. Рассмотрим решение системы линейных алгебраических уравнений методом Жордана без выбора ведущего элемента. Этот метод можно записать многими различными способами. Пусть, например, он записан так:

Будем считать, что  . Расположим опорные многогранники
операторов 1-3, 5 вокруг опорного многогранника оператора 4. Область,
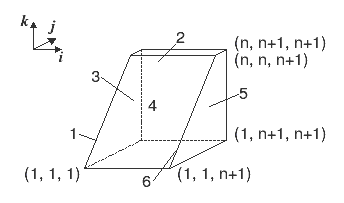
занимаемая вершинами графа алгоритма, изображена на рис. 9.7.
. Расположим опорные многогранники
операторов 1-3, 5 вокруг опорного многогранника оператора 4. Область,
занимаемая вершинами графа алгоритма, изображена на рис. 9.7.
Она представляет усеченную пирамиду, из которой исключено ребро 6. Вершины опорного многогранника 1 расположены на ребре 1, многогранника 2 - на грани 2, многогранника 3 - на грани 3, многогранника 5 - на грани 5, вершины опорного многогранника 4 расположены в остальной части пирамиды. Основной объем вычислений приходится на оператор 4, который является телом тройного цикла. Неоднородности вычислений, связанные с операторами 1 - 3, 5, локализованы на границе. Структура связей в графе показана на рис. 9.8.
Граф является регулярным. В каждую его вершину входят и выходят
дуги, определяемые векторами (1, 0, -1), (0, 1, 0), (0, 0, 1) в
системе координат  . Рассылка элементов
. Рассылка элементов 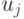 осуществляется вдоль
прямых, параллельных оси
осуществляется вдоль
прямых, параллельных оси  . Она начинается на грани 3 и заканчивается
на грани 5, проходя через соответствующие точки пирамиды. Рассылка
элементов
. Она начинается на грани 3 и заканчивается
на грани 5, проходя через соответствующие точки пирамиды. Рассылка
элементов  начинается на грани 2 и ребре 1 и проходит через
соответствующие точки пирамиды на прямых,
параллельных оси
начинается на грани 2 и ребре 1 и проходит через
соответствующие точки пирамиды на прямых,
параллельных оси  . При этом полагается, что
. При этом полагается, что  совпадает с
совпадает с  . Входные
данные алгоритма, т.е. элементы матрицы и правой части, поступают
через нижнюю грань. Граф имеет полный набор обобщенных линейных
разверток. В качестве их направляющих векторов в системе координат
. Входные
данные алгоритма, т.е. элементы матрицы и правой части, поступают
через нижнюю грань. Граф имеет полный набор обобщенных линейных
разверток. В качестве их направляющих векторов в системе координат  могут быть взяты, например, векторы (1, 0, 0), (1, 0, 1) и (0, 1, 0).
Имеются и строгие линейные развертки. Одна из них задается
направляющим вектором (2, 1, 1).
могут быть взяты, например, векторы (1, 0, 0), (1, 0, 1) и (0, 1, 0).
Имеются и строгие линейные развертки. Одна из них задается
направляющим вектором (2, 1, 1).
Заметим, что в отличие от других графов описанная укладка графа для метода Жордана появилась далеко не сразу. Пришлось перепробовать много вариантов, прежде чем удалось найти столь красивое расположение графа. Возможно, что у графа каждого отработанного и хорошо изученного алгоритма можно найти какие-то изящные укладки. Вот только обнаружить их очень не просто. Тем не менее, кажется, что их поиск достоин большего внимания. Ведь наличие каталога красиво уложенных графов типовых алгоритмов имело бы большое значение как для теории, так и для практики.