Параллельные вычисления и математическое образование

Известно, что освоение вычислительной техники параллельной архитектуры, в особенности молодыми специалистами, идет с большими трудностями. На наш взгляд, это связано с тем, что знакомство с параллельными вычислениями, как и образование в этой области в целом, начинается не с того, с чего надо бы начинать. К тому же то, с чего надо начинать, не рассказывается ни в каких курсах вообще.

Возможность быстрого решения задач на вычислительной технике параллельной архитектуры вынуждает пользователей изменять весь привычный стиль взаимодействия с компьютерами. По сравнению, например, с персональными компьютерами и рабочими станциями меняется практически все: применяются другие языки программирования, видоизменяется большинство алгоритмов, от пользователей требуется предоставление многочисленных нестандартных и трудно добываемых характеристик решаемых задач, интерфейс перестает быть дружественным и т.п. Важным является то обстоятельство, что неполнота учета новых условий работы может в значительной мере снизить эффективность использования новой и, к тому же, достаточно дорогой техники.

Надо заметить, что общий характер трудностей, сопровождающих развитие параллельных вычислений, в целом выглядит таким же, каким он был и во времена последовательных. Только для параллельных вычислений все трудности проявляются в более острой форме. Во многом из-за большей сложности самой предметной области. Но, возможно, главным образом вследствие того, что к началу активного внедрения вычислительных систем параллельной архитектуры в практику решения больших прикладных задач не был построен нужный теоретический фундамент и не был развит математический аппарат исследований. В конце концов, из-за этого оказался своевременно не подготовленным весь образовательный цикл в области параллельных вычислений, отголоски чего проявляются до сих пор. Отсюда непонимание многочисленных трудностей освоения современной вычислительной техники, пробелы в подготовке нужных специалистов и многое другое.

Образование в области параллельных вычислений базируется на трех дисциплинах: архитектура вычислительных систем, программирование и вычислительная математика. Если внимательно проанализировать содержание соответствующих курсов, то неизбежно приходить к выводу, что не только по отдельности, но даже все вместе они не обеспечивают в настоящее время достижение главной пользовательской цели - научиться эффективно решать большие задачи на больших вычислительных системах параллельной архитектуры. Конечно, в этих курсах дается немало полезных и нужных сведений. Однако многое, что необходимо знать согласно современному взгляду на параллельные вычисления, в них не дается. Это, в частности, связано с тем, что ряд важнейших и даже основополагающих фактов, методов и технологий решения больших задач на больших системах возник как результат исследований на стыке нескольких предметных областей. Такие результаты не укладываются в рамки традиционных дисциплин. Поэтому, как следствие, излагаемые в соответствующих курсах сведения оказываются недостаточными для формирования целостной системы знаний, ориентированной на грамотное построение параллельных вычислительных процессов.

Все образовательные курсы, так или иначе связанные с вычислительной техникой или ее использованием, можно разделить на две группы. В первой группе излагаются базовые сведения, во второй - специальные. Базовые сведения носят универсальный характер и слабо классифицируются по типам вычислительной техники. Сформировались они на основе знаний о последовательных машинах и последовательных вычислениях и с течением времени меняются мало. В рамках курса по программированию базовые сведения начинают читаться с первого или второго семестра, в рамках курса по численным методам примерно с третьего семестра. Специальные курсы, в том числе относящиеся к вычислительным системам параллельной архитектуры, начинают читаться довольно поздно. Как правило, не ранее седьмого или даже девятого семестра.

На первый взгляд, все выглядит логично: сначала даются базовые сведения, затем специальные. Однако на практике разделение сведений на базовые и специальные оказывается весьма условным, поскольку важно только следующее: есть ли возможность получить нужные сведения в нужный момент или такой возможности нет и каков набор предлагаемых к изучению сведений.

Становление вычислительной математики имеет долгую историю. Но наиболее бурное ее развитие связано с электронными вычислительными машинами. Эти машины возникли как инструмент проведения последовательных вычислений. Интенсивно развиваясь, они по существу оставались последовательными в течение нескольких десятилетий. Для последовательных машин довольно рано стали создаваться машинно-независимые языки программирования. Для математиков и разработчиков прикладного программного обеспечения появление таких языков открывало заманчивую перспективу. Не нужно было вникать в устройство вычислительных машин, так как языки программирования по существу мало чем отличались от языка математических описаний. Скорость реализации алгоритмов на последовательных машинах определялась, главным образом, числом выполняемых операций и почти не зависела от того, как внутренне устроены сами алгоритмы. Поэтому в разработке алгоритмов становились очевидными главные целевые функции их качества - минимизация числа выполняемых операций и устойчивость к влиянию ошибок округления. Никакие другие сведения об алгоритмах были просто не нужны для эффективного решения задач на последовательной технике.

Все это на долгие годы определило основное направление развития не только численных методов, но и всей вычислительной математики. На фоне недостаточного внимания к развитию вычислительной техники математиками не было вовремя замечено важное обстоятельство: количественные изменения в технике переходят уже в такие качественные, что общение с ней при помощи последовательных языков скоро должно стать невозможным. Это привело к серьезному разрыву между имеющимися знаниями в области алгоритмов и теми знаниями, которые необходимы для быстрого решения задач на новейшей вычислительной технике. Образовавшийся разрыв лежит в основе многих трудностей практического освоения современных вычислительных систем параллельной архитектуры.

Сейчас вычислительный мир, по крайней мере, мир больших вычислений изменился радикально. Он стал параллельным. На вычислительных системах параллельной архитектуры время решения задач принципиально зависит от того, какова внутренняя структура алгоритма и в каком порядке выполняются его операции. Возможность ускоренной реализации на параллельных системах достигается за счет того, что в них имеется достаточно большое число функциональных устройств, которые могут одновременно выполнять какие-то операции алгоритма. Но чтобы использовать эту возможность, необходимо получить новые сведения относительно структуры алгоритма на уровне связей между отдельными операциями. Более того, эти сведения нужно согласовывать со сведениями об архитектуре вычислительной системы.

О совместном анализе архитектуры систем и структуры алгоритмов почти ничего не говорится в образовательных курсах. Если об архитектурах вычислительных систем и параллельном программировании рассказывается хотя бы в специальных курсах, то обсуждение структур алгоритмов на уровне отдельных операций в настоящее время не входит ни в какие образовательные дисциплины. И это несмотря на то, что структуры алгоритмов обсуждаются в научной литературе в течение нескольких десятилетий, да и практика использования вычислительной техники параллельной архитектуры насчитывает не намного меньший период. Естественно, возник вопрос о том, что же делать дальше. Ответ на него уже был дан раньше, но его полезно и повторить.

До сих пор специалистов в области вычислительной математики учили, как решать задачи математически правильно. Теперь надо, к тому же, учить, как решать задачи эффективно на современной вычислительной технике.

О том, какие сведения в области структуры алгоритмов необходимо знать дополнительно, говорилось в приведенных лекциях. На основе этого материала можно разработать разные программы модернизации образовательных курсов в интересах параллельных вычислений. Наиболее эффективная модернизация связана с проведением согласованных изменений нескольких курсов. Одна из программ, рассчитанная на подготовку высококвалифицированных специалистов по решению больших задач на больших системах, может выглядеть следующим образом:

• чтение на первых курсах трех-четырех лекций "Введение в параллельные вычисления";
• введение в базовые циклы по математике и программированию начальных сведений о параллельных вычислениях;
• существенная перестройка цикла лекций по численным методам с обязательным описанием информационной структуры каждого алгоритма;
• организация практикума по параллельным вычислениям;
• чтение специального курса "Параллельная структура алгоритмов";
• чтение специального курса "Параллельные вычисления".

Эта программа в определенном смысле максимальная. Тем не менее, она вполне реальная. Безусловно, ее нельзя целиком реализовать в каждом вузе. Но на ее основе для каждого конкретного вуза можно сформировать свою собственную программу образования в области вычислительных наук.

Из первых двух пунктов в образовательный цикл можно вводить как любой из них, так и оба сразу. Важно лишь, чтобы обучающийся как можно раньше узнал, что существуют другие способы организации вычислительных процессов, а не только последовательное выполнение "операция за операцией", что на этих других способах строится самая мощная современная вычислительная техника, что только на такой технике удается решать крупные промышленные и научные задачи и т.д. Важно, в первую очередь, для того, чтобы как можно раньше обратить внимание обучающихся на необходимость критического отношения к философии последовательных вычислений. Ведь именно с этой философией им приходится сталкиваться на протяжении всего образования как в школе, так и в вузе. И именно эта философия мешает пониманию особенностей работы на вычислительной технике параллельной архитектуры.

Начальные сведения о параллельных вычислениях вполне уместно включить в курс программирования. В нем можно обсудить простейшую модель параллельной вычислительной системы, рассказать о параллельных процессах и их характеристиках. Здесь же полезно ввести абстрактную форму описания вычислительных алгоритмов. Причем совсем не обязательно приводить конкретные ее наполнения. Об этом лучше поговорить позднее при изучении численных методов. Можно начать разговор о параллельных формах алгоритмов и их использовании. Все сведения о параллельных вычислениях, на наш взгляд, можно изложить в курсе программирования в двух-трех лекциях. Хорошим полигоном для демонстрации параллелизма в алгоритмах является курс линейной алгебры. В нем достаточно рано появляются матричные операции и метод Гаусса для решения систем линейных алгебраических уравнений. На соответствующих алгоритмах даже "на пальцах" можно продемонстрировать и параллелизм вычислений, и быстрые алгоритмы и многое другое. На обсуждение новых сведений потребуется суммарно не более одной лекции.

Не стоит перегружать первое знакомство с параллельными вычислениями большим количеством деталей и серьезными результатами. Главная цель данного этапа - лишь вызвать интерес к этой тематике. Достаточно дать общее представление о параллелизме вычислений, параллельных формах, графах алгоритмов и характеристиках вычислительных процессов. Если все начальные сведения объединить в единый цикл "Введение в параллельные вычисления", то их можно рассказать за три-четыре лекции. Но подчеркнем еще раз - доводить эти сведения до обучающихся необходимо как можно раньше.

Материалы данных лекций убедительно демонстрируют, насколько важно хорошее знание графов алгоритмов и их параллельных форм для понимания тех проблем, с которыми приходится сталкиваться при решении задач на современных вычислительных системах параллельной архитектуры. Изложение сведений об этом наиболее естественно включить в курсы по вычислительной математике. Основной аргумент в пользу такого решения связан с тем, что информационная структура алгоритмов описывается в тех же самых индексных системах, в которых происходит изложение и численных методов. По большому счету, к существующему курсу численных методов нужно добавить только сведения о графах алгоритмов, наборах разверток для них и технологию использования всего этого. Безусловно, подготовка обновленных курсов требует определенного труда. Но совсем не обязательно обсуждать структуры алгоритмов в полном изложении. Достаточно это сделать лишь для их вычислительных ядер. Понятие о графах алгоритмов и технологию нужно изложить, скорее всего, в самом начале курса. Однако граф и развертки желательно давать для каждого алгоритма. В дополнение к сказанному заметим, что одни и те же численные методы читаются без изменения в течение многих лет, а сведения об их структурах нужно подготовить только один раз. И эти сведения заведомо будут использоваться многократно, причем в самых разных областях.

Одним из самых трудных в техническом отношении и менее всего проработанным с методологической точки зрения является вопрос об организации практикума по параллельным вычислениям. Конечно, для его проведения нужно иметь вычислительную технику параллельной архитектуры. Но во многих вузах такая техника уже давно стоит, а окончательного мнения, каким должен быть практикум, тем не менее, все равно нет.

Одна из очевидных целей практикума лежит на поверхности. Вычислительные системы параллельной архитектуры создаются для решения больших задач. Следовательно, за время прохождения практикума нужно хотя бы в какой-то мере научиться решать такие задачи. Вроде бы все ясно. В общем курсе программирования или в каких-то специальных курсах даются знания по конкретным языкам или системам параллельного программирования. Во время практикума раздаются конкретные задания. Программы составляются, пропускаются на вычислительной системе и результаты сравниваются с эталоном. Однако даже в такой простой схеме имеются узкие места. В самом деле, что считать результатом? При решении больших задач на больших системах основную трудность представляет не столько получение математически правильного результата, сколько достижение нужного уровня ускорения. А это означает, что во время прохождения практикума нужно ко всему прочему научиться правильно оценивать эффективность составленных программ.

Если конкретная программа не показывает нужных характеристик эффективности, то возникает вопрос о дальнейших действиях. В этой ситуации почти всегда приходится приступать к более детальному изучению структуры алгоритмов. Возможно, именно изучение структуры алгоритмов должно стать ключевым звеном практикума. Оно стало бы хорошим подспорьем знакомству со структурой алгоритмов в модернизированных курсах по численным методам. Но есть и более веские аргументы в пользу более близкого знакомства со структурой алгоритмов.

Один из аргументов связан с текущими проблемами. В последнее время в практике вычислений стали широко использоваться различные многопроцессорные системы с распределенной памятью. К ним относятся не только кластеры, но и неоднородные сети компьютеров, сети компьютеров, объединенных через Интернет, и др. Во всех подобных системах узким местом являются обмены информацией между процессорами. Для эффективной работы необходимо, чтобы каждый процессор выполнял достаточно много операций и обменивался с памятью других процессоров относительно небольшими порциями данных. Мы уже отмечали в лекциях, что для обеспечения такого режима счета, достаточно знать граф алгоритма и, по крайней мере, две независимые развертки. Другими словами, нужно знать структуру алгоритмов.

Другой аргумент связан с возможной перспективой развития вычислительной техники. Скорости решения больших задач приходится повышать сегодня и заведомо придется повышать в будущем. Как правило, основные надежды связываются с созданием на основе различных технологических достижений более скоростных универсальных систем. Но повышать скорость работы вычислительной техники можно и за счет ее специализации. Уже давно практикуется использование спецпроцессоров, осуществляющих очень быструю реализацию алгоритмов быстрого преобразования Фурье, обработки сигналов, матричных операций и т.п. А теперь вспомним гипотезу о типовых структурах. Если она верна, то в конкретных прикладных областях можно будет выделить наиболее часто используемые алгоритмы и для них тоже построить спецпроцессоры. Тем самым открывается путь создания специализированных вычислительных систем для быстрого и сверхбыстрого решения задач из заданной предметной области.

Основная трудность введения в практикум заданий, связанных с изучением структуры алгоритмов, является отсутствие в настоящий момент доступного и простого в использовании программного обеспечения для построения графов алгоритмов и проведения на их основе различных исследований. По существу есть только одна система, которая реализует подобные функции. Это система V-Ray, разработанная в Научно- исследовательском вычислительном центре МГУ. Она дает возможность для различных классов программ строить графы алгоритмов и изучать их параллельную структуру. Система V-Ray реализована на персональном компьютере и не зависит от целевого компьютера. Последнее обстоятельство исключительно важно для организации практикума, поскольку частый выход с мелкими задачами на большие вычислительные системы не очень реален даже для вузов с хорошим техническим оснащением. На персональных же компьютерах время освоения задач практикума практически неограниченно. В настоящее время V-Ray представляет сложную исследовательскую систему. Далеко не все ее функции нужны для организации практикума. Со временем система V-Ray станет доступной для широкого использования. Информацию о ней и ее возможностях можно получить по адресу http://v-ray.parallel.ru.

Рис. 10.1. Компьютеры и структура алгоритмов

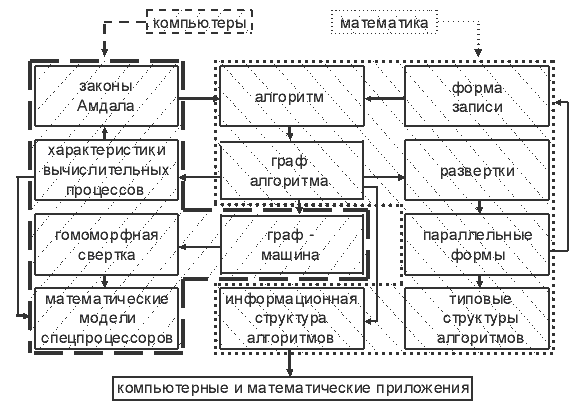
Что касается содержания специальных курсов, то оно полностью определяется задачами, которые стоят перед конкретным образованием. Нужный материал может быть взят из настоящих лекций, из книги [ 1 ] или из любых других подходящих источников. На наш взгляд, очень важно показать, насколько тесно переплетаются между собой процессы развития вычислительных систем и изучения структуры алгоритмов. Некоторые из таких связей отражены на приведенной выше схеме.