Компьютеры и параллельные формы алгоритмов
Быстрое развитие элементной базы привело к тому, что уже в начале 60-х годов прошлого столетия стали серийно выпускаться вычислительные системы, в которых насчитывалось порядка десятка процессоров, работающих параллельно. Создателям компиляторов все еще удавалось прикрывать пользователей от такого параллелизма, и язык общения оставался практически последовательным. В конце 70-х годов появились серийные вычислительные машины векторного типа, в которых ускорение достигалось за счет быстрого выполнения операций над векторами. Уровень внутреннего параллелизма в них был достаточно высок, хотя весьма специального вида. Создатели компиляторов снова попытались сделать язык программирования последовательным. И на этот раз потерпели неудачу. Формально все еще оставалась возможность пользоваться некоторым последовательным языком. Но заложенная в компилятор технология автоматического выявления векторных конструкций из текста программ оказалась не эффективной. Поэтому, если пользователя не устраивала скорость работы откомпилированной программы, ему нужно было просматривать служебную информацию о работе компилятора и на основе ее анализа самому находить узкие места компиляции и вручную перестраивать программу под векторные конструкции. О том, как именно это делать, конструктивных советов не предлагалось. На практике процедуру перестройки программ приходилось делать многократно.
По существу на этом закончился период, когда задачу, полностью описанную на последовательном языке, можно было более или менее эффективно решать на любой вычислительной технике. На этом же стало заканчиваться время создания классических последовательных компьютеров и началась эра параллельных компьютеров и больших вычислительных систем параллельной архитектуры. По сравнению с последовательными компьютерами в них все обстоит иначе. Рядовые их представители имеют десятки процессоров, а самые большие - десятки и даже сотни тысяч. Мощности параллельных компьютеров огромны и теоретически не ограничены. Практические скорости уже сегодня достигают сотен триллионов операций в секунду. Однако все эти преимущества имеют серьезную негативную сторону: в отличие от последовательных компьютеров использовать параллельные чрезвычайно трудно, интерфейс с ними оказывается совсем не дружественным, языки программирования перестали быть универсальными, от пользователя требуется много новой и трудно доступной информации о структуре алгоритмов и т.д.
На вычислительных системах параллельной архитектуры время решения задач решающим образом зависит от того, какова внутренняя структура алгоритма и в каком порядке выполняются его операции. Возможность ускоренной реализации алгоритма на параллельных системах достигается за счет того, что в них имеется достаточно большое число процессоров, которые могут параллельно выполнять операции алгоритма. Предположим для простоты, что все процессоры имеют одинаковую производительность и работают в синхронном режиме. Тогда общий коэффициент ускорения по сравнению с тем случаем, когда алгоритм реализуется на одном универсальном процессоре такой же производительности, оказывается примерно равным числу операций алгоритма, выполняемых в среднем на всех процессорах в каждый момент времени. Если параллельные вычислительные системы имеют десятки и сотни тысяч процессоров, то отсюда никак не следует, что при решении конкретных задач всегда можно и, тем более, достаточно легко получить ускорение счета такого же порядка.
На любой вычислительной технике одновременно могут выполняться только независимые операции. Это означает следующее. Пусть снова все процессоры имеют одинаковую производительность и работают в синхронном режиме. Допустим, что в какой-то момент времени на каких-то процессорах выполняются какие-то операции алгоритма. Результат ни одной из них не только не может быть аргументом любой из выполняемых операций, но даже не может никаким косвенным образом оказывать влияние на их аргументы. Если рассмотреть процесс реализации алгоритма во времени, то в силу сказанного сам процесс на любой вычислительной системе, последовательной или параллельной, разделяет операции алгоритма на группы. Все операции каждой группы независимы и выполняются одновременно, а сами группы реализуются во времени последовательно одна за другой. Это неявно порождает некоторую специальную форму представления алгоритма, в которой фиксируются как группы операций, так и их последовательность. Называется она параллельной формой алгоритма [ 1 ] . Ясно, что при наличии в алгоритме ветвлений или условных передач управления его параллельная форма может зависеть от значений входных данных.
Параллельную форму алгоритма можно ввести и как эквивалентный математический объект, не зависящий от вычислительных систем. Зафиксируем входные данные и разделим все операции алгоритма на группы. Назовем их ярусами и пусть они обладают следующими свойствами. Во-первых, в каждом ярусе находятся только независимые операции. И, во-вторых, существует такая последовательная нумерация ярусов, что каждая операция из любого яруса использует в качестве аргументов либо результаты выполнения операций из ярусов с меньшими номерами, либо входные данные алгоритма. Ясно, что все операции, находящиеся в ярусе с наименьшим номером, всегда используют в качестве аргументов только входные данные. Будем считать в дальнейшем, что нумерация ярусов всегда осуществляется с помощью натуральных чисел подряд, начиная с 1.
Число операций в ярусе принято называть шириной яруса, число ярусов в параллельной форме - высотой параллельной формы. Очевидно, что ярусы математической параллельной формы являются не чем иным как теми самыми группами, о которых говорилось выше. При одних и тех же значениях входных данных между математическими параллельными формами алгоритма и реализациями того же алгоритма на конкретных или гипотетических вычислительных системах с одним или несколькими процессорами существует взаимно однозначное соответствие. Если какая-то параллельная форма отражает реализацию алгоритма на некоторой вычислительной системе, то ширина ярусов говорит о числе используемых в каждый момент времени независимых устройств, а высота - о времени реализации алгоритма.
Каждый алгоритм при фиксированных входных данных в общем случае имеет много параллельных форм. Формы, в которых все ярусы имеют ширину, равную 1, существуют всегда. Все они отражают последовательные вычисления и имеют максимально большие высоты, равные числу выполняемых алгоритмом операций. Даже таких параллельных форм алгоритм может иметь несколько, если он допускает различные эквивалентные реализации. Наибольший интерес представляют параллельные формы минимальной высоты, так как именно они показывают, насколько быстро может быть реализован алгоритм, по крайней мере, теоретически. По этой причине минимальная высота всех параллельных форм алгоритма называется высотой алгоритма. Существует параллельная форма, в которой каждая операция из яруса с номером k, k >1, получает в качестве одного из аргументов результат выполнения некоторой операции из ( k -1)-го яруса. Такая параллельная форма называется канонической. Для любого алгоритма при заданных входных данных каноническая форма всегда существует, единственна и имеет минимальную высоту. Кроме этого, в канонической параллельной форме, как и в любой другой форме минимальной высоты, ярусы в среднем имеют максимально возможную ширину [ 1 ] . Таким образом, решая любую задачу на любой вычислительной системе с развитым параллелизмом на уровне функциональных устройств, пользователь неизбежно, явно или неявно, соприкасается с параллельной формой реализуемого алгоритма. И это происходит даже тогда, когда он ничего не знает обо всех этих понятиях. Если не сам пользователь или разработчик программы, то кто-то другой или что-то другое, например, компилятор, операционная система, какая-нибудь сервисная программа, а скорее всего все они вместе, закладывают в вычислительную систему некоторую программу действий, что и порождает соответствующую им параллельную форму.
А теперь вспомним, что достигаемое ускорение в среднем пропорционально числу операций, выполняемых в каждый момент времени. Если оно равно общему числу имеющихся процессоров, то данный алгоритм при заданных входных данных реализуется на используемой вычислительной системе эффективно. В этом случае возможный ресурс ускорения использован полностью и более быстрого счета достичь на выбранной системе невозможно ни практически, ни теоретически. Но если ускорение значительно меньше числа устройств?
Предположим, что оно существенно меньше средней ширины ярусов канонической параллельной формы реализуемого алгоритма. Это означает, что не очень удачно выбрана схема реализации алгоритма. Изменив ее, можно попытаться более полно использовать имеющийся потенциал параллелизма в алгоритме. Заметим, что в практике общения с параллельными компьютерами именно эта ситуация возникает наиболее часто. Если же ускорение равно средней ширине ярусов канонической параллельной формы, то весь потенциал параллелизма в алгоритме выбран полностью. В данном случае никаким изменением схемы счета нельзя использовать большее число устройств системы и, следовательно, нельзя добиться большего ускорения. И, наконец, вполне возможно, что даже при использовании всех процессоров реальное ускорение не соответствует ожидаемому. Это означает, что при реализации алгоритма приходится осуществлять какие-то передачи данных, требующие длительного времени. Для того чтобы теперь понять причины замедления, необходимо особенно тщательно изучить структуру алгоритма и/или вычислительной системы. В практике общения с параллельными компьютерами эта ситуация также возникает достаточно часто.
Таким образом, как только возникает необходимость решать какие-то вопросы, связанные с анализом ускорения при решении задачи на вычислительной системе параллельной архитектуры, так обязательно требуется получить какие-то сведения относительно структуры алгоритма на уровне связей между отдельными операциями. Более того, чаще всего эти сведения приходится сопоставлять со сведениями об архитектуре вычислительной системы. Проведение совместного анализа представляет сложный процесс, но о нем почти ничего не говорится в образовательных курсах. Понятно, почему это происходит. Если об архитектурах вычислительных систем и параллельном программировании рассказывается хотя бы в специальных курсах, то обсуждение структур алгоритмов на уровне отдельных операций в настоящее время не входит ни в какие образовательные дисциплины. И это несмотря на то, что структуры алгоритмов обсуждаются в научной литературе в течение нескольких десятилетий, да и практика использования вычислительной техники параллельной архитектуры насчитывает не намного меньший период.
Отсутствие нужных сведений о структуре алгоритмов не могло остановить развитие собственно вычислительной техники. Стали создаваться новые языки и системы программирования, в огромном количестве и самого различного типа: от расширения последовательных языков параллельными конструкциями до создания на макроуровне параллельных языков типа автокода [ 1 ] .
Очевидно, что разработчики компиляторов и средств программирования, так же как и конструктора вычислительной техники, не могут сказать что-либо существенное о структуре выполняемых алгоритмов. Но они хорошо понимают, какие множества операций на той или иной технике будут эффективно реализовываться в режиме параллельного счета. Поэтому во всех новых языках и системах программирования стали вводиться конструкции, позволяющие описывать такие множества. А вот ответственность за поиск в алгоритмах этих множеств и их описание соответствующими конструкциями языка была возложена на разработчиков программ. Как следствие, на них же перекладывалась и ответственность за эффективность функционирования создаваемого ими программного продукта. Конечно, в таких условиях даже не шла речь о какой-либо преемственности программ. Главными проблемами пользователей стали нахождение многочисленных и трудно добываемых характеристик решаемых задач и организация параллельных вычислительных процессов. Вычислительным сообществом это рассматривается как неизбежная плата за возможность быстро решать задачи. Но во всем сообществе расплачиваются, главным образом, пользователи, постоянно переписывая свои программы.
Невнимание со стороны математиков к развитию вычислительной техники привело к серьезному разрыву между имеющимися знаниями в области алгоритмов и теми знаниями, которые были необходимы для быстрого решения задач на новейшей вычислительной технике. Образовавшийся разрыв сказывается до сих пор, и именно он лежит в основе многих трудностей практического освоения современных вычислительных систем параллельной архитектуры.
До сих пор специалистов в области вычислительной математики учили, как решать задачи математически правильно. Теперь надо, к тому же, учить, как решать задачи эффективно на современной вычислительной технике. А это совсем другая наука, математическая по своей сути, но которую пока почти не изучают в вузах.
Для успешного решения задач на вычислительных системах параллельной архитектуры приходится привлекать принципиально новые сведения о структуре алгоритмов на уровне связей отдельных операций между собой. В первую очередь, необходимо знать множества операций, которые можно выполнять независимо. Другими словами, нужны сведения как раз о тех параллельных формах алгоритмов, о которых говорилось выше.
Для большей наглядности проведенных рассуждений всюду выше явно или неявно предполагалось, что все процессоры вычислительной системы работают в синхронном режиме и выполняют любую операцию за одно и то же время. Такое предположение не принципиально по сути дела. Но оно позволяет более отчетливо показать смысл введения параллельных форм как очень важных объектов, описывающих тонкие структурные свойства и характеристики алгоритмов. Оказалось, что эти объекты удобно задавать ориентированными графами.
В самом деле, во всех рассуждениях не имело никакого значения, какие именно операции выполняют процессоры. Они могли быть и простейшими машинными операциями, и сколь угодно большими совокупностями операций, оформленными в виде функций, подпрограмм или программных комплексов. Будем считать операции алгоритма вершинами графа. На множестве вершин-операций естественным образом определен частичный порядок, показывающий, какие операции вслед за какими могут выполняться. Этот же порядок позволяет задать дуги графа. Если операция, соответствующая вершине В, использует в качестве хотя бы одного своего аргумента результат выполнения операции, соответствующей вершине А, то проведем дугу из вершины А в вершину В. В противном случае дуга между вершинами А и В не проводится. Проделаем то же самое для каждой пары вершин. Тем самым будет построен ориентированный ациклический граф. Он называется графом алгоритма.
Граф алгоритма играет исключительно важную роль в изучении
параллельных свойств самого алгоритма. Его значение определяется двумя
факторами. Во-первых, он устроен значительно проще самого алгоритма,
так как не связан ни с какой атрибутикой, сопровождающей описание
алгоритма. Граф алгоритма можно рассматривать как классический
математический объект и ничто не мешает исследовать его чисто
математическими методами. И, во-вторых, по графу алгоритма очень
просто строить параллельные формы. Действительно, выберем какое-то
число не связанных дугами вершин, которые, в свою очередь, не имеют
входящих дуг (независимых операций алгоритма, аргументами которых
являются только входные данные алгоритма). Будем считать их первым
ярусом параллельной формы. Предположим, что уже построено 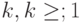 ярусов параллельной формы. Выберем любое число не связанных дугами
вершин, в которые могут входить дуги только из вершин первых k ярусов
(независимых операций алгоритма, аргументами которых являются либо
входные данные алгоритма, либо результаты выполнения операций,
соответствующих первым k ярусам). Будем считать их ( k +1)-ым ярусом
параллельной формы. Продолжим процесс до тех пор, пока не будут
исчерпаны все вершины графа. В результате всех таких действий будет
построена параллельная форма графа алгоритма.
ярусов параллельной формы. Выберем любое число не связанных дугами
вершин, в которые могут входить дуги только из вершин первых k ярусов
(независимых операций алгоритма, аргументами которых являются либо
входные данные алгоритма, либо результаты выполнения операций,
соответствующих первым k ярусам). Будем считать их ( k +1)-ым ярусом
параллельной формы. Продолжим процесс до тех пор, пока не будут
исчерпаны все вершины графа. В результате всех таких действий будет
построена параллельная форма графа алгоритма.
Очевидно, что понятия параллельной формы для алгоритма или его графа изоморфны. Следовательно, с точки зрения изучения параллелизма в алгоритмах безразлично, с какими из этих форм иметь дело. В дальнейшем терминологию и свойства, относящиеся к параллельным формам алгоритма, без дополнительных оговорок будем переносить на граф алгоритма. И наоборот.
Как уже отмечалось, граф алгоритма устроен существенно проще, чем сам алгоритм. Поэтому намечается следующая линия действий: сначала находится граф алгоритма, затем изучаются подходящие его параллельные формы и, наконец, на основе проведенных исследований выбирается нужная схема реализации алгоритма на вычислительной системе параллельной архитектуры. Но возникает очень много вопросов, касающихся, в первую очередь того, как строить и изучать графы алгоритмов. Ответы на них будут даны позднее.
Перспектива внедрения в практику параллельных вычислительных систем потребовала разработки математической концепции построения параллельных алгоритмов, т.е. алгоритмов, специально приспособленных для реализации на подобных системах. Такая концепция необходима для того, чтобы научиться понимать, как следует конструировать параллельные алгоритмы, что можно ожидать от них в перспективе и какие подводные камни могут встретиться на этом пути. Концепция начала активно развиваться в конце 50-х - начале 60-х годов прошлого столетия и получила название концепции неограниченного параллелизма.
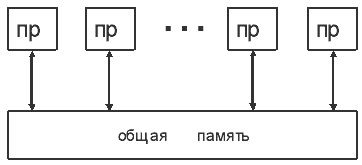
Истоки этого названия связаны с выбором для нее абстрактной модели параллельной вычислительной системы. Поскольку концепция разрабатывалась для проведения математических исследований, то в требованиях к модели могло присутствовать самое минимальное число технических параметров. Тем более что в то время о структуре параллельных вычислительных систем и путях их совершенствования было вообще мало что известно. Лишь быстрое развитие элементной базы подсказывало, что число процессоров в системе вскоре может стать очень большим. Но что-нибудь другое спрогнозировать было трудно. Поэтому явно или неявно в модели остались только следующие предположения. Число процессоров может быть сколь угодно большим, все они работают в синхронном режиме и за единицу времени выполняют абсолютно точно любую операцию из заданного множества. Процессоры имеют общую память. Все вспомогательные операции, взаимодействие с памятью, управление компьютером и любые передачи информации осуществляются мгновенно и без конфликтов. Входные данные перед началом вычислений записаны в память. Каждый процессор считывает свои операнды из памяти и после выполнения операции записывает результат в память. После окончания вычислительного процесса все результаты остаются в памяти.
Для математических исследований нет особого смысла усложнять модель параллельной вычислительной системы. Математикам приходится изучать различные алгоритмы, в том числе весьма экзотические, если их рассматривать с позиций возможной реализации на существующей вычислительной технике. Но какой будет вычислительная техника завтра и, тем более, послезавтра - неизвестно. Одна из схем абстрактной модели параллельной вычислительной системы представлена на рис.3.2.
Несмотря на то, что концепция неограниченного параллелизма предельно проста, она вполне приемлема для первого знакомства с параллельными вычислениями. Более того, именно в силу своей простоты она оказалась очень живучей и до сих пор используется для иллюстрации различных свойств алгоритмов. Например, на ней легко демонстрируются параллельные формы алгоритмов, показывается зависимость ширины ярусов, числа задействованных процессоров и получаемого ускорения. Если бы концепция неограниченного параллелизма не нужна была ни для чего другого, ее все равно следовало бы создать. Просто из-за того, что параллельные формы являются одним из важнейших инструментов изучения структуры алгоритмов.