Большие задачи и большие компьютеры
Интересно отметить, что даже там, где натурные эксперименты являются привычным инструментом исследования, большие вычислительные системы начинают активно использоваться. Рассмотрим, например, проблему компоновки летательного аппарата, обладающего минимальным лобовым сопротивлением, максимально возможными значениями аэродинамического качества и допустимого коэффициента подъемной силы при благоприятных характеристиках устойчивости и управляемости в эксплуатационных режимах. Для ее решения традиционно использовались продувки отдельных деталей аппарата или его макета в аэродинамических трубах. Но вот несколько цифр. При создании в начале века самолета братьев Райт эксперименты в аэродинамических трубах обошлись в несколько десятков тысяч долларов, бомбардировщик 40-х гг. потребовал миллион, а корабль многоразового пользования "Шатл" - 100 млн. долларов. Столь же сильно возрастает время продувки в расчете на одну трубу - почти 10 лет для современного аэробуса. Однако несмотря на огромные денежные и временные затраты, продувки в аэродинамических трубах не дают полной картины обтекания хотя бы просто потому, что обдуваемый образец нельзя окружить датчиками во всех точках. Для преодоления этих трудностей также пришлось обратиться к численным экспериментам с математической моделью.
Определять аэродинамические характеристики летательного аппарата необходимо уже на стадии проектирования. Необходимо также давать оценку различным вариантам компоновки, оптимизировать геометрические параметры, определять внешний облик с наилучшими характеристиками. Знание соответствующих данных нужно и в процессе летных испытаний при анализе их результатов для выработки рекомендаций по устранению выявленных недостатков. Эта задача не может быть решена без информации об обтекании элементов аппарата и поле течения в целом. Как уже говорилось экспериментальное получение такой информации по мере усложнения летательных аппаратов становится все более труднодоступным делом.
В практике работы конструкторских организаций используются инженерные методы расчета, основанные на упрощенных математических моделях. Эти методы пригодны на самых ранних этапах проектирования. Они не могут учесть деталей течения, необходимых на углубленных этапах проектирования, и не могут обеспечить требуемую точность расчетов. В большой области изменения физических параметров упрощенные модели вообще не применимы. Для углубленной стадии проектирования летательных аппаратов перспективными являются математические модели, основанные на нестационарных пространственных уравнениях динамики невязкого, нетеплопроводного газа, в том числе, учитывающие уравнения состояния и уравнения вязкого пограничного слоя между поверхностью аппарата и обтекаемой средой. Модели принципиально различаются для случаев сверхзвукового и дозвукового набегающего потока. Вообще говоря, случай дозвукового обтекания сложнее, так как около летательного аппарата возможно образование местных сверхзвуковых зон. Все части аппарата здесь взаимно влияют друг на друга и задача должна решаться глобально, т. е. во всей области, окружающей летательный аппарат. Именно для расчета дозвуковых течений необходимо использовать вычислительные системы высокой производительности с большим объемом памяти.
Приведем некоторые данные конкретного расчета. Рассчитывались различные варианты дозвукового обтекания летательного аппарата сложной конструкции. Математическая модель требует задания граничных условий на бесконечности. Реально, конечно, область исследования берется конечной. Однако из-за обратного влияния границы ее удаление от объекта должно быть значительным по всем направлениям. На практике это составляет десятки длин размера аппарата. Таким образом, область исследования оказывается трехмерной и весьма большой. При построении алгоритмов нахождения численных решений опять используется принцип дискретизации. Из-за сложной конфигурации летательного аппарата разбиение выбирается очень неоднородным. Общее число элементов, на которые разбивается область, определяется сеткой с числом шагов порядка 102 по каждому измерению, т. е. всего будет порядка 106 элементов. В каждой точке надо знать 5 величин. Следовательно, на одном временном слое число неизвестных будет равно 5x106. Для изучения нестационарного режима приходится искать решения в 102-104 слоях по времени. Поэтому одних только значимых результатов промежуточных вычислений необходимо найти около 109-1011. Для получения каждого из них и дальнейшей его обработки нужно выполнить 102-103 арифметических операций. И это только для одного варианта компоновки и режима обтекания. А всего требуется провести расчеты для десятков вариантов. Приближенные оценки показывают, что общее число операций для решения задачи обтекания летательного аппарата в рамках современной модели составляет величину 1015-1016. Для достижения реального времени выполнения таких расчетов быстродействие вычислительной системы должно быть не менее 109-1010 арифметических операций с плавающей запятой в секунду при оперативной памяти не менее 109 слов.
Успехи в численном решении задач обтекания позволили создать комбинированную технологию разработки летательных аппаратов. Теперь основные эксперименты, особенно на начальной стадии проектирования, проводятся с математической моделью. Они позволяют достаточно достоверно определить оптимальную компоновку, проанализировать все стадии процесса обтекания, выявить потенциально опасные режимы полета и многое другое. Все это дает возможность снизить до минимума дорогостоящие натурные эксперименты в аэродинамических трубах и сделать их более целенаправленными. Конечно, численные эксперименты на высокопроизводительных вычислительных системах тоже обходятся недешево. Но все же они значительно дешевле, чем натурные эксперименты. Кроме этого, их стоимость постоянно снижается. Например, по данным США она уменьшается в 10 раз каждые 10 лет. Объединение численных и натурных экспериментов в единый технологический процесс привело к принципиально новому уровню аэродинамического проектирования. В результате значительно возросло качество, уменьшились стоимость, сроки проектирования и время испытаний летательных аппаратов. Совершенствование математических моделей сделает этот процесс еще более эффективным. Как и в примере с климатом, более совершенные модели потребуют применения более мощных вычислительных систем. В свою очередь, появление новых систем опять даст толчок совершенствованию моделей и т. д. Снова убеждаемся в том, что большие задачи и большие вычислительные системы с точки зрения их развития оказывают влияние друг на друга.
В рассмотренной проблеме выбора компоновки летательного аппарата легко увидеть нечто большее, имеющее отношение к самым различным областям деятельности человека. В самом деле, при создании тех или иных изделий, механизмов и сооружений, также как и при проведении многих научных экспериментов весь процесс от возникновения идеи до ее реализации можно грубо разбить на следующие этапы. Сначала каким-то способом разрабатывается общий проект и готовится технологическая документация. Затем строится опытный образец или его макет. И, наконец, проводится испытание. По его результатам в опытный образец вносятся изменения и снова проводится испытание. Цикл образец - испытание - образец повторяется до тех пор, пока опытный образец не станет действующим, удовлетворяя всем заложенным в проект требованиям. Проведение каждого испытания и внесение очередных изменений в опытный образец почти всегда требует много денег и много времени. Поэтому одна из общих задач заключается в том, чтобы на пути превращения опытного образца в действующий сократить до минимума как число испытаний, так и их стоимость и время проведения. По существу это можно сделать единственным способом — заменить часть натурных экспериментов или большинство из них, а в идеале даже все, экспериментами с математическими моделями. Значимость численных экспериментов в общем процессе зависит от качества модели. Если она хорошо отражает создаваемый или изучаемый объект, натурные эксперименты оказываются необходимыми достаточно редко, что, в свою очередь, приводит к большим материальным и временным выгодам. В этой ситуации весь процесс во многом превращается в своего рода компьютерную игру, в которой можно посмотреть различные варианты решений, обнаружить и исследовать узкие места, выбрать оптимальный вариант, проанализировать последствия такого выбора и т. д. И лишь изредка отдельные решения придется проверять на натурных экспериментах. Это обстоятельство, безусловно, стимулирует создание самых совершенных математических моделей в различных областях.
Очевидно, что использование математических моделей невозможно без применения вычислительной техники. Но оказывается, что для очень многих случаев нужна не просто какая-нибудь техника, а именно высокопроизводительная. В самом деле, изучаем ли мы процесс добычи нефти, или прочность кузова автомобиля, или процессы преобразования электрической энергии в больших трансформаторах и т. п., - исследуемые объекты являются трехмерными. Чтобы получить приемлемую точность численного решения объект нужно покрыть сеткой не менее чем 100x100x100 узлов. В каждой точке сетки нужно определить 5-20 функций. Если изучается нестационарное поведение объекта, то состояние всего ансамбля значений функций нужно определить в 102-104 моментах времени. Поэтому только значимых результатов промежуточных вычислений для подобных объектов нужно получить порядка 109-1011. Теперь надо принять во внимание, что на вычисление и обработку каждого из промежуточных результатов, как показывает практика, требуется в среднем выполнить 102-103 арифметических операций. И вот мы уже видим, что для проведения только одного варианта численного эксперимента число операций порядка 1011-1014 является вполне рядовым. А теперь учтите число вариантов, накладные расходы на время решения задачи, появляющиеся за счет качества программирования, компиляции и работы операционной системы. И сразу становится ясно, что скорость вычислительной техники должна измеряться многими миллиардами и даже триллионами операций в секунду. Такая техника стоит недешево. Тем не менее, как говорится, игра стоит свеч.
Мы неоднократно подчеркивали влияние больших задач на развитие вычислительной техники и наоборот. Постепенно в эту сферу втягивается много чего другого. Развитие математического моделирования приводит к более сложным описаниям моделей. Для их осмысления и разработки принципов исследования приходится привлекать новейшие достижения из самых разных областей математики. Дискретизация задач приводит к системам уравнений с огромным числом неизвестных. Прежние методы их решения не всегда оказываются пригодными по соображениям точности, скорости, требуемой памяти, структуре алгоритмов и т. п. Возникают и реализуются новые идеи в области вычислительной математики. В конечном счете, для более совершенных математических моделей создаются новые методы реализации численных экспериментов. Как правило, они требуют больших вычислительных затрат и снова не хватает вычислительных мощностей. А далее опять все идет по кругу, о чем уже не один раз говорилось выше.
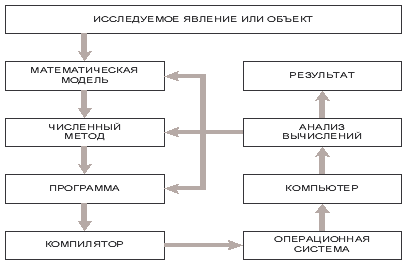
Решаясь на регулярное использование больших численных экспериментов, приходится заботиться о качестве их проведения. Оно определяется многими факторами. Основные этапы, которые проходит каждый эксперимент, отражены на рис. 1.1 Данным рисунком мы хотим подчеркнуть простую мысль: если хотя бы один из этапов, изображенных на рис. 1.1 окажется не эффективным, то не эффективным будет и весь численный эксперимент.
Следовательно, внимательному изучению должны подвергаться все этапы численного эксперимента. Эффективность этапов, связанных с выбором численного метода и составлением программы, в значительной мере определяется пользователем. Однако работа компилятора, операционной системы и самого компьютера ему не подвластна. Тем не менее, имеется возможность повысить эффективность и этих этапов. Связана она с выбором подходящих форм алгоритма и программы, поскольку разные программы показывают разную эффективность. Принимая во внимание особенности конкретной вычислительной системы, можно попытаться найти подходящий вариант программы. Вопрос состоит только в том, на основе каких знаний осуществлять данный выбор. Все эти обстоятельства важно понять, запомнить и постоянно учитывать на практике.