Предварительные сведения
Графы
Мы часто сталкиваемся с задачами, в условиях которых заданы некоторые объекты и между некоторыми их парами имеются определенные связи. Если объекты изобразить точками ( вершинами ), а связи - линиями ( ребрами ), соединяющими соответствующие пары точек, то получится рисунок, называемый графом. Приведем основные определения.
Граф (ориентированный) - это пара
, где
- конечное множество вершин (узлов, точек) графа, а
- некоторое множество пар вершин, т.е. подмножество множества
или бинарное отношение на
. Элементы
называют ребрами (дугами, стрелками, связями). Для ребра
вершина
называется началом
, а вершина
- концом
, говорят, что ребро
ведет из
в
.
В графе полустепень исхода вершины - это число исходящих из нее ребер, а полустепень захода - это число входящих в данную вершину ребер.
Заметим, что в графе может быть ребро вида  , называемое петлей.
, называемое петлей.
Пример 1.3. На рис. 1.1 приведен пример графа  .
Здесь
.
Здесь  ,
В графе
,
В графе 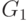 ребро
ребро 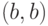 является петлей,
полустепень исхода вершины
является петлей,
полустепень исхода вершины  равна 2, а полустепень захода для нее
равна 1.
равна 2, а полустепень захода для нее
равна 1.
Во многих приложениях с вершинами и ребрами графов связывается некоторая дополнительная информация. Обычно она представляется с помощью функций разметки вершин и ребер.
Определение 1.6.
Размеченный граф - это граф
, снабженный одной или двумя функциями разметки вида:
и
, где
и
- множества меток вершин и ребер, соответственно.
Упорядоченный граф - это размеченный граф
, в котором ребра, выходящие из каждой вершины
, упорядочены, т.е. помечены номерами
, где
- полустепень исхода
, т.е.
.
Упорядоченный граф с полустепенью исхода вершин
называется бинарным.
В качестве множества меток ребер  часто выступают числа,
задающие "веса", "длины", "стоимости" ребер. Графы с такой разметкой
часто называют взвешенными.
часто выступают числа,
задающие "веса", "длины", "стоимости" ребер. Графы с такой разметкой
часто называют взвешенными.
Часто на одном множестве объектов определено несколько различных бинарных отношений. Для представления такой ситуации служат мультиграфы.
Определение 1.7. Мультиграф  состоит из
конечного множества вершин
состоит из
конечного множества вершин  и мультимножества ребер
и мультимножества ребер  , состоящего из пар вершин
, состоящего из пар вершин  , в которое эти пары могут входить по
нескольку раз.
, в которое эти пары могут входить по
нескольку раз.
Обычно несколько ребер, соединяющих одну и ту же пару вершин, различаются метками - именами соответствующих бинарных отношений. В лекциях 4-6 мультиграфы будут использоваться для представления диаграмм конечных автоматов.
Во многих случаях естественно не различать графы, отличающиеся лишь именами (порядком) вершин.
Определение 1.8. Изоморфизм графов. Два графа
и
называются изоморфными, если между их вершинами существует взаимно однозначное соответствие
такое, что для любой пары вершин
из
ребро
ребро
.
Для изоморфизма размеченных графов требуется также совпадение меток соответствующих вершин:
и/или ребер:
.
Многие приложения графов связаны с изучением путей между их вершинами.
Определение 1.9.
Путь в ( мульти ) графе - это последовательность ребер вида
. Этот путь ведет из начальной вершины
в конечную вершину
и имеет длину
. В этом случае будем говорить, что
достижима из
. Будем считать, что каждая вершина достижима сама из себя путем длины 0. Путь в графе (не мультиграфе!) можно также определять как соответствующую последовательность вершин:
, где
при
.
Путь назывется простым, если все ребра и все вершины на нем, кроме, быть может, первой и последней, различны.
Циклом в графе называется путь, в котором начальная вершина совпадает с конечной и который содержит хотя бы одно ребро. Цикл
называется простым, если в нем нет одинаковых вершин, кроме первой и последней, т.е. если все вершины
различны.
Следующее утверждение непосредственно следует из определений.
Лемма 1.1.Если в графе
имеется путь из вершины
в вершину
, то в нем имеется и простой путь из
в
.

