Упорядоченные бинарные диаграммы решений (УБДР)
Рассматриваемый в этой лекции способ представления булевых функций с помощью специального подкласса ориентированных графов без циклов был предложен Р. Бриантом (R. Bryant) в 1986г. Его английское название - "Ordered binary decision diagram", сокращенно - OBDD. Сейчас УБДР являются одним из основных средств реализации булевых функций от большого числа переменных в задачах искусственного интеллекта, проверки правильности электронных схем, программ, протоколов и т.п.
Основные определения
Одним из предшественников УБДР являются бинарные деревья решений.
Определение 3.1. Бинарное дерево решений (БДР) - это бинарное дерево T=(V,E), все внутренние вершины которого помечены переменными, а листья - значениями 0 или 1. Из каждой внутренней вершины v выходят 2 ребра, одно помечено 0, другое - 1; вершина w0, в которую ведет ребро, помеченное 0, называется 0-сыном v, а вершина w1, в которую ведет ребро, помеченное 1, называется 1-сыном v.
Такое дерево, вершины которого помечены переменными x1, ..., xn реализует булеву
функцию f(x1, ..., xn), если для каждого набора значений переменных  ветвь в дереве, соответствующая этому набору
(из вершины xi идем по ребру, помеченному
ветвь в дереве, соответствующая этому набору
(из вершины xi идем по ребру, помеченному 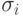 ), завершается листом
с меткой
), завершается листом
с меткой 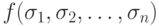 .
.
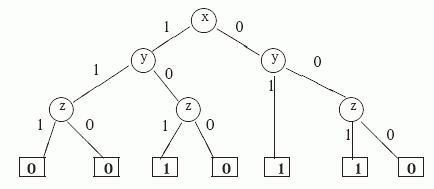
Пример 3.1. Например, рассмотрим изображенное ниже БДР T1 (на всех рисунках предполагается, что ребра направлены сверху вниз).
По определению T1 реализует функцию f1(x,y,z), представленную в таблице 3.1.
| x | y | z | f(x,y,z) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1. | 1 | 0 |
Нетрудно построить ДНФ этой функции: 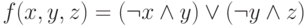 .
.
УБДР являются модификацией БДР, в которой все листья с одной меткой представлены одной вершиной, в каждую вершину может входить несколько ребер, возможен выбор порядка появления переменных на ветвях.
Определение 3.2. Пусть зафиксирован некоторый порядок n переменных 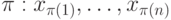 .
.
Упорядоченная бинарная диаграмма решений относительно порядка
переменных  - это ориентированный граф без циклов с одним корнем, в котором
- это ориентированный граф без циклов с одним корнем, в котором
- существует лишь две вершины, из которых не выходят ребра; они помечены константами 0 и 1 и называются стоками ;
- остальные ( внутренние ) вершины помечены переменными и из каждой из них выходят два ребра, одно помечено 0, другое - 1;
- порядок, в котором переменные встречаются на любом пути из корня в сток, совместим с
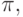 т.е. если из вершины, помеченной
т.е. если из вершины, помеченной 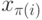 , есть путь в вершину, помеченную
, есть путь в вершину, помеченную 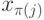 , то i < j.
, то i < j.
Как и в случае БДР, УБДР реализует булеву функцию f(x1, ..., xn), если для каждого набора значений переменных  путь в диаграмме, начинающийся в корне и соответствующий этому набору
(из вершины xi идем по ребру, помеченному
путь в диаграмме, начинающийся в корне и соответствующий этому набору
(из вершины xi идем по ребру, помеченному 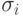 ), завершается стоком
с меткой
), завершается стоком
с меткой 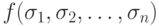 .
.
Из этого определения непосредственно следует, что каждая внутренняя вершина
диаграммы v, помеченная переменной  , является корнем
поддиаграммы, которая включает все вершины диаграммы,
достижимые из v, и реализует некоторую функцию
, является корнем
поддиаграммы, которая включает все вершины диаграммы,
достижимые из v, и реализует некоторую функцию  от (n -k +1) переменных
от (n -k +1) переменных 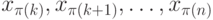 . При этом ее
0-сын w0 является корнем поддиаграммы, реализующей функцию
. При этом ее
0-сын w0 является корнем поддиаграммы, реализующей функцию  , а
1-сын w1 - корень поддиаграммы, реализующей функцию
, а
1-сын w1 - корень поддиаграммы, реализующей функцию  .
Пусть диаграмма реализует функцию
.
Пусть диаграмма реализует функцию 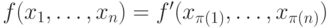 и
и 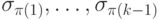 - это набор значений переменных
- это набор значений переменных 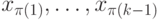 , который соответствует пути из корня в вершину v (таких наборов может быть несколько).
Тогда
, который соответствует пути из корня в вершину v (таких наборов может быть несколько).
Тогда  .
.
Пример 3.2. Реализуем с помощью УБДР функцию f1(x,y,z), представленную выше в примере 3.1, с помощью БДР T1 и таблицы 3.1.
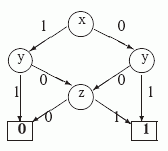
Вначале зафиксируем порядок переменных: x < y < z. Объединив листья с одинаковыми метками и две z - вершины с одинаковыми потомками, получим УБДР D1, приведенную на рис.3.2.
Ясно, что реализация функции f1(x,y,z) с помощью УБДР D1 намного компактнее, чем с помощью БДР T1.
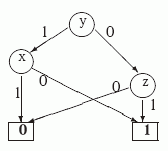
Под сложностью L(D) УБДР D будем понимать число внутренних вершин в D. Например, L(D1)=4. Может ли сложность диаграммы для некоторой функции зависеть от порядка переменных? Да! Рассмотрим порядок переменных y < x < z. Как показывает следующий рисунок, относительно этого порядка функцию f(x,y,z) можно реализовать УБДР D2 со сложностью L(D2)=3.