Линейная зависимость векторов. Размерность и базис линейного пространства. Линейные операции в координатах

Линейные операции в координатах

В "лекции 4" , уже рассматривались линейные операции над векторами, такие как сложение, вычитание и умножение. Эти операции определяются следующей теоремой.

Теорема. При умножении вектора на число каждая из его координат умножается на это число, а при сложении складываются соответствующие координаты.

Доказательство. Пусть даны два произвольных вектора x и y и некоторое произвольное число . Разложим векторы по базису l₁, l₂, ..., l_n, получим x=x₁l₁+x₂l₂+...+x_nl_n и y=y₁l₁+y₂l₂+...+y_nl_n и найдем произведение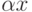

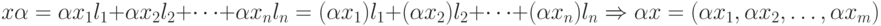
и сумму x + y

x+y = (x1l1+x2l2+...+xnln)+(y1l1+y2l2+...+ynln)=
=(x1+y1)l1+(x2+y2)l2+...+(xn+yn)ln =>
=> x+y = [(x1+y1);(x2+y2);...;(xn+yn)].

Доказанная теорема очень важна в математике, так как из нее следует признак линейной зависимости и независимости векторов. Покажем это. Пусть в некотором n -мерном пространстве R задана система векторов:

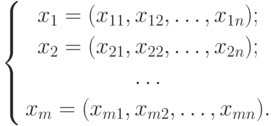( 8.5)

Умножим каждый из векторов на некоторое число 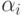и сложим их все друг с другом. В результате получим линейную комбинацию этих же векторов, которая является новым вектором, равным, по определению 12, нулю

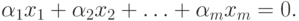( 8.6)

Распишем систему (8.6) в координатной форме

( 8.7)

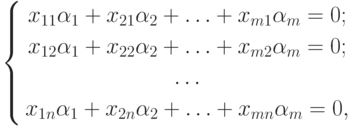( 8.8)

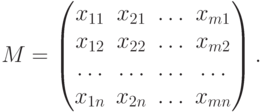( 8.9)

Равенство (8.7) эквивалентно равенствам (8.6) и (8.8). На основании теоремы можно утверждать, что векторы системы (8.5) линейно независимы тогда и только тогда, когда однородная система (8.8) имеет единственное нулевое решение, что на практике обозначает, что ранг матрицы (8.9) равен количеству векторов системы m.