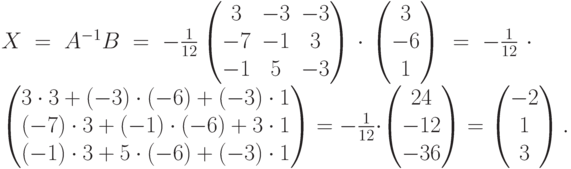НОУ ИНТУИТ | Введение в линейную алгебру. Лекция 5: Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.10.2007 | Доступ: свободный | Студентов: 4378 / 711 | Оценка: 4.09 / 3.28 | Длительность: 11:25:00

Тема: Математика

Специальности: Математик

Теги: линейные пространства, метод Гауса, определители, векторы, матрицы

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Матричный метод решения систем линейных уравнений

Рассмотрим для определенности систему трех линейных уравнений с тремя неизвестными:

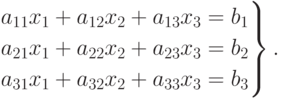$\left. \begin{aligned} a_{11}x_1+a_{12}x_2+a_{13}x_3=b_1 \\ a_{21}x_1+a_{22}x_2+a_{23}x_3=b_2 \\ a_{31}x_1+a_{32}x_2+a_{33}x_3=b_3 \end{aligned} \right\}.$

( 4.14)

Составив матрицы из коэффициентов системы, неизвестных и свободных членов, т.е.

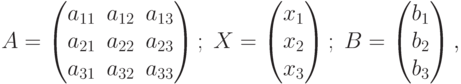
$A= \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}; \; X= \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}; \; B= \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix},$

перепишем систему (14) в матричной форме:

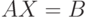( 4.15)

Искомой в этом уравнении является матрица-столбец (или вектор-столбец) Х. Пусть А – невырожденная матрица, то есть $detA \ne 0$ , и, следовательно, она имеет обратную матрицу А_-1. Умножив обе части (4.15) на А_-1 слева, получаем:

A_-1(AX)=A_-1B=>(A_-1A)X=A_-1B=>EX=A_-1B, т.е.

$X=A^{-1}B$

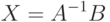( 4.16)

и есть искомое решение системы (4.14). Действительно, подставив (4.16) в (4.14), получим:

A(A_-1B)=(A_-1A)B=EB=B.

Пример 7. Решить систему матричным методом:

$\left\{ \begin{aligned} &x+2y+z=3; \\ &2x+y-z=-6; \\ &3x+y+2z=1. \end{aligned} \right.$

Решение. Запишем систему в матричной форме:

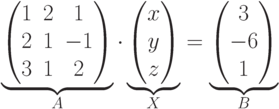
$\underbrace{ \begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & -1 \\ 3 & 1 & 2 \end{pmatrix} }_{A} \cdot \underbrace{ \begin{pmatrix} x \\ y \\ z \end{pmatrix} }_{X} = \underbrace{ \begin{pmatrix} 3 \\ -6 \\ 1 \end{pmatrix} }_{B}$

и убедимся, что данная система совместно и имеет единственное решение. Для этого найдем главный определитель системы (детерминант матрицы A ).

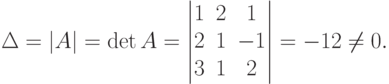
$\Delta=|A|=\det A= \begin{vmatrix} 1 & 2 & 1 \\ 2 & 1 & -1 \\ 3 & 1 & 2 \end{vmatrix} =-12 \ne 0.$

Так как детерминант матрицы A отличен от нуля, следовательно обратная матрица существует и указанный метод применим к решению системы.

Для составления присоединенной матрицы А^* найдем алгебраические дополнения

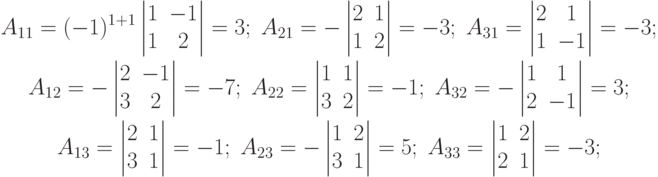
$\begin{gathered} A_{11}=(-1)^{1+1}\begin{vmatrix}1 & -1 \\ 1 & 2 \end{vmatrix}=3; \; A_{21}=-\begin{vmatrix}2 & 1 \\ 1 & 2 \end{vmatrix}=-3; \; A_{31}=\begin{vmatrix}2 & 1 \\ 1 & -1 \end{vmatrix}=-3; \\ A_{12}=-\begin{vmatrix}2 & -1 \\ 3 & 2 \end{vmatrix}=-7; \; A_{22}=\begin{vmatrix}1 & 1 \\ 3 & 2 \end{vmatrix}=-1; \; A_{32}=-\begin{vmatrix}1 & 1 \\ 2 & -1 \end{vmatrix}=3; \\ A_{13}=\begin{vmatrix}2 & 1 \\ 3 & 1 \end{vmatrix}=-1; \; A_{23}=-\begin{vmatrix}1 & 2 \\ 3 & 1 \end{vmatrix}=5; \; A_{33}=\begin{vmatrix}1 & 2 \\ 2 & 1 \end{vmatrix}=-3; \end{gathered}$

Составляем присоединенную матрицу А^*:

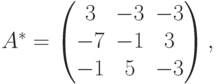
$A^*= \begin{pmatrix} 3 & -3 & -3 \\ -7 & -1 & 3 \\ -1 & 5 & -3 \end{pmatrix},$

следовательно, обратная матрица будет

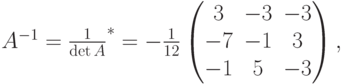
$A^{-1}=\frac{1}{\det A}\cdotA^*=-\frac{1}{12} \begin{pmatrix} 3 & -3 & -3 \\ -7 & -1 & 3 \\ -1 & 5 & -3 \end{pmatrix},$

Тогда

$X=A^{-1}B=-\frac{1}{12} \begin{pmatrix} 3 & -3 & -3 \\ -7 & -1 & 3 \\ -1 & 5 & -3 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ -6 \\ 1 \end{pmatrix} =-\frac{1}{12}\cdot \begin{pmatrix} 3\cdot 3 + (-3)\cdot(-6)+(-3)\cdot 1 \\ (-7)\cdot 3 + (-1)\cdot(-6)+3\cdot 1 \\ (-1)\cdot 3 + 5\cdot(-6)+(-3)\cdot 1 \end{pmatrix} =-\frac{1}{12}\cdot \begin{pmatrix} 24 \\ -12 \\ -36 \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}.$

Т.е. х = -2; у = 1; z = 3.

Дальше >>

Авторизоваться

Введение в линейную алгебру

Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ

Матричный метод решения систем линейных уравнений

Вопросы и ответы