|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Раскраски
Теорема 1. Для любого графа  справедливы
неравенства
справедливы
неравенства 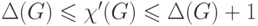 .
.
Доказательство. Приводимое ниже доказательство дает и план
алгоритма для раскрашивания ребер графа не более чем в 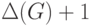 цветов. Оно основано на двух операциях перекрашивания, с описания которых
и начнем. Далее будут рассматриваться частичные реберные раскраски, т.е.
правильные раскраски, при которых некоторые ребра остаются неокрашенными.
цветов. Оно основано на двух операциях перекрашивания, с описания которых
и начнем. Далее будут рассматриваться частичные реберные раскраски, т.е.
правильные раскраски, при которых некоторые ребра остаются неокрашенными.
Допустим, ребра графа  правильно (может быть, частично)
раскрашены. Пусть
правильно (может быть, частично)
раскрашены. Пусть  и
и  - два из
использованных в
этой раскраске цветов. Рассмотрим подграф
- два из
использованных в
этой раскраске цветов. Рассмотрим подграф  , образованный всеми
ребрами, имеющими цвета
, образованный всеми
ребрами, имеющими цвета  или
или  .
В этом подграфе
степень каждой вершины не превосходит 2, следовательно, каждая компонента
связности в нем является цепью или циклом. Такую компоненту будем называть
.
В этом подграфе
степень каждой вершины не превосходит 2, следовательно, каждая компонента
связности в нем является цепью или циклом. Такую компоненту будем называть 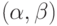 - компонентой. Если в какой-нибудь
- компонентой. Если в какой-нибудь 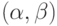 -компоненте поменять местами
цвета
-компоненте поменять местами
цвета  и
и  (т.е. все ребра, окрашенные в цвет
(т.е. все ребра, окрашенные в цвет  , перекрасить в цвет
, перекрасить в цвет  и наоборот), то полученная раскраска тоже будет
правильной.
Эту операцию назовем перекраской
и наоборот), то полученная раскраска тоже будет
правильной.
Эту операцию назовем перекраской 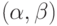 -компоненты.
-компоненты.
Другая операция применяется к частично раскрашенному подграфу,
называемому веером. Будем
говорить, что при данной
раскраске цвет  отсутствует в вершине
отсутствует в вершине  , если ни одно из ребер, инцидентных
вершине
, если ни одно из ребер, инцидентных
вершине  , не окрашено в этот цвет. Веером называется подграф
, не окрашено в этот цвет. Веером называется подграф 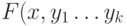 ,
, 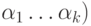 ,
состоящий из вершин
,
состоящий из вершин 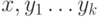 и ребер
и ребер  , в котором:
, в котором:
- ребро
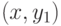 не окрашено;
не окрашено; - ребро
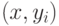 окрашено в цвет
окрашено в цвет 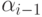 ,
, 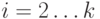 ;
; - в вершине
 отсутствует цвет
отсутствует цвет 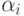 ,
, 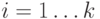 ;
; -
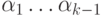 все попарно различны.
все попарно различны.
Перекраска веера состоит в том,
что ребра 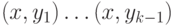 окрашиваются соответственно в цвета
окрашиваются соответственно в цвета 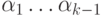 ,
а ребро
,
а ребро 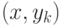 становится неокрашенным. Очевидно,
новая частичная раскраска тоже будет правильной. На рис. 10.3 слева показан
веер, а справа - результат его перекраски. Цвета ребер представлены
числами, а отсутствующие цвета в вершинах - числами со знаком минус.
Неокрашенное ребро изображено пунктиром.
становится неокрашенным. Очевидно,
новая частичная раскраска тоже будет правильной. На рис. 10.3 слева показан
веер, а справа - результат его перекраски. Цвета ребер представлены
числами, а отсутствующие цвета в вершинах - числами со знаком минус.
Неокрашенное ребро изображено пунктиром.
Покажем, что с помощью этих двух процедур перекрашивания можно ребра
любого графа  окрасить в не более чем
окрасить в не более чем 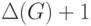 цветов.
Допустим, что уже построена частичная правильная раскраска, использующая
не более чем
цветов.
Допустим, что уже построена частичная правильная раскраска, использующая
не более чем 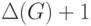 цветов, и имеется неокрашенное ребро
цветов, и имеется неокрашенное ребро  . Так как число разрешенных цветов больше, чем максимальная
степень вершины, то в каждой вершине какой-нибудь цвет отсутствует.
Допустим, в вершине
. Так как число разрешенных цветов больше, чем максимальная
степень вершины, то в каждой вершине какой-нибудь цвет отсутствует.
Допустим, в вершине  отсутствует цвет
отсутствует цвет  .
.
Будем строить веер следующим образом. Положим 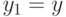 и пусть
и пусть 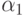 - цвет, отсутствующий в вершине
- цвет, отсутствующий в вершине  .
Получаем веер
.
Получаем веер 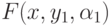 . Допустим, веер
. Допустим, веер 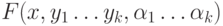 уже построен. Если
цвет
уже построен. Если
цвет 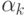 отличен от
отличен от 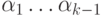 и имеется
инцидентное вершине
и имеется
инцидентное вершине  ребро
ребро 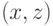 этого цвета,
то увеличиваем
этого цвета,
то увеличиваем  на 1 и полагаем
на 1 и полагаем  ,
, 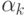 - цвет,
отсутствующий в вершине
- цвет,
отсутствующий в вершине  . Этот процесс построения веера
продолжается до тех пор, пока не наступит одно из следующих событий.
. Этот процесс построения веера
продолжается до тех пор, пока не наступит одно из следующих событий.
(А) Нет ребра цвета 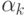 , инцидентного
вершине
, инцидентного
вершине  .
Перекрашиваем веер, в результате ребро
.
Перекрашиваем веер, в результате ребро  становится
окрашенным,
а ребро
становится
окрашенным,
а ребро 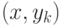 - неокрашенным, причем
цвет
- неокрашенным, причем
цвет 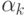 отсутствует и в вершине
отсутствует и в вершине 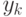 , и в вершине
, и в вершине  . Но
тогда можно
это ребро окрасить в цвет
. Но
тогда можно
это ребро окрасить в цвет 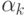 , и мы получим правильную
раскраску, в которой на одно окрашенное ребро больше.
, и мы получим правильную
раскраску, в которой на одно окрашенное ребро больше.
(Б) Цвет 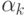 совпадает с одним из цветов
совпадает с одним из цветов 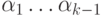 (именно этот случай изображен на рис. 10.3).
Пусть
(именно этот случай изображен на рис. 10.3).
Пусть  . Рассмотрим
вершины
. Рассмотрим
вершины 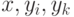 .
В каждой из них отсутствует какой-нибудь из цветов
.
В каждой из них отсутствует какой-нибудь из цветов  или
или 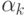 . Значит, в подграфе, образованном ребрами этих двух
цветов, степень каждой из этих вершин не превосходит 1. Следовательно, все
три вершины не могут принадлежать
одной
. Значит, в подграфе, образованном ребрами этих двух
цветов, степень каждой из этих вершин не превосходит 1. Следовательно, все
три вершины не могут принадлежать
одной 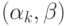 -компоненте.
Рассмотрим две возможности.
-компоненте.
Рассмотрим две возможности.
(Б1) Вершины  и
и  принадлежат разным
принадлежат разным 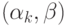 -компонентам.
Перекрасим веер
-компонентам.
Перекрасим веер 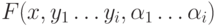 .
Ребро
.
Ребро 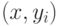 станет
неокрашенным. Теперь перекрасим
станет
неокрашенным. Теперь перекрасим 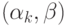 -компоненту,
содержащую вершину
-компоненту,
содержащую вершину  . После этого цвет
. После этого цвет  будет
отсутствовать в вершине
будет
отсутствовать в вершине  и ребро
и ребро 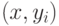 можно
окрасить в этот цвет.
можно
окрасить в этот цвет.
(Б2) Вершины  и
и 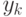 принадлежат
разным
принадлежат
разным 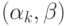 -компонентам.
Перекрасим веер
-компонентам.
Перекрасим веер 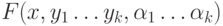 . Ребро
. Ребро 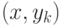 станет
неокрашенным. Теперь перекрасим
станет
неокрашенным. Теперь перекрасим 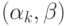 -компоненту,
содержащую вершину
-компоненту,
содержащую вершину 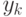 . После этого цвет
. После этого цвет  будет
отсутствовать в вершине
будет
отсутствовать в вершине 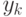 и ребро
и ребро 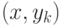 можно
окрасить в этот цвет.
можно
окрасить в этот цвет.
Итак, в любом случае получаем правильную раскраску, в которой добавилось
еще одно раскрашенное ребро  .
.
На рис. 10.4 иллюстрируются случаи (Б1) и (Б2) на примере веера из
рисунка 10.3. Здесь  ,
, 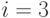 .
Левое изображение соответствует случаю (Б1):
вершины
.
Левое изображение соответствует случаю (Б1):
вершины  и
и 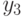 принадлежат разным
принадлежат разным  -компонентам.
После перекраски веера
-компонентам.
После перекраски веера  и
и 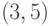 -компоненты,
содержащей вершину
-компоненты,
содержащей вершину 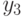 , появляется возможность
окрасить ребро
, появляется возможность
окрасить ребро 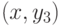 в цвет 5.
Случай (Б2) показан справа: здесь
вершины
в цвет 5.
Случай (Б2) показан справа: здесь
вершины  и
и 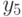 принадлежат разным
принадлежат разным  -компонентам,
поэтому после перекраски веера
-компонентам,
поэтому после перекраски веера  ,
,  ,
,  ,
,  ,
, 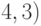 и
и 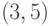 -компоненты, содержащей
вершину
-компоненты, содержащей
вершину 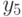 , появляется возможность окрасить
ребро
, появляется возможность окрасить
ребро 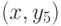 в цвет 5.
в цвет 5.
Итак, все графы делятся на два класса: у одних хроматический индекс равен
максимальной степени вершины, у других он на единицу больше. Оказывается,
определение принадлежности графа к тому или иному классу является
NP-трудной задачей. Алгоритм, который можно извлечь из доказательства
теоремы 1, за полиномиальное время находит раскраску в не более чем 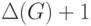 цветов. Его можно назвать "идеальным"
приближенным
алгоритмом - более высокую точность имеет только точный алгоритм.
цветов. Его можно назвать "идеальным"
приближенным
алгоритмом - более высокую точность имеет только точный алгоритм.