|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Потоки
Задача о максимальном потоке
В этой лекции будем рассматривать ориентированные графы без петель
и кратных ребер. Для вершины  множество всех входящих в нее
ребер обозначается через
множество всех входящих в нее
ребер обозначается через 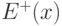 , а множество выходящих -
через
, а множество выходящих -
через 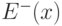 . Сетью
называется орграф, в котором:
. Сетью
называется орграф, в котором:
- каждому ребру
 приписано положительное число
приписано положительное число 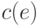 ,
называемое пропускной
способностью ребра ;
,
называемое пропускной
способностью ребра ; - выделены две вершины
 и
и  , называемые
соответственно источником и стоком,
при этом
, называемые
соответственно источником и стоком,
при этом 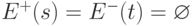 .
.
Вершины сети, отличные от источника и стока, будем называть внутренними.
Пусть задана сеть  с множеством вершин
с множеством вершин  и множеством
ребер
и множеством
ребер  . Функция
. Функция  с вещественными
значениями, определенная на
с вещественными
значениями, определенная на  , называется потоком в сети
, называется потоком в сети  ,
если она удовлетворяет следующим условиям:
,
если она удовлетворяет следующим условиям:
На рис. 16.1 показан пример сети и потока в ней. Число, вписанное в примыкающий к ребру квадрат, представляет пропускную способность, а другое число, написанное около ребра, - величину потока.
Условие (2), называемое условием сохранения потока, иногда удобно
представлять в несколько иной форме. Пусть  - любая
числовая
функция, определенная на ребрах сети. Дивергенцией функции
- любая
числовая
функция, определенная на ребрах сети. Дивергенцией функции  в вершине
в вершине  называется величина
называется величина
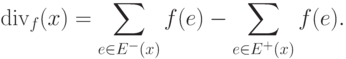
Заметим, что для любой такой функции  имеет место равенство
имеет место равенство
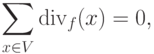 |
( 1) |
так как каждое ребро является входящим для одной вершины и выходящим для
другой, и, следовательно, каждое ребро  в этой сумме
представлено двумя слагаемыми:
в этой сумме
представлено двумя слагаемыми:  и
и 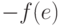 .
.
Условие сохранения означает, что дивергенция потока в каждой внутренней
вершине должна быть равна  . Поэтому из равенства (1) следует,
что для
потока
. Поэтому из равенства (1) следует,
что для
потока 
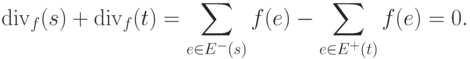
Величина
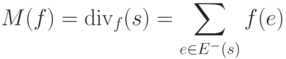
называется величиной
потока. В примере на рис. 16.1 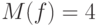 . Задача о максимальном
потоке состоит в том,
чтобы для данной сети найти поток наибольшей величины.
. Задача о максимальном
потоке состоит в том,
чтобы для данной сети найти поток наибольшей величины.

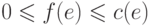 для каждого ребра
для каждого ребра 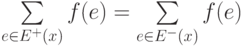 для каждой
для каждой 