|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Важнейшие классы графов
Деревья
Деревом называется связный граф, не имеющий циклов. В графе без циклов, таким образом, каждая компонента связности является деревом. Такой граф называют лесом.
Из теоремы 2
"Маршруты, связность, расстояния"
следует, что во всяком дереве, в котором не
меньше двух вершин, имеется вершина степени 1. Такие вершины называют висячими вершинами, или листьями. В действительности
легко
доказать, что в каждом дереве не меньше двух листьев, а цепь 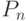 -
пример дерева, в котором точно два листа.
-
пример дерева, в котором точно два листа.
В следующих двух теоремах устанавливаются некоторые свойства деревьев.
Теорема 1. Граф с  вершинами и
вершинами и  ребрами является деревом
тогда
и только тогда, когда он
удовлетворяет любым двум из следующих трех условий:
ребрами является деревом
тогда
и только тогда, когда он
удовлетворяет любым двум из следующих трех условий:
- (1) связен;
- (2) не имеет циклов;
- (3)
 .
.
Доказательство.
Первые два условия вместе составляют определение дерева. Покажем, что выполнение любых двух из условий (1)-(3) влечет за собой выполнение третьего.
(1) и (2)  (3). Индукция по числу вершин. При
(3). Индукция по числу вершин. При 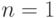 утверждение очевидно. При
утверждение очевидно. При  в дереве имеется хотя бы один
лист.
Если из дерева удалить лист, то снова получится дерево, так как циклов не
появится, а связность, очевидно, сохранится. В этом новом дереве
в дереве имеется хотя бы один
лист.
Если из дерева удалить лист, то снова получится дерево, так как циклов не
появится, а связность, очевидно, сохранится. В этом новом дереве  вершин и, по предположению индукции,
вершин и, по предположению индукции,  ребра. Следовательно,
в исходном дереве было
ребра. Следовательно,
в исходном дереве было  ребро.
ребро.
(2) и (3)  (1). Пусть в графе, не имеющем циклов,
(1). Пусть в графе, не имеющем циклов,  ребро, а его компонентами связности являются
ребро, а его компонентами связности являются 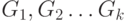 ,
причем
,
причем 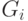 состоит из
состоит из 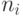 вершин,
вершин, 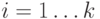 .
Каждая компонента является деревом, поэтому, как доказано выше, число
ребер в
.
Каждая компонента является деревом, поэтому, как доказано выше, число
ребер в 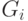 равно
равно 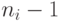 , а всего ребер в
графе
, а всего ребер в
графе 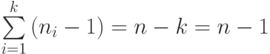 .
Значит,
.
Значит, 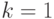 и граф связен.
и граф связен.
(1) и (3)  (2). Рассмотрим связный граф
с
(2). Рассмотрим связный граф
с  ребром.
Если бы в нем был цикл, то, удалив любое цикловое ребро, мы получили бы
связный граф с меньшим числом ребер. Можно продолжать такое удаление ребер
до тех пор, пока не останется связный граф без циклов, то есть дерево.
Но ребер в этом дереве было бы меньше, чем
ребром.
Если бы в нем был цикл, то, удалив любое цикловое ребро, мы получили бы
связный граф с меньшим числом ребер. Можно продолжать такое удаление ребер
до тех пор, пока не останется связный граф без циклов, то есть дерево.
Но ребер в этом дереве было бы меньше, чем  , а это противоречит
доказанному выше.
, а это противоречит
доказанному выше.
Теорема 2. Если  - дерево, то
- дерево, то
- в
 любая пара вершин соединена единственным
путем;
любая пара вершин соединена единственным
путем; - при добавлении к
 любого нового ребра образуется
цикл;
любого нового ребра образуется
цикл; - при удалении из
 любого ребра он превращается
в несвязный граф.
любого ребра он превращается
в несвязный граф.
Доказательство.
Существование пути между любыми двумя вершинами
следует из связности дерева. Допустим, что в некотором дереве существуют
два различных пути, соединяющих вершины  и
и  .
Начальные отрезки этих путей совпадают (оба пути начинаются в одной и той
же вершине
.
Начальные отрезки этих путей совпадают (оба пути начинаются в одной и той
же вершине  ). Пусть
). Пусть  - последняя вершина
этого совпадающего
начала, а после
- последняя вершина
этого совпадающего
начала, а после  в одном пути следует
вершина
в одном пути следует
вершина 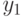 ,
а в другом - вершина
,
а в другом - вершина 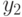 . Рассмотрим ребро
. Рассмотрим ребро 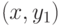 .
Если его удалить из графа, то в оставшемся подграфе вершины
.
Если его удалить из графа, то в оставшемся подграфе вершины 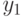 и
и  будут соединимыми - соединяющий их маршрут можно
построить так:
взять отрезок первого пути от
будут соединимыми - соединяющий их маршрут можно
построить так:
взять отрезок первого пути от 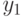 до
до  и к нему
присоединить
отрезок второго от
и к нему
присоединить
отрезок второго от  до
до  , взятый в обратном
порядке. Но это
означает, что ребро
, взятый в обратном
порядке. Но это
означает, что ребро 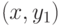 не является перешейком.
Однако из теоремы 4
"Маршруты, связность, расстояния"
следует, что в дереве каждое ребро
является перешейком. Этим доказано утверждение 1). Утверждения 2) и 3)
следуют из 1).
не является перешейком.
Однако из теоремы 4
"Маршруты, связность, расстояния"
следует, что в дереве каждое ребро
является перешейком. Этим доказано утверждение 1). Утверждения 2) и 3)
следуют из 1).
Отметим, что единственный путь, соединяющий две вершины дерева, всегда простой (если путь не является простым, в нем обязательно содержится цикл).
