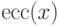|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Маршруты, связность, расстояния
Связность и компоненты
Граф называется связным, если в нем для любых двух вершин имеется маршрут, соединяющий эти вершины. Заметим, что ввиду теоремы 1 можно в этом определении заменить слово "маршрут" словами "простой путь".
Для произвольного графа определим на множестве вершин отношение
соединимости: вершина  соединима с вершиной
соединима с вершиной  ,
если существует соединяющий их маршрут.
Легко видеть, что это отношение
рефлексивно, симметрично и транзитивно, то есть является отношением
эквивалентности. Классы эквивалентности называются областями
связности, а порождаемые ими подграфы - компонентами связности
графа. В связном графе имеется только одна компонента связности -
весь граф. Компоненты связности можно определить также
как максимальные по включению связные подграфы данного графа.
,
если существует соединяющий их маршрут.
Легко видеть, что это отношение
рефлексивно, симметрично и транзитивно, то есть является отношением
эквивалентности. Классы эквивалентности называются областями
связности, а порождаемые ими подграфы - компонентами связности
графа. В связном графе имеется только одна компонента связности -
весь граф. Компоненты связности можно определить также
как максимальные по включению связные подграфы данного графа.
У графа на рис. 2.2 имеется
четыре области
связности -  ,
, 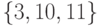 ,
, 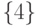 ,
, 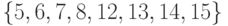 .
.
Вершина называется шарниром
(или точкой
сочленения ), если при
ее удалении число компонент связности увеличивается. У графа
на рис. 2.2 имеется четыре шарнира - это вершины  ,
, 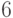 ,
, 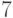 ,
,  .
.
Ребро, при удалении которого увеличивается число компонент связности,
называется перешейком.
Перешейками графа, изображенного
на рис. 2.2, являются ребра 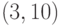 ,
, 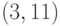 ,
, 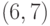 ,
,  ,
, 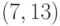 .
.
Легко доказываются следующие свойства шарниров и перешейков:
Теорема 3.Вершина  является шарниром тогда и только тогда,
когда в графе имеются такие отличные от
является шарниром тогда и только тогда,
когда в графе имеются такие отличные от  вершины
вершины  и
и  , что любой путь,
соединяющий
, что любой путь,
соединяющий  и
и  , проходит через
, проходит через  .
.
Теорема 4. Ребро является перешейком в том и только том случае, если в графе нет простого цикла, содержащего это ребро.
Метрические характеристики графов
Расстоянием между двумя
вершинами графа называется наименьшая длина
пути, соединяющего эти вершины. Расстояние между вершинами  и
и  обозначается через
обозначается через 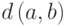 . Если в
графе нет пути,
соединяющего
. Если в
графе нет пути,
соединяющего  и
и  , то есть эти вершины принадлежат
разным
компонентам связности, то расстояние между ними считается бесконечным.
, то есть эти вершины принадлежат
разным
компонентам связности, то расстояние между ними считается бесконечным.
Функция  обладает следующими свойствами:
обладает следующими свойствами:
-
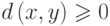 , причем
, причем 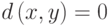 тогда
и только тогда, когда
тогда
и только тогда, когда 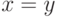 ;
; -
 ;
; -
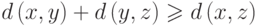 (неравенство треугольника).
(неравенство треугольника).
В математике функцию двух переменных, определенную на некотором множестве и удовлетворяющую условиям 1 - 3, называют метрикой, а множество, на котором задана метрика, - метрическим пространством. Таким образом, множество вершин любого графа можно рассматривать как метрическое пространство.
Расстояние от данной вершины  до наиболее удаленной от нее
вершины
называется эксцентриситетом вершины
до наиболее удаленной от нее
вершины
называется эксцентриситетом вершины  и обозначается
через
и обозначается
через 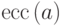 . Таким образом,
. Таким образом,

Вершину с наименьшим эксцентриситетом называют центральной,
а вершину с наибольшим эксцентриситетом - периферийной.
Множество всех центральных вершин называется центром графа.
Сама величина наименьшего эксцентриситета
называется радиусом графа и
обозначается
через 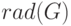 , а величина наибольшего - диаметром
и обозначается
, а величина наибольшего - диаметром
и обозначается  . Иначе говоря,
. Иначе говоря,
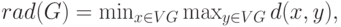

Наименьший диаметр имеет полный граф - его диаметр равен 1. Среди
связных
графов с  вершинами наибольший диаметр, равный
вершинами наибольший диаметр, равный  ,
имеет
цепь
,
имеет
цепь 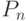 .
.
Если расстояние между двумя вершинами равно диаметру графа, то кратчайший путь, соединяющий эти вершины, называется диаметральным путем, а подграф, образованный вершинами и ребрами этого пути, - диаметральной цепью.
Для графа, изображенного на рис. 2.3, эксцентриситеты вершин приведены в следующей таблице:
Центр этого графа составляют вершины  ,
, 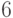 ,
, 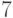 ;
периферийные вершины -
;
периферийные вершины -  ,
, 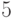 и
и 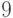 ;
радиус его
равен
;
радиус его
равен  , а диаметр
, а диаметр 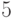 . Одна из диаметральных цепей
порождается множеством вершин
. Одна из диаметральных цепей
порождается множеством вершин 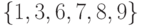 .
.