|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Списки
Деревья и графы
Деревья находят широкое применение при проектировании алгоритмов и,
в частности, структур данных. Отсылая читателя к литературе по теории
графов, мы будем пользоваться такими понятиями, как узел, ребро, лист,
потомок, сын, левый потомок, правый потомок, предок, отец, корень, ветвь
и другие. Регулярным деревом назовем дерево, в котором фиксировано
максимально возможное (как правило, небольшое) число потомков для каждого
из его узлов. В частности, если число потомков для каждого узла не больше
двух, то дерево называется бинарным, если не более трех — тернарным. Если
это число может равняться только двум или трем, то дерево называется
(  —
—  )-деревом.
)-деревом.
Достаточно универсальным является способ представления регулярных деревьев, при котором каждый узел представляется записью, содержащей, кроме прикладной информации, позиции смежных с ним элементов, например позиции потомков или наряду с потомками позицию предка или еще каких-либо узлов, в зависимости от потребностей. Регулярность дерева позволяет фиксировать число полей, достаточное для представления любого узла.
Так, узлы бинарного корневого дерева можно представлять записями вида
![\eq*{
[{\rm Element}, {\rm Left}, {\rm Right}],
}](/sites/default/files/tex_cache/83f2c74d7ac502fe7469e950e8c8958f.png)
 представляет связанную с узлом прикладную
информацию,
представляет связанную с узлом прикладную
информацию, 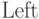 — позицию его левого потомка,
а
— позицию его левого потомка,
а  — позицию правого потомка. Само дерево
в таком случае можно представить позицией его корня. Если в алгоритме
необходимо продвижение от узла к предку, то узлы бинарного корневого
дерева можно представлять записями вида
— позицию правого потомка. Само дерево
в таком случае можно представить позицией его корня. Если в алгоритме
необходимо продвижение от узла к предку, то узлы бинарного корневого
дерева можно представлять записями вида![\eq*{
[{\rm Element}, {\rm Left}, {\rm Right}, {\rm Father}],
}](/sites/default/files/tex_cache/ee684efa6f60637a2b27c89a650b1862.png)
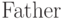 — позиция предка рассматриваемого узла.
— позиция предка рассматриваемого узла.Для представления нерегулярных деревьев (то есть деревьев, узлы которых могут иметь произвольное число потомков) применяют следующий способ: потомки каждого узла нумеруются и каждый узел представляется записью, включающей в себя позицию его первого (левого) потомка и позицию его "правого брата".
Для регулярных деревьев более экономным по памяти может оказаться
представление с помощью массива. Рассмотрим этот прием на примере
бинарного дерева. Значения индексов массива отождествляются с узлами
дерева, пронумерованными так, что корень получает номер 1, а потомки узла
c номером  получают номера
получают номера 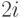 и
и 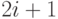 . При таком
представлении предок узла с номером
. При таком
представлении предок узла с номером  будет иметь номер
будет иметь номер  (частное от деления
(частное от деления  на 2). Аналогично можно представить
тернарное и другие регулярные деревья.
на 2). Аналогично можно представить
тернарное и другие регулярные деревья.
Остановимся вкратце на представлении графов общего вида. Обыкновенный граф
с  вершинами часто представляют матрицей смежности, то есть
матрицей размером
вершинами часто представляют матрицей смежности, то есть
матрицей размером  , в которой элемент, расположенный
в
, в которой элемент, расположенный
в  -й строке и
-й строке и  -м столбце, равен
-м столбце, равен  ,
если вершины графа
с номерами
,
если вершины графа
с номерами  ,
,  соединены ребром, и равен 0, если
такого ребра нет. Если граф не ориентирован, то его матрица смежности симметрична
и можно ограничиться хранением ее треугольной части.
соединены ребром, и равен 0, если
такого ребра нет. Если граф не ориентирован, то его матрица смежности симметрична
и можно ограничиться хранением ее треугольной части.
Матричный способ представления может оказаться неэкономным с точки зрения
использования памяти, если граф разрежен. Так, например, известно, что
число ребер связного планарного графа с  вершинами не превосходит
величины (
вершинами не превосходит
величины (  ) при
) при  , то есть оценивается
величиной
, то есть оценивается
величиной  ,
а не как в общем случае
,
а не как в общем случае 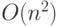 . Представлять
такие графы матрицей смежности, как правило, нецелесообразно.
. Представлять
такие графы матрицей смежности, как правило, нецелесообразно.
Другой способ представления графа — это список или массив пар вершин,
соответствующих ребрам. При таком способе, если граф не ориентирован, то
из двух возможных пар (  ,
,  ) и (
) и (  ,
,  )
целесообразно хранить только одну, например ту, у которой первая
компонента меньше второй.
)
целесообразно хранить только одну, например ту, у которой первая
компонента меньше второй.
Еще один способ, часто имеющий преимущества перед названными выше, — это представление графа массивом или списком списков (рис. 2.7).
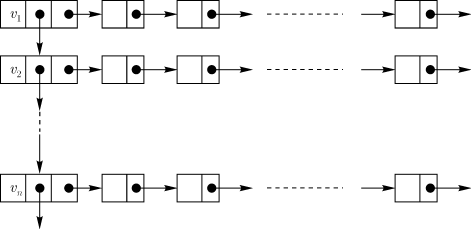
Рис. 2.7. Представление графа комбинацией списков: множество вершин представлено списком узлов, к каждому из которых справа подцеплен список смежных с ним вершин
А именно, для каждой вершины организуется список смежных с ней вершин.
В этом случае легко осуществляется доступ к окрестностям вершин. Примерно
такого же эффекта можно достичь, представляя граф с помощью двух массивов: ![{\rm inf} [1 \ldots m]](/sites/default/files/tex_cache/594a1cbc01ce1662563a381f73552e27.png) и
и ![{\rm adr} [1\ldots n + 1)]](/sites/default/files/tex_cache/db5731eb8194a32d3926b7b77ed371df.png) ,
где
,
где  — число ребер
графа. Массив
— число ребер
графа. Массив  назовем адресным, а
назовем адресным, а  — информационным.
В информационном массиве вначале перечисляются номера вершин, смежных
с первой вершиной, затем — со второй и так далее. В адресном массиве
указываются номера позиций информационного массива так, чтобы для каждой
вершины
— информационным.
В информационном массиве вначале перечисляются номера вершин, смежных
с первой вершиной, затем — со второй и так далее. В адресном массиве
указываются номера позиций информационного массива так, чтобы для каждой
вершины  по ним можно было находить фрагменты массива
по ним можно было находить фрагменты массива  , в которых записаны номера вершин, смежных с этой вершиной. Например,
, в которых записаны номера вершин, смежных с этой вершиной. Например, ![{\rm adr}[i]](/sites/default/files/tex_cache/c6bd95d95cf340a812a1fd0d8bb102d7.png) может хранить позицию, с которой начинаются
в массиве
может хранить позицию, с которой начинаются
в массиве  вершины, смежные с
вершины, смежные с  -й, при этом
-й, при этом ![{\rm adr}[n + 1]](/sites/default/files/tex_cache/3f69bc649c3058b3db22c468c9f5d44b.png) — первая позиция
за пределами массива
— первая позиция
за пределами массива  . В таком случае, если нам
требуется с каждой
вершиной
. В таком случае, если нам
требуется с каждой
вершиной  из окрестности вершины
из окрестности вершины  выполнить
оператор
выполнить
оператор 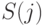 ,
то можно сделать это с помощью оператора цикла:
,
то можно сделать это с помощью оператора цикла:
![\eq*{
for k := {\rm adr}[i]\ to\ {\rm adr} [i + 1] - 1\ \t{do}
S({\rm inf}[k]).
}](/sites/default/files/tex_cache/faee56a83287906942d4b5e2f89a0940.png)
Заметим, что если граф не ориентирован, то каждое ребро (  ,
,  ) будет представлено дважды: один раз в последовательности вершин, смежных
с вершиной
) будет представлено дважды: один раз в последовательности вершин, смежных
с вершиной  , а второй раз — в последовательности вершин,
смежных с вершиной
, а второй раз — в последовательности вершин,
смежных с вершиной  . Но эта избыточность часто бывает полезна с точки
зрения времени выполнения операций над окрестностями вершин графа. Как недостаток
такого представления графа, можно отметить неудобство при динамической
модификации графа, например, добавление к графу ребра может потребовать
большого количества пересылок в массиве
. Но эта избыточность часто бывает полезна с точки
зрения времени выполнения операций над окрестностями вершин графа. Как недостаток
такого представления графа, можно отметить неудобство при динамической
модификации графа, например, добавление к графу ребра может потребовать
большого количества пересылок в массиве  . Этого недостатка лишен
способ представления графа, показанный на рис. 2.7.
. Этого недостатка лишен
способ представления графа, показанный на рис. 2.7.
