| Россия, Магнитогорск |
О решении операторных уравнений
Цель лекции: Показать способы решения операторных уравнений а гильбертовом пространстве. Реализовать с помощью объектно-ориентированного программирования на C# классы для решения этих задач.
Как мы уже отмечали, многие математические задачи могут быть записаны в виде операторных уравнений. И одной из основных задач при рассмотрении операторных уравнений является нахождение обратного оператора. Мы рассмотрим методы решения операторных уравнений, основанные на методе Галеркина. Основным модельным примером в нашем рассмотрении будет краевая (двухточечная) задача для обыкновенного дифференциального уравнения второго порядка.
Мы будем рассматривать следующее уравнение
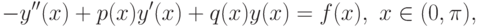 |
( 11.1) |
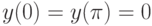 |
( 11.2) |
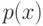 и
и 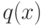 , а также функция
, а также функция  считаются
известными. Однако в этой лекции мы будем рассматривать лишь
случай, когда
считаются
известными. Однако в этой лекции мы будем рассматривать лишь
случай, когда 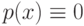 , а
, а  .
.Используя результаты предыдущей лекции, мы будем рассматривать
следующее гильбертово пространство  , в котором в
качестве базисных функций выбраны функции
, в котором в
качестве базисных функций выбраны функции
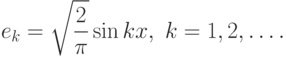
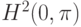 . Мы
будем говорить, что функция
. Мы
будем говорить, что функция 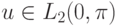 принадлежит
пространству
принадлежит
пространству 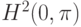 , если коэффициенты Фурье этой функции:
, если коэффициенты Фурье этой функции:
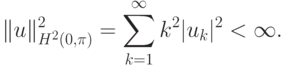
 , то вторая производная
этой функции (точнее, действие оператора
, то вторая производная
этой функции (точнее, действие оператора  ) принадлежит
) принадлежит  . Введем еще один простой оператор
. Введем еще один простой оператор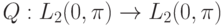
 . Очевидно, что это тоже диагональный
оператор, для которого коэффициенты
. Очевидно, что это тоже диагональный
оператор, для которого коэффициенты  равны
равны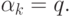
![-D^2[y]+Q[y]=f,](/sites/default/files/tex_cache/98cb1c50916c0bdeb6d36f10ca54b2e9.png) |
( 11.3) |
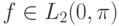 . Соответственно, решением задачи 11.3
называется функция
. Соответственно, решением задачи 11.3
называется функция  , удовлетворяющая уравнению
11.3.
, удовлетворяющая уравнению
11.3.Операторный подход позволяет довольно просто получить решение
задачи 11.3. Чтобы вывести аналитико-численные формулы,
для решения задачи 11.3 представим функцию  разложением
в ряд:
разложением
в ряд:
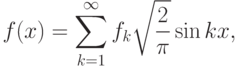
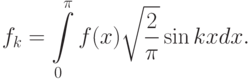
 мы будем искать в виде:
мы будем искать в виде: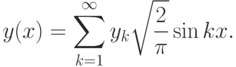
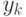 . Находить
эти числа мы будем следующим образом - подставим разложение по
базисным функциям в уравнение 11.3:
. Находить
эти числа мы будем следующим образом - подставим разложение по
базисным функциям в уравнение 11.3:![-{\cal D}^2[\sum\limits_{k=1}^\infty y_k\sqrt{\frac{2}{\pi}}\sin
kx]+Q[\sum\limits_{k=1}^\infty y_k\sqrt{\frac{2}{\pi}}\sin
kx]=\sum\limits_{k=1}^\infty f_k\sqrt{\frac{2}{\pi}}\sin kx,](/sites/default/files/tex_cache/53cc5c43b6b5ee8f064667a9aeb96a14.png)
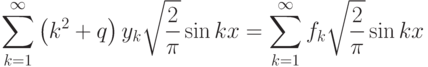
 , получаем цепочку (бесконечную)
равенств:
, получаем цепочку (бесконечную)
равенств:
 ):
):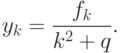
Единственный нетривиальный момент при применении нашего операторного подхода состоит в том, чтобы получить разложение правой части по выбранному базису. Однако поскольку для получения этого разложения нужно вычислять скалярные произведения, то мы можем воспользоваться ранее созданными классами для гильбертовых пространств.
