Интеллектуальные задачи в экономике
11.1. Экономика в Искусственном Интеллекте
Экономика как наука возникла в 1776 году, когда шотландский философ Адам Смит (1723—1790) опубликовал свою книгу An Inquiry into the Nature and Causes of the Wealth of Nations (Исследование о природе и причинах богатства народов). Важный вклад в экономику был сделан еще древнегреческими учёными и другими предшественниками Смита, но только Смит впервые сумел оформить эту область знаний как науку, используя идею, что любую экономику можно рассматривать как состоящую из отдельных агентов, стремящихся максимизировать свое собственное экономическое благосостояние.
Большинство людей считают, что экономика посвящена изучению денежного оборота, но любой экономист ответит на это, что в действительности он изучает то, как люди делают выбор, который ведёт к предпочтительным для них результатам. Математическая трактовка понятия "предпочтительных результатов", или полезности, была впервые формализована Леоном Валрасом (1834—1910), уточнена Фрэнком Рамсеем, а затем усовершенствована Джоном фон Нейманом и Оскаром Моргенштерном в книге The Theory of Games and Economic Behavior (Теория игр и экономического поведения).
Теория решений, которая объединяет в себе теорию вероятностей и теорию полезности, предоставляет формальную и полную инфраструктуру для принятия решений (в области экономики или в другой области) в условиях неопределённости. Следовательно, в тех случаях, когда среда, в которой действует лицо, принимающее решение, наиболее адекватно может быть представлена лишь с помощью вероятностных описаний.
Она хорошо подходит для "крупных" экономических образований, где каждый агент не обязан учитывать действия других агентов как индивидуумов. А в "небольших" экономических образованиях ситуация в большей степени напоминает игру, поскольку действия одного игрока могут существенно повлиять на полезность действий другого (или положительно, или отрицательно).
Теория игр, разработанная фон Нейманом и Морген Штерном, позволяет сделать неожиданный вывод, что в некоторых играх рациональный агент должен действовать случайным образом или, по крайней мере, таким образом, который кажется случайным для соперников.
Экономисты чаще всего не пытаются выработать способ принятия рациональных решений в тех условиях, когда вознаграждение в ответ на определённые действия не предоставляется немедленно, а становится результатом нескольких действий, выполненных в определенной последовательности.
Изучению этой темы посвящена область исследования операций, которая возникла во время Второй мировой войны в результате усилий, которые были предприняты в Британии по оптимизации работы радарных установок, а в дальнейшем нашла применение и в гражданском обществе при выработке сложных управленческих решений.
В работе Ричарда Беллмана формализован определённый класс последовательных задач выработки решений, называемых марковскими процессами принятия решений (Markov Decision Process — MDP).
Работы в области экономики и исследования операций оказали большое влияние на сформулированное понятие рациональных агентов, но в течение многих лет исследования в области искусственного интеллекта проводились совсем по другим направлениям. Одной из причин этого была кажущаяся сложность задачи выработки рациональных решений. Тем не менее, Герберт Саймон (1916—2001) в некоторых из своих ранних работ показал, что лучшее описание фактического поведения человека дают модели, основанные на удовлетворении (принятии решений, которые являются "достаточно приемлемыми"), а не модели, предусматривающие трудоёмкий расчёт оптимального решения. Он стал одним из первых исследователей в области искусственного интеллекта, получившим Нобелевскую премию по экономике (это произошло в 1978 году). В 1990-х годах наблюдалось возрождение интереса к использованию методов теории решений для систем агентов.
11.2. Нечёткая логика
Математическая теория нечётких множеств (fuzzy sets) и нечёткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским учёным Лотфи Заде (Lotfi Zadeh) в 1965 г. Основной причиной появления новой теории стало наличие нечётких и приближённых рассуждений при описании человеком процессов, систем, объектов.
Прежде чем нечёткий подход к моделированию сложных систем получил признание во всём мире, прошло не одно десятилетие с момента зарождения теория нечётких множеств. И на этом пути развития нечётких систем принято выделять три периода.
Первый период (конец 60-х–начало 70 г.г.) характеризуется развитием теоретического аппарата нечётких множеств (Л. Заде, Э. Мамдани, Беллман). Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечёткого управления сложными техническими системами (парогенератор с нечётким управлением). Одновременно стало уделяться внимание вопросам построения экспертных систем, построенных на нечёткой логике, разработке нечётких контроллеров. Нечёткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике. Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечётких экспертных систем, а области применения нечёткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.
Триумфальное шествие нечёткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy Approximation Theorem). В бизнесе и финансах нечёткая логика получила признание после того как в 1988 году экспертная система на основе нечётких правил для прогнозирования финансовых индикаторов единственная предсказала биржевой крах. И количество успешных фаззи - применений в настоящее время исчисляется тысячами.
Математический аппарат
Характеристикой нечёткого множества выступает функция принадлежности (Membership Function). Обозначим через MFc(x) – степень принадлежности к нечёткому множеству C, представляющей собой обобщение понятия характеристической функции обычного множества. Тогда нечётким множеством С называется множество упорядоченных пар вида ![C={MF_c(x)/x}, MF_c(x) [0,1]](/sites/default/files/tex_cache/ae28f7f7625e335f028e515e436b2bc1.png) . Значение
. Значение 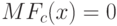 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.
означает отсутствие принадлежности к множеству, 1 – полную принадлежность.
Проиллюстрируем это на простом примере. Формализуем неточное определение "горячий чай". В качестве x (область рассуждений) будет выступать шкала температуры в градусах Цельсия. Очевидно, что она будет изменяться от 0 до 100 градусов. Нечёткое множество для понятия "горячий чай" может выглядеть следующим образом:

Так, чай с температурой 60 С принадлежит к множеству "Горячий" со степенью принадлежности 0,80. Для одного человека чай при температуре 60 С может оказаться горячим, для другого – не слишком горячим. Именно в этом и проявляется нечёткость задания соответствующего множества.
Для нечётких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчётов, являются пересечение и объединение.
Пересечение двух нечётких множеств (нечёткое "И"): A B:
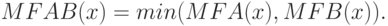
Объединение двух нечётких множеств (нечеткое "ИЛИ"):
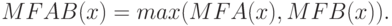
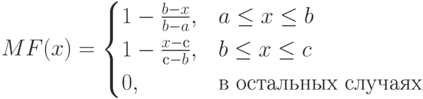
При  имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки
имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки 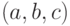 .
.
Аналогично для задания трапецеидальной функции принадлежности необходима четвёрка чисел 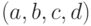 :
:

При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
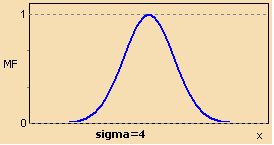
Функция принадлежности гауссова типа описывается формулой ![MF(x)=exp \left [- \left ( \frac{x-c}{\sigma}\right)^2\right]](/sites/default/files/tex_cache/61d6d94f620d845f6c07939ee410d046.png) и оперирует двумя параметрами. Параметр c обозначает центр нечёткого множества, а параметр отвечает за крутизну функции.
и оперирует двумя параметрами. Параметр c обозначает центр нечёткого множества, а параметр отвечает за крутизну функции.
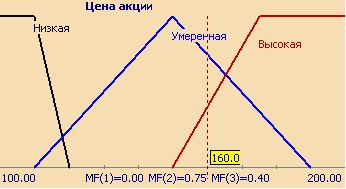
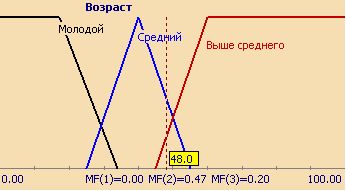
Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображается вместе на одном графике. На рис.11.3 приведён пример описанной выше лингвистической переменной "Цена акции", на рис.11.4 – формализация неточного понятия "Возраст человека". Так, для человека 48 лет степень принадлежности к множеству "Молодой" равна 0, "Средний" – 0,47, "Выше среднего" – 0,20.
Количество термов в лингвистической переменной редко превышает 7.
Нечёткий логический вывод
Основой для проведения операции нечёткого логического вывода является база правил, содержащая нечёткие высказывания в форме "Если - то" и функции принадлежности для соответствующих лингвистических термов. При этом должны соблюдаться следующие условия:
- Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.
- Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).
В противном случае имеет место неполная база нечётких правил.
Пусть в базе правил имеется m правил вида:
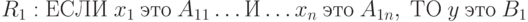
. . .
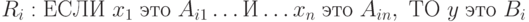
. . .
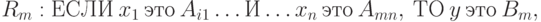
где  – входные переменные; y – выходная переменная;
– входные переменные; y – выходная переменная;  – заданные нечёткие множества с функциями принадлежности.
– заданные нечёткие множества с функциями принадлежности.
Результатом нечёткого вывода является чёткое значение переменной y* на основе заданных чётких значений  .
.
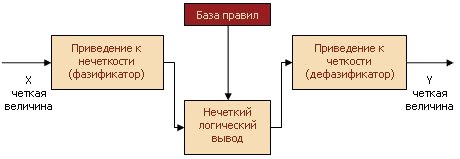
В общем случае механизм логического вывода включает четыре этапа: введение нечёткости (фазификация), нечёткий вывод, композиция и приведение к чёткости, или дефазификация (рис.11.5).
Алгоритмы нечёткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечёткого вывода Мамдани, Сугено, Ларсена, Цукамото.
Рассмотрим подробнее нечёткий вывод на примере механизма Мамдани (Mamdani). Это наиболее распространённый способ логического вывода в нечётких системах. В нём используется минимаксная композиция нечётких множеств. Данный механизм включает в себя следующую последовательность действий.
- Процедура фазификации: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как
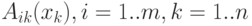 .
. - Нечёткий вывод. Сначала определяются уровни "отсечения" для левой части каждого из правил:

Далее находятся "усечённые" функции принадлежности:
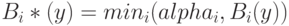
- Композиция, или объединение полученных усечённых функций, для чего используется максимальная композиция нечётких множеств:
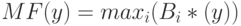 , где MF(y) – функция принадлежности итогового нечёткого множества.
, где MF(y) – функция принадлежности итогового нечёткого множества. - Дефазификация, или приведение к чёткости. Существует несколько методов дефазификации. Например, метод среднего центра, или центроидный метод:
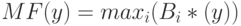
Геометрический смысл такого значения – центр тяжести для кривой MF(y). Рис.11.6 графически показывает процесс нечёткого вывода по Мамдани для двух входных переменных и двух нечётких правил R1 и R2.
Интеграция с интеллектуальными парадигмами
Гибридизация методов интеллектуальной обработки информации – девиз, под которым прошли 90-е годы у западных и американских исследователей. В результате объединения нескольких технологий искусственного интеллекта появился специальный термин – "мягкие вычисления" (soft computing), который ввел Л. Заде в 1994 году. В настоящее время мягкие вычисления объединяют такие области как: нечёткая логика, искусственные нейронные сети, вероятностные рассуждения и эволюционные алгоритмы. Они дополняют друг друга и используются в различных комбинациях для создания гибридных интеллектуальных систем.
Влияние нечёткой логики оказалось, пожалуй, самым обширным. Подобно тому, как нечёткие множества расширили рамки классической математическую теорию множеств, нечёткая логика "вторглась" практически в большинство методов Data Mining, наделив их новой функциональностью. Ниже приводятся наиболее интересные примеры таких объединений.