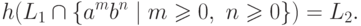|
Упражнение 2.1.25 |
Дополнительные свойства контекстно-свободных языков
11.3. Представления контекстно-свободных языков посредством гомоморфизмов
Теорема 11.3.1. Рассмотрим алфавит 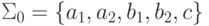 и язык
и язык 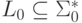 , порождаемый контекстно-свободной грамматикой G0:
, порождаемый контекстно-свободной грамматикой G0:

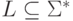 является контекстно-свободным
тогда и только тогда, когда
существует такой гомоморфизм
является контекстно-свободным
тогда и только тогда, когда
существует такой гомоморфизм 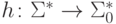 , что L = h-1(L0) или
, что L = h-1(L0) или 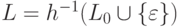 .
.Доказательство. Достаточность следует из теоремы 11.2.4. Приведем теперь идею доказательства необходимости (полное доказательство можно найти в [Сал, с. 103-109]).
Пусть дан произвольный
контекстно-свободный язык L.
Согласно теореме 8.4.6
язык 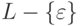 порождается некоторой
контекстно-свободной грамматикой
порождается некоторой
контекстно-свободной грамматикой 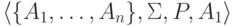 ,
в которой каждое правило имеет один из следующих трех видов:
,
в которой каждое правило имеет один из следующих трех видов:  ,
,  ,
, 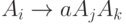 ,
где
,
где 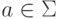 .
.
Определим вспомогательную функцию 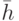 ,
ставящую в соответствие каждому символу из
,
ставящую в соответствие каждому символу из  конечный язык над алфавитом
конечный язык над алфавитом 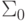 следующим образом:
следующим образом:

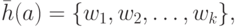

Пример 11.3.2.
Пусть 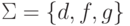 .
Рассмотрим язык L,
порождаемый грамматикой
.
Рассмотрим язык L,
порождаемый грамматикой
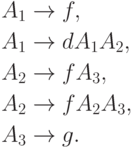
h(d) = cb1b2b1a1a2a2a1a1a2a1c, h(f) = cb1b2b1cb1b2b2b1a1a2a2a2a1cb1b2b2b1a1a2a2a2a1a1a2a2a1c, h(g) = cb1b2b2b2b1c.
Рассмотрим, например, слово 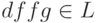 .
Проверим, что слово h(dffg)
выводится в грамматике G0
из теоремы 11.3.1.
Очевидно, что
.
Проверим, что слово h(dffg)
выводится в грамматике G0
из теоремы 11.3.1.
Очевидно, что 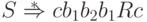 .
С помощью последних пяти правил грамматики G0
можно вывести, что
.
С помощью последних пяти правил грамматики G0
можно вывести, что

 ,
что
,
что
w1 = c, w2 = c, w3 = cb1b2b2b1a1a2a2a2a1cb1b2b2b1a1a2a2a2a1a1a2a2a1c, w4 = cb1b2b1c, w5 = cb1b2b2b1a1a2a2a2a1a1a2a2a1c, w6 = c.
Теорема 11.3.3 (Теорема Хомского-Шютценберже). Язык 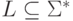 является контекстно-свободным
тогда и только тогда, когда
существуют такие
натуральное число n, автоматный язык L1 над алфавитом
является контекстно-свободным
тогда и только тогда, когда
существуют такие
натуральное число n, автоматный язык L1 над алфавитом 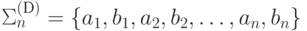 и гомоморфизм
и гомоморфизм 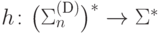 , что
, что  , где
, где 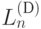 - язык Дика над 2n буквами.
- язык Дика над 2n буквами.
Доказательство можно найти в [Лал, с. 331-333].
Упражнение 11.3.4. Рассмотрим язык L1, порождаемый грамматикой
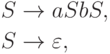
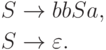
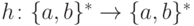 ,
что
,
что