|
Упражнение 2.1.25 |
Автоматы с магазинной памятью
10.2. Характеризация контекстно-свободных языков
Теорема 10.2.1. Если язык L является контекстно-свободным, то существует МП-автомат, распознающий этот язык.
Доказательство.
Пусть язык L порождается контекстно-свободной грамматикой  ,
в которой каждое правило имеет вид
,
в которой каждое правило имеет вид 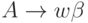 ,
где
,
где 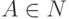 ,
, 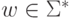 и
и 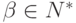 (в силу теоремы 8.8.3 такая
грамматика существует).
Положим
(в силу теоремы 8.8.3 такая
грамматика существует).
Положим 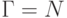 ,
, 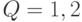 ,
, 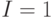 ,
,  и
и
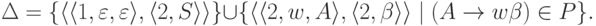
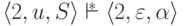 тогда и только тогда, когда
существует левосторонний вывод
тогда и только тогда, когда
существует левосторонний вывод ![\smash[b]{ S \overstar{\lmarrow} u \alpha }](/sites/default/files/tex_cache/fc0eb180441eb609e2033f0f623336a0.png) (здесь
(здесь  и
и 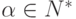 ).
).Пример 10.2.2.
Пусть  .
Контекстно-свободная грамматика
.
Контекстно-свободная грамматика
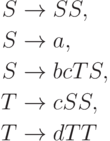
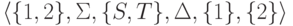 ,
где
,
где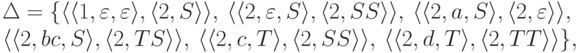
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "1,3" ^{\varepsilon,\varepsilon:S}
&
& *=[o][F=]{2}
\rloop{-1,1} ^*!/r4mm/{\varepsilon,S:SS}
\rloop{3,7} ^{a,S:\varepsilon}
\rloop{1,0} ^{bc,S:TS}
\rloop{3,-7} ^{c,T:SS}
\rloop{-1,-1} ^*!/r4mm/{d,T:TT}
}](/sites/default/files/tex_cache/52d6e6c7eac19bcb64b61fc99e76cc23.png)
Лемма 10.2.3. Каждый МП-автомат эквивалентен некоторому МП-автомату 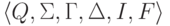 , где |I| = 1, |F| = 1 и каждый переход
, где |I| = 1, |F| = 1 и каждый переход 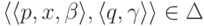 удовлетворяет требованиям
удовлетворяет требованиям  и
и 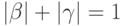 .
.
Пример 10.2.4.
Рассмотрим МП-автомат 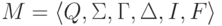 ,
где
,
где 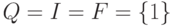 ,
, 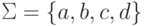 ,
, 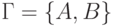 ,
,
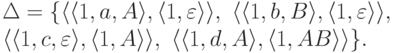
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{-1,-1} ^*!/r3mm/{a,A:\varepsilon}
\rloop{-1,1} ^*!/r3mm/{b,B:\varepsilon}
\rloop{1,1} ^*!/l3mm/{c,\varepsilon:A}
\rloop{1,-1} ^*!/l3mm/{d,A:AB}
}](/sites/default/files/tex_cache/58016d071488f0a11b4799f28fdfc555.png)
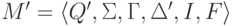 ,
где
,
где 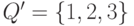 и
и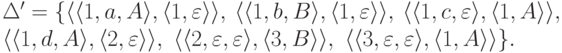
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{-1,-1} ^*!/r3mm/{a,A:\varepsilon}
\rloop{-1,1} ^*!/r3mm/{b,B:\varepsilon}
\rloop{1,1} ^*!/l3mm/{c,\varepsilon:A}
\ar "1,3" ^{d,A:\varepsilon}
&
& *=[o][F-]{2}
\ar "2,2" ^{\varepsilon,\varepsilon:B}
\\
%
& *=[o][F-]{3}
\ar "1,1" ^{\varepsilon,\varepsilon:A}
&
}](/sites/default/files/tex_cache/2d6b31cc750258c90e6fd0071fa094ee.png)
Пример 10.2.5.
Рассмотрим МП-автомат 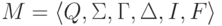 ,
где
,
где 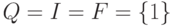 ,
, 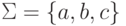 ,
, 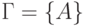 ,
,
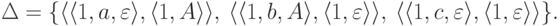
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a,\varepsilon:A}
\rloop{1,0} ^{b,A:\varepsilon}
\rloop{0,-1} ^{c,\varepsilon:\varepsilon}
}](/sites/default/files/tex_cache/89f7d36ba2c520914db061beac6986f2.png)
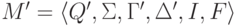 ,
где
,
где  ,
, 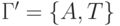 и
и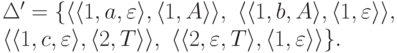
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a,\varepsilon:A}
\rloop{1,0} ^{b,A:\varepsilon}
\ar "2,1" <0.6mm> ^{c,\varepsilon:T}
\\
*=[o][F-]{2}
\ar "1,1" <0.6mm> ^{\varepsilon,T:\varepsilon}
}](/sites/default/files/tex_cache/2b445d44e5ec176afac2c167f184ede6.png)
Пример 10.2.6.
Рассмотрим МП-автомат 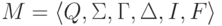 ,
где
,
где 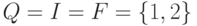 ,
, 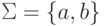 ,
, 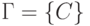 ,
,
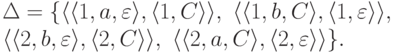
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a,\varepsilon:C}
\rloop{0,-1} ^{b,C:\varepsilon}
&
\\
%
& *=[o][F=]{2}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a,\varepsilon:C}
\rloop{0,-1} ^{a,C:\varepsilon}
}](/sites/default/files/tex_cache/d29c0662434b21d05a69dc1329b02599.png)
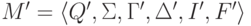 ,
где
,
где 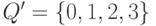 ,
, 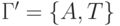 ,
,  ,
, 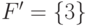 ,
,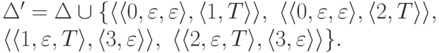
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
%
& *=[o][F-]{1}
\rloop{0,1} ^{a,\varepsilon:C}
\rloop{0,-1} ^{b,C:\varepsilon}
\ar "1,4" ^{\varepsilon,T:\varepsilon}
&
& *=[o][F=]{3}
\\
*=[o][F-]{0}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" ^{\varepsilon,\varepsilon:T}
\ar "2,3" _{\varepsilon,\varepsilon:T}
&
& *=[o][F-]{2}
\rloop{0,1} ^{a,\varepsilon:C}
\rloop{0,-1} ^{a,C:\varepsilon}
\ar "1,4" _{\varepsilon,T:\varepsilon}
&
}](/sites/default/files/tex_cache/ed7b0b1c91bc4470493d6bb048000137.png)
Теорема 10.2.7. Если язык L распознается некоторым МП-автоматом, то L является контекстно-свободным.
Доказательство.
Пусть язык L распознается МП-автоматом 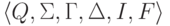 .
Без ограничения общности можно считать,
что
.
Без ограничения общности можно считать,
что 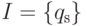 ,
, 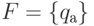 и каждый переход
и каждый переход 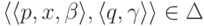 удовлетворяет требованию
удовлетворяет требованию 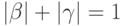 .
Построим искомую
контекстно-свободную грамматику
.
Построим искомую
контекстно-свободную грамматику  ,
положив
,
положив 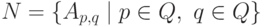 ,
, 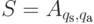 и
и
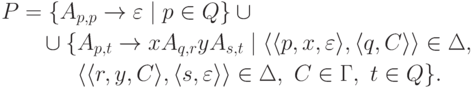
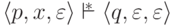 тогда и только тогда, когда
тогда и только тогда, когда 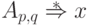 (здесь
(здесь 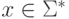 ).
).Пример 10.2.8.
МП-автомат 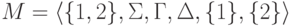 ,
где
,
где  ,
, 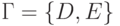 ,
,
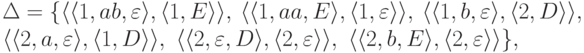
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix @=11mm{
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{ab,\varepsilon:E}
\rloop{0,-1} ^{aa,E:\varepsilon}
\ar "1,2" <0.6mm> ^{b,\varepsilon:D}
& *=[o][F=]{2}
\ar "1,1" <0.6mm> ^{a,\varepsilon:D}
\rloop{0,1} ^{\varepsilon,D:\varepsilon}
\rloop{0,-1} ^{b,E:\varepsilon}
}](/sites/default/files/tex_cache/e69036021e3ea3c488962160adcc730f.png)
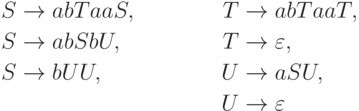
Упражнение 10.2.9. Найти МП-автомат, распознающий язык, порождаемый грамматикой
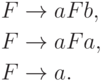
Упражнение 10.2.10. Найти контекстно-свободную грамматику, порождающую язык 
Упражнение 10.2.10. Найти контекстно-свободную грамматику, порождающую язык 
Упражнение 10.2.10. Найти контекстно-свободную грамматику, порождающую язык 
