|
Упражнение 2.1.25 |
Синтаксические моноиды
6.3. Множества двусторонних контекстов
Определение 6.3.1.
Пусть  и
и  .
Тогда множество контекстов
( множество двусторонних контекстов )
слова y относительно языка L
определяется следующим образом:
.
Тогда множество контекстов
( множество двусторонних контекстов )
слова y относительно языка L
определяется следующим образом:
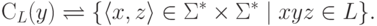
Пример 6.3.2.
Пусть  и
и 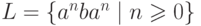 .
Тогда
.
Тогда
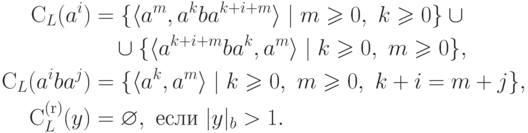
Лемма 6.3.3. Если  , то
, то 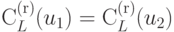 .
.
Доказательство. Из определений следует, что
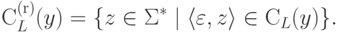
Лемма 6.3.4. Если  , то
, то  и
и  .
.
Доказательство.
Пусть  и
и  .
Тогда
.
Тогда 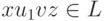 .
Следовательно,
.
Следовательно,  .
Далее,
получаем, что
.
Далее,
получаем, что  ,
,  и
и  .
Второе равенство доказывается аналогично.
.
Второе равенство доказывается аналогично.
Лемма 6.3.5. Если  и
и  , то
, то  .
.
Определение 6.3.6.
Пусть  .
Тогда множество
.
Тогда множество
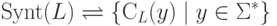
Определение 6.3.7*. Полугруппой
(semigroup)  называется непустое множество M
с ассоциативной бинарной операцией
называется непустое множество M
с ассоциативной бинарной операцией 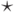 .
.
Определение 6.3.8*.
Пусть 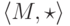 - полугруппа.
Элемент
- полугруппа.
Элемент 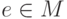 называется единицей
(unit),
если
называется единицей
(unit),
если 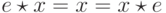 для каждого
для каждого 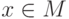 .
.
Определение 6.3.9*. Моноид  - это
полугруппа
- это
полугруппа 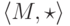 с единицей
с единицей 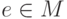 .
.
Теорема 6.3.10*. Определим бинарную операцию на Synt(L) следующим образом:
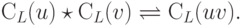
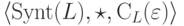 является моноидом.
является моноидом.Теорема 6.3.11. Синтаксический моноид Synt(L) конечен тогда и только тогда, когда язык L является автоматным.
Доказательство
Пусть множество Synt(L)
конечно.
Согласно лемме 6.3.3
множество 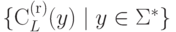 тоже конечно.
В силу леммы 6.1.6
язык L является автоматным.
тоже конечно.
В силу леммы 6.1.6
язык L является автоматным.
Обратно, пусть язык L
распознается некоторым конечным автоматом 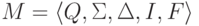 ,
не содержащим переходов с метками длины больше единицы.
Поставим в соответствие
каждому слову y
множество
,
не содержащим переходов с метками длины больше единицы.
Поставим в соответствие
каждому слову y
множество  ,
определенное следующим образом:
,
определенное следующим образом:

 ,
то
,
то  .
Следовательно,
.
Следовательно, 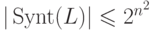 ,
где n = |Q|.
,
где n = |Q|.Пример 6.3.12. Рассмотрим конечный автомат M из примера 2.1.14. Тогда
-
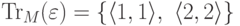 ;
; - если
 ,
то
,
то 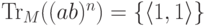 ;
; - если
 ,
то
,
то 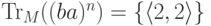 ;
; - если
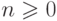 ,
то
,
то 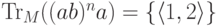 ;
; - если
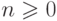 ,
то
,
то 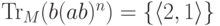 ;
; -
 ;
; -
 .
.
Лемма 6.3.13. Пусть  ,
, 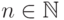 и для каждого слова
и для каждого слова  длины n найдется такое слово
длины n найдется такое слово 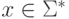 , что
, что  и
и  . Тогда
. Тогда
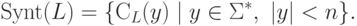
Доказательство.
Индукцией по 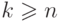 можно доказать, что
для каждого слова
можно доказать, что
для каждого слова  длины k
найдется такое слово
длины k
найдется такое слово 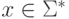 ,
что
,
что  и
и  .
В шаге индукции используется лемма 6.3.5.
.
В шаге индукции используется лемма 6.3.5.
Упражнение 6.3.14. Сколько элементов в синтаксическом моноиде языка a+b над алфавитом {a,b}?
Упражнение 6.3.15. Сколько элементов в синтаксическом моноиде языка b+a+ над алфавитом {a,b}?
Упражнение 6.3.16. Сколько элементов в синтаксическом моноиде языка (aa+b)* над алфавитом {a,b}?
Упражнение 6.3.17. Сколько элементов в синтаксическом моноиде языка (ab)*(ba)*+a* над алфавитом {a,b}?
Упражнение 6.3.18. Сколько элементов в синтаксическом моноиде языка a(b+c)*a(a+b+c)*+b(a+c)*b(a+b+c)*+c(a+b)*c(a+b+c)* над алфавитом {a,b,c}?

