|
Упражнение 2.1.25 |
Дополнительные свойства автоматных языков
4.2*. Локальные языки
Определение 4.2.1.
Гомоморфизм  называется побуквенным (length-preserving),
если |h(a)| = 1
для каждого
называется побуквенным (length-preserving),
если |h(a)| = 1
для каждого 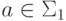 .
.
Замечание 4.2.2.
Гомоморфизм  является побуквенным
тогда и только тогда, когда |h(w)| = |w|
для каждого слова
является побуквенным
тогда и только тогда, когда |h(w)| = |w|
для каждого слова 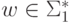 .
.
Определение 4.2.3.
Язык 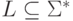 называется локальным,
если существуют такие языки
называется локальным,
если существуют такие языки 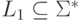 ,
,  ,
, 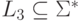 ,
что
,
что
- языки L1 и L2 содержат только однобуквенные слова;
- язык L3 содержит только двухбуквенные слова;
-
 .
.
Лемма 4.2.4. Каждый локальный язык является автоматным.
Очевидно, что языки L1, L2 и L3 в определении 4.2.3 являются конечными. Остается применить замечание 2.1.19 и теоремы 3.1.1 и 3.2.1 (напомним, что разность языков выражается через пересечение и дополнение).
Теорема 4.2.5. Пусть L - язык над алфавитом  и L не содержит пустого слова. Язык L является автоматным
тогда и только тогда, когда
существуют
такие
алфавит
и L не содержит пустого слова. Язык L является автоматным
тогда и только тогда, когда
существуют
такие
алфавит 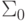 , локальный язык
, локальный язык 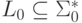 и побуквенный гомоморфизм
и побуквенный гомоморфизм 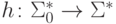 ,
что L = h(L0).
,
что L = h(L0).
Доказательство. Достаточность следует из леммы 4.2.4 и теоремы 4.1.1.
Для доказательства необходимости
рассмотрим конечный автомат  с однобуквенными переходами,
задающий язык L.
В качестве алфавита
с однобуквенными переходами,
задающий язык L.
В качестве алфавита 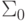 возьмем множество
возьмем множество  .
Положим
.
Положим
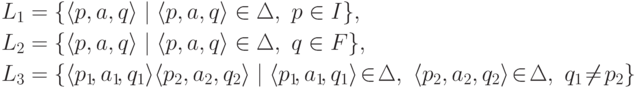
 для каждого
для каждого  .
.Пример 4.2.6.
Пусть 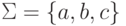 .
Рассмотрим конечный автомат M2
из примера 3.1.3
и обозначим L = L(M2).
Применим конструкцию из доказательства
теоремы 4.2.5
к языку L.
Для удобства заменим
.
Рассмотрим конечный автомат M2
из примера 3.1.3
и обозначим L = L(M2).
Применим конструкцию из доказательства
теоремы 4.2.5
к языку L.
Для удобства заменим 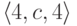 на d,
на d, 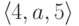 на e
и
на e
и 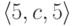 на f.
Получим алфавит
на f.
Получим алфавит 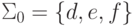 и локальный язык
и локальный язык
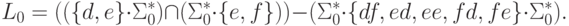

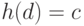 ,
, 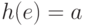 и
и 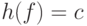 .
Легко проверить, что действительно L = h(L0).
.
Легко проверить, что действительно L = h(L0).Упражнение 4.2.7. Пусть 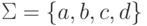 .
Существует ли такой побуквенный гомоморфизм
.
Существует ли такой побуквенный гомоморфизм 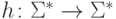 ,
что h(abc) = bac
и h(da) = da?}
,
что h(abc) = bac
и h(da) = da?}
Упражнение 4.2.8. Является ли локальным язык
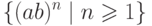
 ?
?Упражнение 4.2.9. Является ли локальным язык

 ?
?Упражнение 4.2.10. Является ли локальным язык
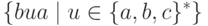
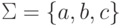 ?
?4.3. Длины слов в автоматных языках
Определение 4.3.1.
Пусть 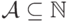 ,
,  и
и  .
Множество
.
Множество  называется заключительно периодическим
(ultimately periodic)
с периодом m,
если выполнено условие
называется заключительно периодическим
(ultimately periodic)
с периодом m,
если выполнено условие
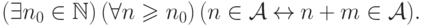
Лемма 4.3.2. Пусть 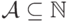 . Тогда равносильны следующие утверждения:
. Тогда равносильны следующие утверждения:
-
множество
 является заключительно периодическим ;
является заключительно периодическим ; -
найдутся такие
положительное целое число m и конечные множества
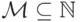 и
и  , что
, что
-
множество
 является объединением конечного семейства арифметических прогрессий.
является объединением конечного семейства арифметических прогрессий.
Теорема 4.3.3. Язык L над однобуквенным алфавитом {a} является автоматным
тогда и только тогда, когда
множество  является заключительно периодическим.
является заключительно периодическим.
Доказательство. Для доказательства необходимости достаточно рассмотреть детерминированный конечный автомат, распознающий язык L.
Теорема 4.3.4. Если язык L является автоматным, то множество 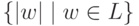 является заключительно периодическим.
является заключительно периодическим.
Доказательство. Рассмотрим конечный автомат, распознающий язык L. Заменим все символы в метках переходов на символ a. Осталось применить теорему 4.3.3 к полученному автоматному языку над однобуквенным алфавитом {a}.
Упражнение 4.3.5.
Существует ли такой автоматный язык L
над алфавитом {a},
что язык 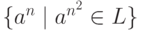 не является автоматным?
не является автоматным?
Упражнение 4.3.6.
Существует ли такой автоматный язык L
над алфавитом {a},
что язык  не является автоматным?
не является автоматным?
Упражнение 4.3.7.
Существует ли такой автоматный язык L1
над алфавитом  ,
что язык
,
что язык
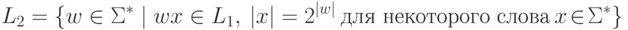
Упражнение 4.3.8.
Существует ли такой
автоматный язык L
над алфавитом {a,b},
что язык 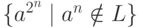 не является автоматным?
не является автоматным?
Упражнение 4.3.9.
Существует ли такой
автоматный язык L
над алфавитом {a,b},
что язык 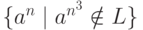 не является автоматным?
не является автоматным?

