|
Упражнение 2.1.25 |
Конечные автоматы
2.4. Характеризация праволинейных языков
Теорема 2.4.1. Каждый автоматный язык является праволинейным.
Без ограничения общности можно предположить,
что исходный язык задан конечным автоматом  ,
где
,
где 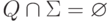 и I = {q0}.
Положим N = Q, S = q0
и
и I = {q0}.
Положим N = Q, S = q0
и

Пример 2.4.2. Язык, распознаваемый конечным автоматом из примера 2.1.2, порождается грамматикой
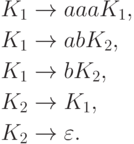
Теорема 2.4.3. Каждый праволинейный язык является автоматным.
Доказательство.
Без ограничения общности можно предположить,
что исходный язык задан праволинейной грамматикой, не содержащей правил
вида  ,
где
,
где 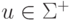 .
Положим Q = N, I = {S},
.
Положим Q = N, I = {S}, 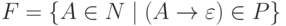 и
и 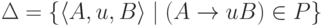 .
.
Пример 2.4.4.
Пусть  .
Рассмотрим грамматику
.
Рассмотрим грамматику
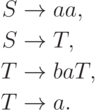
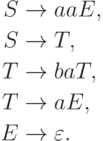
 ,
где Q = {S,T,E}, I = {S}, F = {E}
и
,
где Q = {S,T,E}, I = {S}, F = {E}
и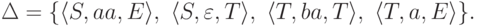
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{S}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" ^{\varepsilon}
\ar "2,2" _{aa}
& *=[o][F-]{T}
\rloop{0,1} ^{ba}
\ar "2,2" ^{a}
\\
%
& *=[o][F=]{E}
}](/sites/default/files/tex_cache/aae96985ab4da43810a8253f4f76cfa0.png)
Упражнение 2.4.5. Найти праволинейную грамматику, порождающую язык 
Упражнение 2.4.6. Существует ли такая праволинейная грамматика G, что язык L(G)R не порождается ни одной праволинейной грамматикой, имеющей столько же правил, сколько грамматика G?
Упражнение 2.4.7. Существует ли такая праволинейная грамматика G, что язык L(G)R не порождается ни одной праволинейной грамматикой с количеством правил n + 1, где n - количество правил в грамматике G?
Упражнение 2.4.8. Существует ли такая праволинейная грамматика G с тремя вспомогательными символами, что язык L(G)R не порождается ни одной праволинейной грамматикой с тремя вспомогательными символами?
2.5.Нормальная форма праволинейных грамматик
Определение 2.5.1. Праволинейная грамматика в нормальной форме
( автоматная грамматика, регулярная грамматика,
finite-state grammar) -
это праволинейная грамматика,
в которой каждое правило имеет вид  ,
, 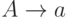 ,
или
,
или  ,
где
,
где 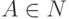 ,
, 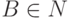 ,
, 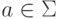 .
.
Теорема 2.5.2. Каждая праволинейная грамматика эквивалентна некоторой праволинейной грамматике в нормальной форме.
Доказательство. Применим последовательно теорему 2.4.3, лемму 2.3.3 и воспользуемся конструкцией из доказательства теоремы 2.4.1.
Теорема 2.5.3. Если праволинейный язык не содержит пустого слова, то он порождается
некоторой праволинейной грамматикой в нормальной форме
без  -правил.
-правил.
Упражнение 2.5.4. Найти праволинейную грамматику, эквивалентную грамматике

Упражнение 2.5.5. Найти праволинейную грамматику в нормальной форме
без  -правил, порождающую язык
-правил, порождающую язык
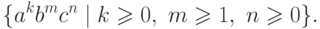
Упражнение 2.5.6. Найти праволинейную грамматику в нормальной форме
без  -правил, порождающую язык
-правил, порождающую язык

