Методы классификации и прогнозирования. Метод опорных векторов. Метод "ближайшего соседа". Байесовская классификация

Решение задачи классификации новых объектов

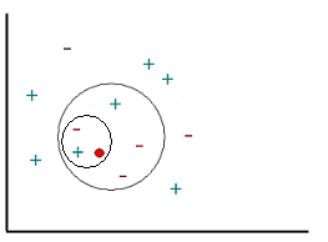
Эта задача схематично изображена на рис. 10.5. Примеры (известные экземпляры) отмечены знаком "+" или "-", определяющим принадлежность к соответствующему классу ("+" или "-"), а новый объект, который требуется классифицировать, обозначен красным кружочком. Новые объекты также называют точками запроса.

Наша цель заключается в оценке (классификации) отклика точек запроса с использованием специально выбранного числа их ближайших соседей. Другими словами, мы хотим узнать, к какому классу следует отнести точку запроса: как знак "+" или как знак "-".

Рис. 10.5. Классификация объектов множества при разном значении параметра k

Для начала рассмотрим результат работы метода k-ближайших соседей с использованием одного ближайшего соседа. В этом случае отклик точки запроса будет классифицирован как знак плюс, так как ближайшая соседняя точка имеет знак плюс.

Теперь увеличим число используемых ближайших соседей до двух. На этот раз метод k-ближайших соседей не сможет классифицировать отклик точки запроса, поскольку вторая ближайшая точка имеет знак минус и оба знака равноценны (т.е. победа с одинаковым количеством голосов).

Далее увеличим число используемых ближайших соседей до 5. Таким образом, будет определена целая окрестность точки запроса (на графике ее граница отмечена красной( серой) окружностью). Так как в области содержится 2 точки со знаком "+" и 3 точки со знаком "-" , алгоритм k-ближайших соседей присвоит знак "-" отклику точки запроса.

Решение задачи прогнозирования

Далее рассмотрим принцип работы метода k-ближайших соседей для решения задачи регрессии. Регрессионные задачи связаны с прогнозированием значения зависимой переменной по значениям независимых переменных набора данных.

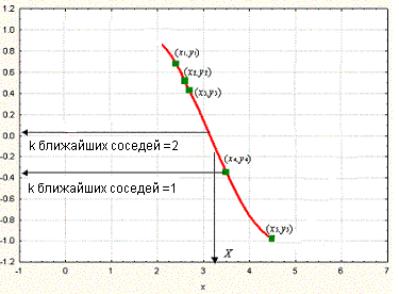
Рассмотрим график, показанный на рис. 10.6. Изображенный на ней набор точек (зеленые прямоугольники) получен по связи между независимой переменной x и зависимой переменной y (кривая красного цвета). Задан набор зеленых объектов (т.е. набор примеров); мы используем метод k-ближайших соседей для предсказания выхода точки запроса X по данному набору примеров (зеленые прямоугольники).

Рис. 10.6. Решение задачи прогнозирования при разных значениях параметра k

Сначала рассмотрим в качестве примера метод k-ближайших соседей с использованием одного ближайшего соседа, т.е. при k, равном единице. Мы ищем набор примеров (зеленые прямоугольники) и выделяем из их числа ближайший к точке запроса X. Для нашего случая ближайший пример - точка (x₄ ;y₄). Выход x₄ (т.е. y₄), таким образом, принимается в качестве результата предсказания выхода X (т.е. Y). Следовательно, для одного ближайшего соседа можем записать: выход Y равен y₄ (Y = y₄ ).

Далее рассмотрим ситуацию, когда k равно двум, т.е. рассмотрим двух ближайших соседей. В этом случае мы выделяем уже две ближайшие к X точки. На нашем графике это точки y₃ и y₄ соответственно. Вычислив среднее их выходов, записываем решение для Y в виде Y = (y₃ + y₄)/2.

Решение задачи прогнозирования осуществляется путем переноса описанных выше действий на использование произвольного числа ближайших соседей таким образом, что выход Y точки запроса X вычисляется как среднеарифметическое значение выходов k-ближайших соседей точки запроса.

Независимые и зависимые переменные набора данных могут быть как непрерывными, так и категориальными. Для непрерывных зависимых переменных задача рассматривается как задача прогнозирования, для дискретных переменных - как задача классификации.

Предсказание в задаче прогнозирования получается усреднением выходов k-ближайших соседей, а решение задачи классификации основано на принципе "по большинству голосов".

Критическим моментом в использовании метода k-ближайших соседей является выбор параметра k. Он один из наиболее важных факторов, определяющих качество прогнозной либо классификационной модели.

Если выбрано слишком маленькое значение параметра k, возникает вероятность большого разброса значений прогноза. Если выбранное значение слишком велико, это может привести к сильной смещенности модели. Таким образом, мы видим, что должно быть выбрано оптимальное значение параметра k. То есть это значение должно быть настолько большим, чтобы свести к минимуму вероятность неверной классификации, и одновременно, достаточно малым, чтобы k соседей были расположены достаточно близко к точке запроса.

Таким образом, мы рассматриваем k как сглаживающий параметр, для которого должен быть найден компромисс между силой размаха (разброса) модели и ее смещенностью.