Язык РЕФАЛ: Рефал-5

Название введенной конструкции " условие " не совсем точно отражает ее смысл: кроме проверки условия, ее результатом является также присваивание значений новым переменным. Часто именно в них и заключен весь смысл условия. Будем содержательно различать 3 вида условий:

1. чистые условия - не определяют новых переменных (как в примере);
2. чистые присваивания - безусловно срабатывают и для этого используются;
3. условные присваивания - смешанный случай.

Рассмотрим другой пример сложения: функция Add складывает два числа, представленные в виде цепочек десятичных цифр, используя функцию сложения двух цифр Ad-digits:

Add {
       (e1 sA) (e2 sB) , <Ad-digits sA sB> : e.Car s.Sum
                    = <Add (<Add (e1) (e2)>) (e.Car)> s.Sum;
       (e1) (e2) = e1 e2;
    };
Ad-digits {
                 '0' sX = sX;
                 sX '0' = sX;
                 '11' = '2';
                 . . .
                 '99' = '18';
          };

Условие в первом предложении содержательно является чистым присваиванием, поскольку, с учетом возможных результатов функции Add-digits, сопоставление всегда выполняется успешно. В результате выполнения условия происходит сложение младших разрядов обоих чисел и результат сложения присваивается: младший разряд - переменной s.Sum, а старший разряд - разряд переноса - переменной e.Car (может иметь пустое значение, которое трактуется как '0'). За счет рекурсивного обращения к функции Add процесс сложения разрядов идет справа налево с добавлением переноса. Как только одно из чисел станет пустым (все его разряды будут сложены с разрядами другого), слева к результату сложения младших разрядов дописывается левая часть, оставшаяся от другого числа. Таким образом, программа демонстрирует экономное сложение столбиком.

Следующий пример демонстрирует возможность использования рекурсии в условиях.

Задача о назначении. Жители поселка N создали несколько общественных 
организаций. Каждый житель может входить в несколько организаций 
или ни в одну. Имеется список членов каждой организации.
Требуется выбрать в каждой организации председателя так, чтобы никто 
не занимал двух постов сразу.

Формально: дан список термов (общественных организаций), каждый из которых есть список символов в скобках (членов организации). Функция Assign должна построить список символов (председателей организаций, в котором все символы различны, и на i -м месте стоит символ из i -го терма. Если построение удастся, то результатом станет этот список в скобках, если же решений нет, то результат - символ '*'.

Для того чтобы решить задачу, сначала ее усложним: сведем ее к функции Assign1, которая имеет еще один аргумент - "запрещенное множество" eZ, т. е. список символов, которые нельзя использовать. Идея состоит в том, что символы, отобранные из части термов, составляют "запрещенное множество" при отборе из другой части.

Assign { eA = <Assign1 () eA>; };
Assign1 {
           (eZ)                                         = (eZ);
           (eZ) (e1 sA e2) eX , <Include (eZ) sA> : F,
                         <Assign1 (eZ sA) eX> : (eR)    = (eR);
           (eZ) eX                                      = ’*’;
        };

В этом решении функция Assign вызывает функцию Assign1 c дополнительным слева пустым списком, который и должна наполнить эта функция. Для его наполнения функция Assign1 во втором своем рефал-предложении исследует очередной терм (очередной организации), и если в этом терме найдется символ sA, не входящий в список sZ (первое условие), то этот символ включается в список вторым условием, но только в том случае, когда такое назначение не помешает назначениям для последующих термов, для чего во втором условии делается рекурсивный вызов Assign1. Если решение задачи существует, то второе рефал-предложение сформирует полностью список sZ и, вызвав первое рефал-предложение, закончит работу благополучно, возвратив список sZ (интерпретация переменной eR может быть любая - например, пустое выражение). Если же решения не существует, то для какого-либо очередного терма не найдется решения во втором рефал-пр едложении, и функция закончит работу, вызвав третье рефал-предложение (возврат символа '*').

Анализ приведенного решения показывает, что здесь имеет место полный перебор возможных назначений: если имеется n организаций по m членов, то трудоемкость алгоритма - . В то же время для такой задачи о назначениях существует алгоритм трудоемкости 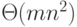. В одном из упражнений предлагается написать такой алгоритм на Рефале-5.

Блок

Другой структурирующей конструкцией Рефала-5 является блок. Он используется в тех случаях, когда несколько рядом стоящих предложений начинаются с одинаковых образцов, либо с одинаковых условий, либо с одинаковых левых частей условий. Такие группы можно объединять в блоки, вынося общее начало "за скобки". Это преобразование может изменить смысл программы. Поэтому следует обратить внимание на семантику блока, которая определяется ниже.

Рассмотрим в качестве примера функцию Merge слияния двух упорядоченных последовательностей в одну упорядоченную последовательность. Используемая при этом функция Compare сравнивает первые термы исходных последовательностей и результатом выдает символ '<', если терм первой последовательности меньше терма второй последовательности; символ '=', если термы равны; и символ '>', если терм первой последовательности больше. Функция Compare используется в условии функции Merge.

Merge {
    (tA e1)(tB e2), <Compare (tA tB)> : '<'
                                   = tA <Merge (e1) (tB e2)>;
    (tA e1)(tB e2), <Compare (tA tB)> : '='
                                   = tA tB <Merge (e1) (e2)>;
    (tA e1)(tB e2), <Compare (tA tB)> : '>'
                                   = tB <Merge (tA e1) (e2)>;
    (e1)(e2) = e1 e2;
      }

В этом примере первые 3 рефал-предложения функции Merge начинаются с одинаковых образцов и одинаковых левых частей условий. Их можно вынести за фигурные скобки блока, оставив в блоке результатные окончания этих предложений.

В общем случае при исполнении блок заменяется на одно из входящих в него окончаний. Вначале делается попытка использовать первое окончание. Но если его исполнение завершается неуспехом, то выбирается второе, и т.д. Если же последнее окончание блока оканчивается неуспехом, то весь блок оканчивается аварийно (в Рефале-6 - неуспехом).

При использовании конструкции блока программа функции Merge станет более наглядной:

Merge {
  (tA e1)(tB e2), <Compare (tA tB)> : {
               '<' = tA <Merge (e1) (tB e2)>;
               '=' = tA tB <Merge (e1) (e2)>;
               '>' = tB <Merge (tA e1) (e2)>;
                 }
  (e1)(e2) = e1 e2;
      }

В общем случае образцовым окончанием называется окончание предложения, начинающееся с образца условия, а последовательность образцовых окончаний, заключенную в фигурные скобки, назовем образцовым блоком . Заметим, что тело функции всегда является образцовым блоком. Для полноты картины в качестве тела функции будем допускать не только блок, но и образцовое окончание, т. е. наружные фигурные скобки могут опускаться, если тело состоит из одного окончания.

В описанном примере мы выделили образцовый блок, который этой структурой не только сделал программу более наглядной, но и сделал ее более эффективной - результатная часть условия вычисляется лишь 1 раз, а затем по очереди сравнивается с образцами образцового блока.

По аналогии с образцовым окончанием и образцовым блоком вводятся результатное окончание и результатный блок. Результатным окончанием называется окончание рефал-предложения, начинающееся с результатного выражения, входящего в условие, а результатным блоком называется последовательность результатных окончаний, заключенная в фигурные скобки. Результатный блок следует применять, когда образцы рефал-предложений одинаковые, а результатные выражения их условий - разные.

Рассмотрим пример определения функции Compset , которая сравнивает 2 множества на включение и возвращает в качестве результата символ '<', если первое множество включено во второе, символ '>', если первое множество включает второе, и символ '?', если ни одно из множеств не включено в другое. При описании будем использовать функцию Diff, которая определяет разность 2 множеств - множество из элементов, входящих в первое множество и не входящих во второе множество. Функцию Compset можно описать следующим образом:

Compset {
  (e1) (e2) , <Diff (e1) (e2)> : = '<';
  (e1) (e2) , <Diff (e2) (e1)> : = '>';
  (e1) (e2) , : = '?';
      }

Все 3 рефал-предложения имеют одинаковые образцы, но результатные части условий у них разные (в третьем предложении оно пустое). Что касается правых образцовых частей условий, то они во всех предложениях пустые. Условие первого предложения выполняется, если разность первого и второго множества пустая, т. е. первое множество включено во второе. Условие второго предложения выполняется, когда второе множество включено в первое. Наконец, условие третьего предложения всегда выполняется: пустой результат сопоставляется с пустым образцом. Так как условия разные, то можно образовать результатный блок, вынеся общий образец всех трех предложений за скобки:

Compset (e1) (e2) , {
       <Diff (e1) (e2)> : = '<';
       <Diff (e2) (e1)> : = '>';
       : = '?';
                    }

Упражнения

1. Разработайте программу на Рефале-5 для задачи о назначениях из раздела 2.17.2 с трудоемкостью алгоритма .
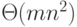2. Разработайте программу Diff на Рефале-5, определяющую разность 2 множеств термов.
3. Разработайте программу на Рефале-5 объединения 2 множеств термов.
4. Разработайте программу на Рефале-5 пересечения 2 множеств термов.
5. Разработайте программу на Рефале-5 сравнения 2 термов, возвращающую один из символов '<', '=' или '>' в зависимости от данных (для чисел - обычное сравнение, для цепочек символов и других термов - лексикографическое сравнение).