Сложные проценты

3.1 Определение сложных процентов

Объясним на простом примере, почему в финансовых расчётах используются не только простые, но и сложные проценты. Предположим, что владелец депозитного счёта, на который начисляется r% простых в год, по истечении каждого года изымает вклад вместе с начисленными процентами и тут же вновь открывает новый депозитный счёт на всю полученную сумму. В результате проценты в каждом следующем году будут начисляться не только на начальную сумму, но и на начисленные в предыдущем году проценты. Через t лет, таким образом, будет накоплена сумма S, равная 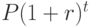, где P - сумма первоначального вклада. Формула

называется формулой сложных процентов для лет. Чтобы не заниматься бессмысленным переоформлением вкладов и иметь возможность вкладывать деньги в длительные проекты, банкиры уже давно стали использовать сложные проценты. Говорят, что Альберт Эйнштейн, открывший миру теорию относительности и считавшийся наиболее оригинальным умом планеты, считал сложный процент одним из чудес этого мира.

Поясним, как получается формула (3.1). В конце первого периода к исходной сумме P прибавляется сумма Pr. Наращенная сумма будет равна:

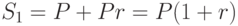
В конце второго периода к имеющейся сумме P(1+r) прибавляется сумма P(1+r)r. Наращенная сумма 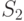составит:

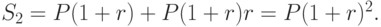
Аналогично, к концу третьего периода будем иметь наращенную сумму

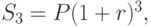
и к концу t -го года наращенная сумма 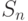будет равна:

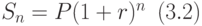
При выводе последней формулы мы считали число лет t целым. Однако в практике финансовых расчётов часто приходится вычислять суммы, наращенные за нецелое число лет, например, за полгода (t=0.5) или за 3 года 2 месяца (t=19/6) и т.п.. Кроме того, процентная ставка r может объявляться для временного промежутка, не равного году, например, квартала или даже дня. Поэтому далее для обозначения временного промежутка, которому соответствует процентная ставка r , мы будем использовать термин период. По определению для произвольного (может быть, и нецелого) числа периодов t наращенная сумма при начислении сложных процентов вычисляется по формуле:

Множитель (1+r) называется множителем наращения. В докомпьютерные времена при финансовых расчётах использовали специально составленные таблицы множителя наращения для различных значений r и t.

Формула (3.2) имеет смысл и при отрицательном значении процента r . В таком случае первоначальная сумма денег P со временем уменьшается. Это уменьшение не всегда носит негативный характер, а может описывать естественный процесс уменьшения ценности, как, например, при амортизации по методу фиксированного процента, о которой речь пойдет в лекции 4.

В формуле (3.2) исходную сумму P называют также текущей или приведенной ценностью (present value) денег, а наращенную сумму S - их будущей ценностью (future value). Используются также связанные с этими названиями обозначения PV и FV, с учётом которых формула (21) принимает вид:

Рис. 5. Сравнение коэффициентов наращения 1+rt и (1+r)^t

При начислении процентов один раз за период при наращенная сумма при сложных процентах больше, чем наращенная сумма при простых процентах, так как верно неравенство:

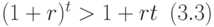
Но при 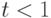неравенство (3.3) меняется на противоположное:

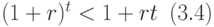
Заметим, что максимальное превышение простого процента над сложным достигается при t=0.5. На рис.5 приведены графики функций и 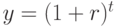, которые наглядно показывают соотношение между коэффициентами наращения при простом и сложном процентах при различных t.

Финансовое учреждение в ряде случаев может указывать процентную ставку на любой период начисления, но для сравнения следует привести такую ставку к годовой. Например, если банк начисляет сложных в месяц, то исходная сумма P за год превратится в наращенную сумму 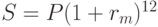. Соответствующая годовая ставка r определяется равенством:

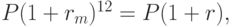
из которого определяем значение r :

Например, если 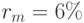, применяя эту формулу, получаем:

Пример 34. Банк начисляет ежегодно 8% сложных. Клиент положил в этот банк 20 000 руб. Какая сумма будет на его счёте через 5 лет?

Решение. Применяя формулу (3.2), находим наращенную сумму S при P=20 000, r=0.08, t=5:

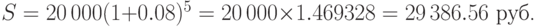
Заметим, что если бы банк выплачивал 8% простых, то через 5 лет на счёте была бы меньшая сумма:

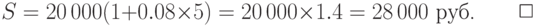
В практике финансовых расчётов ставку сложных процентов, как правило, указывают за период, равный году, но начисление сложных процентов может производиться каждое полугодие, квартал, месяц или даже день. При этом за каждый такой период, равный 1/m части года, начисляются сложные проценты по ставке r/m сложных процентов. В этом случае формула (3.2) примет вид:

где t - длительность промежутка времени, в течение которого начисляются сложные проценты (t измеряется в годах). Например, в случае одного квартала t=0.25.

Чтобы показать, что при годовой ставке сложных процентов r вычисление сложных процентов производится m раз в году по ставке r/m, эту ставку обозначают . Тогда последняя формула принимает вид:

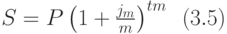
Пример 35. Решим пример (3.5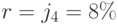) при и при .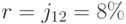

Решение. Применяем формулу при 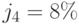, получаем:

Применяем формулу (3.5) при 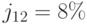, получаем:

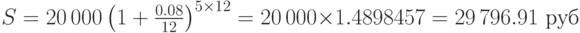
Мы видим, что при увеличении числа периодов начисления процентов при той же годовой процентной ставке наращенная сумма, полученная за одно и то же время, увеличивается.