Анализ возникновения и синтеза систем

7.1. Теория возникновения и синтеза систем.

Термины "возникновение" и "синтез" мы будем понимать, как синонимы, относя первый больше к естественным неживым системам, второй — больше к искусственным системам, оба — к естественным живым системам.

Теория возникновения и синтеза систем (теория ВСС) является развитием теории ОТС применительно к стадии возникновения и синтеза (см. рис. 15а). Предметом исследования теории ВСС являются системы, эволюционирующие от момента появления первых признаков системы (момент t0) до начала стационарного устойчивого функционирования системы (момент tН). Отображение материального объекта-носителя системы в системное пространство М на интервале (t₀, t_Н) должно показывать, что при носитель системы не обладал свойствами, к которым относится функция системы F, и соответствующее, функциональное подпространство пусто. При 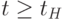носитель, в форме вновь образованной на нем системы, обладает новым свойством-функцией системы, которая, вместе со всеми своими характеристиками, может быть отображена в функциональное подпространство F.

"Кинетика любой системы необходимо должна предшествовать ее структуре" [146].

Применим теорию алгебры логики [46, 131]. Функция системы порождается взаимодействием системы, ее базы и внешней среды (6.9). Это отношение может быть детализировано в системном пространстве М:

.

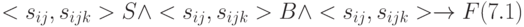Поскольку объединение S, B и V эквивалентно материальному пространству R:

,

то F можно рассматривать как порождение R в границах G:

.

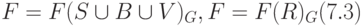Рассматривая в (7.1) все значения s_ijk характеристик s_ij как элементарные высказывания, истинные (1) или ложные (0), мы можем факт существования системы с функцией F оценить функцией алгебры логики f_F:

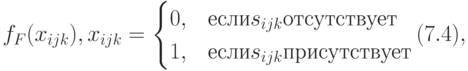
определяемой истинностной таблицей и подчиняющейся аксиомам алгебры логики.

В функциональном подпространстве F_i истинностная функция f_F отображается как одна из характеристик s_ij со значениями s_ijk=0 или 1.

Функция f_F может быть представлена, как показано в (3.2), (3.3), в конъюнктивной и дизъюнктивной нормальной форме:

,

где 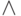— конъюнкция по всем элементам, 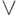— дизъюнкция по всем элементам.

Назовем элементы x_ijk событиями и зададим вероятностную меру (или просто вероятность) функции системы — P_F(a_ijk), удовлетворяющую аксиомам Определения 14. События а_ijk являются элементарными для каждого s_ij и образуют полную систему несовместимых событий:

,

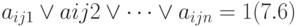т. е. каждая характеристика s может принимать лишь одно значение из n возможных. Тогда вероятность порождения функции системы (7.1) определяется по отношению к независимым характеристикам s_ij:

,

где P(a_ijk) — вероятность элементарного события.

Если какое-либо значение а характеристик системы фиксировано и вероятность этого события , тогда может быть вычислена условная вероятность события а_ijk относительно события а:

P_a(a_ijk)=P(a a_ijk)/P(a) (7.8).

Если все значения характеристик s_ijk имеют условную вероятность относительно каких-то а, то вероятность порождения функции системы, вместо (7.7), будет иметь вид:

Возможна комбинация безусловных (7.7) и условных (7.9) вероятностей, возможно, также, введение условных вероятностей для каждого значения s_ijk.

В функциональном подпространстве F_i вероятность P_F(a_ijk) отображается как одна из характеристик s_ij со значениями s_ijk на отрезке [0, 1].

Проведем интерпретацию отношений порождения системы (7.1), возможность отображения возникновения системы истинностной функцией f_F и вероятностной мерой P_F.

ГИПОТЕЗА 6. Способность материи к организации (также как и к противоположному свойству — дезорганизации) носит случайный характер.

Синтез систем носит вероятностный характер [168, 182].

увеличить изображение
Рис. 24. Вероятностные схемы возникновения систем.

(а) — все элементарные события независимы, (б) — часть элементарных событий независима, другая часть — зависима, (в) — все элементарные события зависимы.

Любая другая альтернатива ГИПОТЕЗЕ 6 не имеет логического начала. В соответствии с ГИПОТЕЗОЙ 6 могут быть рассмотрены 3 вероятностных схемы возникновения систем (рис. 24). Во всех трех схемах система возникает, если f_F=1 и все конъюнкции КНФ, определяющие наличие требуемого значения s_ijk требуемого параметра s_ij системы, истинны. Но в случае (а) система возникает из неорганизованной материи (пример: все естественные неживые системы); в случае (б) система возникает частично из неорганизованной материи, а частично — из уже организованной в форме других систем (пример: все естественные живые системы); в случае (в) система возникает из уже организованной материи в форме других систем (пример: все искусственные системы). Теперь, если в вероятностных схемах заменить f_F на P_F, x_ijk на а_ijk, а реальным объектам приписать наборы постоянных параметров (а₁ ... а_n), то аналогично определяется вероятность возникновения системы: (а) P_F — произведение безусловных вероятностей независимых событий; (б) P_F — произведение безусловных вероятностей независимых событий и условных вероятностей зависимых событий, где условия — параметры (а₁ ... а_n); (в) P_F — произведение условных вероятностей зависимых событий.

В теории эволюции Ч. Дарвина вероятностные переходы — это механизм самоорганизации живых систем в форме естественного отбора. "...Сейчас этот механизм все чаще понимается как универсальный, действующий также и на добиологическом и на постбиологическом (т. е. социальном) уровнях развития материи" [32].

Таким образом, любая живая система имеет вероятность возникновения, сравнимую с 1, только потому, что эта вероятность в основном условная, по отношению к биосфере [111]. Аналогично, вероятность синтеза человеком искусственной системы имеет порядок 1 только потому, что это вероятность условная, по отношению к цивилизации [111]. Сами же вероятности возникновения как биосферы, так и цивилизации очень малы, соответственно, малы и полные вероятности возникновения как живых, так и искусственных систем.

Функция системы F, в соответствии с (6.4), определяется характеристиками своих системообразующих свойств s_ij:

F=F(s_ij) (7.10).

Характеристики s_ij, как мы уже установили, носят случайный характер, а их значения s_ijk образуют полную систему несовместимых событий. Соответственно, функция F является случайной функцией и к ее изучению можно привлекать теорию случайных функций [30].

Случайной функцией будем называть функцию, которая в результате возникновения и синтеза системы может принять тот или иной конкретный вид (внутреннюю функциональную структуру). Конкретный вид случайной функции назовем ее реализацией. Случайная функция характеризуется математическим ожиданием M[F], дисперсией D[F] и другими характеристиками.

Математическое ожидание функции системы — это ее наиболее устойчивое оптимальное выражение. Дисперсия функции системы — это характеристика ориентировочной зоны устойчивости системы и зоны поиска оптимального состояния системы.

Практическим исследованием процессов возникновения и синтеза систем занимаются частно-научные теории: естественных неживых систем - теории астрономии, физики, химии и т. д.; естественных живых систем — теории биологии; искусственных систем — теории соответствующих наук, где синтез осуществляется проектированием.