| Россия, г. Саранск |
Отладка параллельной программы с использованием Intel Thread Checker
Говорят "Любая программа содержит хотя бы одну ошибку". Применительно к параллельному программированию этот тезис можно переформулировать так "Параллельное программирование начинается с параллельных ошибок". Действительно, процесс создания параллельной программы, либо с нуля на основе параллельного алгоритма, либо путем распараллеливания существующей реализации, вносит в разработку программной системы дополнительные сложности, которые неизбежно приводят к появлению дополнительных по сравнению с программированием последовательным ошибок. Конечно, на основе некоторого опыта можно выделить типовые ошибки, встречающиеся в процессе разработки параллельной программы и, вооружившись этим знанием, пытаться в дальнейшем не допускать их, однако на практике… Логика параллельных программ существенно более сложна, чем у программ последовательных. Известно, что поиск ошибки начинается с обнаружения ее наличия. В параллельной программе, характер выполнения которой весьма часто носит "налет" случайности, ошибка может проявляться один раз на сотню и более запусков. Как "поймать" столь неуловимую вестницу беды в программе? Остро необходима инструментальная поддержка процесса отладки.
В настоящей лабораторной работе рассматривается один из инструментов отладки, основанный на сборе и автоматическом анализе информации по результатам выполнения программ и предназначенный для многопоточных и OpenMP программ - Intel® Thread Checker (ITC).
В качестве полигона для демонстрации ошибок и возможностей инструментов по их поиску и анализу используются: классическая задача скалярного умножения векторов; задача Дирихле для уравнения Пуассона, решаемая методом Гаусса-Зейделя; известная задача об обедающих философах и задача "о роботе".
11.1. Методические рекомендации
11.1.1. Цели и задачи работы
Целью данной лабораторной работы является приобретение практических навыков отладки параллельных программ для систем с распределенной памятью, использующих для организации параллелизма либо механизм потоков, либо технологию OpenMP.
Данная цель предполагает решение следующих задач:
- ознакомление с классификацией ошибок, возникающих при разработке многопоточных программ (см. документ "ITC - описание инструмента");
- изучение функциональности инструмента отладки Intel Thread Checker (см. документ "ITC - описание инструмента");
- изучение ряда учебных примеров, направленных на демонстрацию принципов отладки параллельных программ при помощи инструмента отладки Intel Thread Checker;
- самостоятельная разработка и отладка параллельных программ, использующих Windows Threads или технологию OpenMP.
11.1.2. Структура работы
Данный документ состоит из введения, двух разделов, списка дополнительных заданий и списка литературы. Во введении обосновывается актуальность инструментальной поддержки в процессе отладки параллельных программ. В первом разделе приводятся методические рекомендации к лабораторной работе: формулируются цели и задачи, системные требования, рекомендации по проведению занятий. Во втором разделе изучается отладка параллельных программ с демонстрацией характерных ошибок и изучением методов их обнаружения и устранения. Изучение проводится на специально подобранных примерах. Для обнаружения ошибок используется инструмент отладки Intel Thread Checker. В заключение приводятся задания для самостоятельной проработки, а также использованная и рекомендуемая литература.
11.1.3. Системные требования
В документации к ITC [11.2] приводятся следующие системные требования:
11.1.3.1. Аппаратное обеспечение
Минимальные требования
- процессор Pentium® 4;
- ОЗУ 512 Мб;
- свободное дисковое пространство 300 Мб.
При практическом использовании ITС рекомендуются повышенные требования к минимально-необходимым аппаратным ресурсам (для достижения приемлемых показателей оперативности работы):
- процессор Intel® Pentium® 4, поддерживающий технологию Hyper-Threading, или процессор Intel® Xeon®;
- ОЗУ 2 Гб.
Для изучения всех аспектов "реальных" параллельных вычислений желательно использование многоядерных процессоров компании Intel.
11.1.3.2. Программное обеспечение
- Microsoft Windows XP Professional, или Microsoft Windows Server 2003 или Microsoft Windows XP Professional x64 Edition .
- Intel® VTune™ Performance Analyzer версии 7.2 или выше.
- Microsoft Internet Explorer 6.0 или выше.
- Microsoft Visual C++ 6.0 или выше.
- Adobe® Reader®.
Для анализа OpenMP-программ и компиляторной инструментации требуется один из компиляторов:
- Intel® C++ Compiler 8.1 для Windows для архитектуры IA-32, Package ID: w_fc_pc_8.1.023 или выше.
- Intel® C++ Compiler 9.1 для Windows для архитектуры Intel® EM64T.
- Intel® Fortran Compiler для Windows 8.1, Package ID: w_fc_pc_8.1.023 или выше.
11.1.4. Рекомендации по проведению занятий
При выполнении данной лабораторной работы рекомендуется придерживаться следующей последовательности изучения материала:
- Рассмотреть классификацию типовых ошибок при разработке программ, использующих потоки, в том числе OpenMP-программ.
- Получить общее представление об инструменте отладки Intel Thread Checker (см. документ "Описание инструмента").
- Последовательно изучить 4 описанных в данном документе учебных примера, демонстрирующих разные ошибочные ситуации и приемы их диагностики и устранения. При изучении примеров 2-4 по возможности рекомендуется предложить слушателям самостоятельно найти ошибки в приведенных программных реализациях, используя Intel Thread Checker, а затем исправить их.
- Перейти к самостоятельному выполнению слушателями дополнительных заданий.
11.2. Отладка OpenMP и многопоточных программ на примерах
11.2.1. Задача о скалярном произведении векторов
11.2.1.1. Постановка задачи
Задача скалярного умножения векторов отличается простотой математической постановки и очень не сложной программной реализацией (естественно речь идет о последовательной неоптимизированной версии). Вместе с тем, эта задача является алгоритмическим элементом других более трудоемких операций (умножение матрицы на вектор, матричное умножение), да и сама служит хорошим примером, на котором можно демонстрировать большое количество эффектов, появляющихся как при распараллеливании, так и при оптимизации кода.
Итак, пусть имеются вектора  и
и  размерности
размерности  (состоящие из
(состоящие из  элементов).
Скалярным произведением векторов
элементов).
Скалярным произведением векторов  и
и  называется число
называется число  , получаемое как:
, получаемое как:
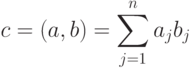
Так, например, при умножении вектора 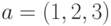 на вектор
на вектор 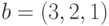 получится, как нетрудно посчитать 10:
получится, как нетрудно посчитать 10:

11.2.1.2. Последовательная реализация
Алгоритм вычисления скалярного произведения полностью описывается его формулой, поэтому приведем сразу его код:
sum_all = 0;
for (i = 0; i < Size; i++)
{
sum_all += x[i] * y[i];
}Необходимые объявления переменных, а также ввод данных здесь рассматривать не будем (см. проект Scalar ).
11.2.1.3 Параллельная реализация 1
Алгоритм скалярного умножения является примером с практически идеальным теоретическим распараллеливанием. Каждая операция умножения компонент векторов может быть выполнена независимо. Единственное "узкое" место - формирование итоговой суммы - может быть легко устранено накоплением результатов в локальных для каждого потока переменных (данных подход демонстрируется в параллельной реализации 2). Однако на практике получить при расчете скалярного произведения хорошие показатели ускорения весьма непросто в силу чрезвычайной легковесности операции в распараллеливаемом цикле. Поскольку в данный момент нас интересует лишь создание работоспособной параллельной версии (с использованием ITC при необходимости), поэтому вопросы производительности мы затрагивать не будем.
Итак, мы имеем цикл с регулярной структурой и одинаковой вычислительной сложностью итераций. Распараллеливание его средствами OpenMP не представляет никакого труда.
sum_all = 0;
#pragma omp parallel for
for (i = 0; i < N; i++)
{
sum_all += up[i] * vp[i];
}Некоторый произвол возможен в том, как разделить вычисления между потоками. Первая схема - каждый поток обрабатывает непрерывный фрагмент умножаемых векторов. Вторая - вектора делятся между потоками поэлементно (или поблочно). Каждая схема может быть реализована с использованием параметра schedule. Провести соответствующие эксперименты предоставляем читателю самостоятельно.
В представленном выше коде мы сознательно допустили достаточно очевидную ошибку. Посмотрим, как с ней справится ITC.
11.2.1.4. Анализ параллельной реализации 1
Откройте проект Scalar, последовательно выполняя следующие шаги:
- запустите приложение Microsoft Visual Studio 2005,
- в меню File выполните команду Open
 Project/Solution…,
Project/Solution…, - в диалоговом окне Open Project выберите папку C:\ITCLabs\Scalar,
- дважды щелкните на файле Scalar.sln или, выбрав файл, выполните команду Open.
После открытия проекта в окне Solution Explorer дважды щелкните на файле исходного кода Scalar.сpp. После этих действий программный код, с которым предстоит работать, будет открыт в редакторе кода Microsoft Visual Studio 2005.
Далее выполните действия, описанные в пункте 7.3 документа "ITC - Краткое описание.doc", чтобы подготовить программу для анализа в ITC.
И, наконец, запустите ITC, создайте в нем новый проект и укажите путь к исполняемому файлу C:\ITCLabs\Scalar\Debug\Scalar.exe.
Нажмите кнопку Finish. После этого запустится ITC, произведет инструментацию программы и начнет анализ. Результатом станет появление следующей диагностики:
Как и следовало ожидать источник неприятностей - переменная sum_all, на что недвусмысленно указывает ITC, сигнализируя о гонке данных при работе с этой переменной.
Для исправления представленного выше кода требуется лишь одна модификация - переменная, в которую накапливается сумма, должна быть сделана локальной для каждого потока. В противном случае во избежание конфликта доступа придется заключать операцию суммирования в критическую секцию, что сведет эффект от распараллеливания к нулю. Естественно по окончании работы потоков необходимо собрать из локальных сумм общий результат. Реализовать эту схему в OpenMP можно различными способами, рассмотрим наиболее быстрый вариант, использующий параметр reduction директивы parallel for.
Вносим исправления:
sum_all = 0;
#pragma omp parallel for reduction(+:sum_all)
for (i = 0; i < N; i++)
{
sum_all += up[i] * vp[i];
}Повторно запускаем активность в ITC и убеждаемся в отсутствии ошибок:
Отметим, что параметр reduction(+:sum_all) решает обе заявленные выше задачи (локализации переменной суммирования и подсчета итоговой суммы) и это наиболее короткий из возможных вариантов.
11.2.1.5. Параллельная реализация 2
В дополнение рассмотрим еще один несколько искусственный вариант скалярного умножения, который, тем не менее, позволит нам продемонстрировать некоторые типичные ошибки, нередко допускаемые при создании OpenMP программ.
Итак, пусть параллельная схема вычисления скалярного произведения выглядит следующим образом.
#pragma omp parallel private(rank, sum)
{
rank = omp_get_thread_num();
if (rank == 0)
{
NumThreads = omp_get_num_threads();
x = CreateVector(N);
y = CreateVector(N);
}
sum[rank] = 0;
#pragma omp for
for (i = 0; i < N; i++)
{
sum[rank] += x[i] * y[i];
}
}
sum_all = 0;
for (i = 0; i < NumThreads; i++)
{
sum_all += sum[i];
}
DeleteVector(x);
DeleteVector(y);Нулевой поток "занимается" выделением памяти под данные и их инициализацией, после чего начинается собственно расчет. Представленная схема хоть и выглядит для задачи скалярного умножения чересчур усложненной, но в других ситуациях вполне может с успехом применяться. Отметим также, что здесь использовано другое решение для локализации суммы в потоках - массив sum.
Попробуйте самостоятельно найти в представленном коде ошибки, прежде чем мы перейдем к анализу.