Моделирование ситуаций и разработка решений

8.3.5. Характеристика способов принятия решений на основе стохастического факторного анализа

Способы принятия решений на основе стохастического факторного анализа применяются при решении многих задач управления хозяйственной деятельностью, осуществляемых в условиях неопределенности.

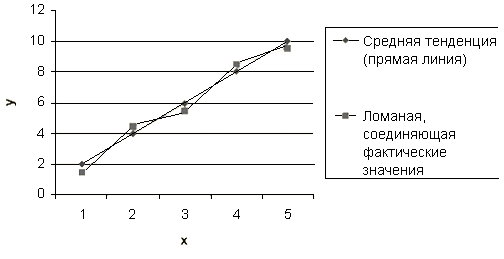
Рассмотрим простейшую зависимость между результирующим экономическим показателем Y и воздействующим фактором Х (рис. 8.3).

Рис. 8.3. Простейшая зависимость между результирующим экономическим показателем Y и воздействующим фактором Х

Для принятия управленческих решений требуется получение ответа на следующие вопросы:

1. влияет ли тот или иной фактор X на управляемый результирующий показатель Y?
2. каковы степень и характер влияния X на Y, определяющий вид их взаимосвязи (линейная или нелинейная, возрастающая или убывающая зависимость)?
3. каков уровень доверия к полученным модельным зависимостям Y от X?
4. как можно спрогнозировать изменение результата y при возможном изменении значения фактора X?

На все эти и другие вопросы дает ответы корреляционно-регрессионный анализ.

Простейшую зависимость показателя Y от фактора X выражает линейная однофакторная модель вида:

,

Разница между фактическим значением показателя y_i при фиксированном x_i и расчетным значением детерминированной основы y_ip, именуемая случайной компонентой (остатком), определяется соотношением:

.

Расчетные значения y_ip находятся на линии регрессии, а фактические значения y_i располагаются в некоторой области, прилегающей к этой линии (рис. 8.4).

Рис. 8.4. Пример построения однофакторной линейной регрессионной модели

Задача получения уравнения регрессии состоит в нахождении на основе пар наблюдений (x_i, y_i) таких значений коэффициентов a₀ и a₁, при которых линия регрессии пройдет максимально близко к точкам фактических наблюдений.

Наилучшим способом нахождения коэффициентов уравнения регрессии является метод наименьших квадратов, разработанный Гауссом и Лежандром, суть которого заключается в нахождении коэффициентов a₀ и a₁ для которых сумма квадратов разностей между фактическими значениями показателя y_i и расчетными y_ip, лежащими на линии регрессии, минимальна .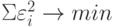

Показателем, характеризующим качество модели, может служить коэффициент детерминации:

.

Он характеризует ту долю совокупной (общей) дисперсии 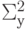, которая объясняется с помощью регрессионной модели. При R² = 1 все значения выборки лежат на линии регрессии. При R² = 0 уравнение регрессии ничего не объясняет.