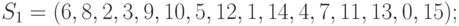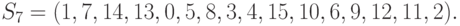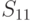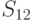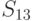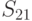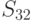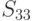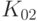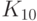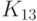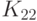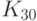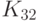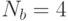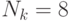НОУ ИНТУИТ | Криптографические методы защиты информации. Лекция 7: Современные симметричные алгоритмы шифрования

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 02.03.2017 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать программу

7.4 Шифр "Магма" ГОСТ Р 34.12-2015

В июне 2015 года приняты два новых криптографических стандарта Российской Федерации: ГОСТ Р 34.12-2015 "Информационная технология. Криптографическая защита информации. Блочные шифры" и ГОСТ Р 34.13-2015 "Информационная технология. Криптографическая защита информации. Режимы работы блочных шифров", которые вступают в действие с 1 января 2016 года.

ГОСТ Р 34.12-2015 содержит описание двух блочных шифров с длинами блока 128 и 64 бит. Шифр ГОСТ 28147-89 с зафиксированными блоками нелинейной подстановки включен в новый ГОСТ Р 34.12-2015 в качестве 64-битового шифра под названием "Магма" ("Magma"). Стандартом определены следующие блоки замен:

S_0 = (12, 4, 6, 2, 10, 5, 11, 9, 14, 8, 13, 7, 0, 3, 15, 1);

S_1 = (6, 8, 2, 3, 9, 10, 5, 12, 1, 14, 4, 7, 11, 13, 0, 15);

S_2 = (11, 3, 5, 8, 2, 15, 10, 13, 14, 1, 7, 4, 12, 9, 6, 0);

S_3 = (12, 8, 2, 1, 13, 4, 15, 6, 7, 0, 10, 5, 3, 14, 9, 11);

S_4 = (7, 15, 5, 10, 8, 1, 6, 13, 0, 9, 3, 14, 11, 4, 2, 12);

S_5 = (5, 13, 15, 6, 9, 2, 12, 10, 11, 7, 8, 1, 4, 3, 14, 0);

S_6 = (8, 14, 2, 5, 6, 9, 1, 12, 15, 4, 11, 0, 13, 10, 3, 7);

S_7 = (1, 7, 14, 13, 0, 5, 8, 3, 4, 15, 10, 6, 9, 12, 11, 2).

Приведенный в стандарте набор S-блоков обеспечивает наилучшие характеристики, определяющие стойкость криптоалгоритма к дифференциальному и линейному криптоанализу.

Фиксация блоков нелинейной подстановки сделает алгоритм ГОСТ 28147-89 более унифицированным и исключает использование "слабых" блоков нелинейной подстановки. Кроме того, фиксация в стандарте всех долговременных параметров шифра отвечает принятой международной практике. Новый стандарт ГОСТ Р 34.12-2015 терминологически и концептуально связан с международными стандартами ИСО/МЭК 10116 "Информационные технологии. Методы обеспечения безопасности. Режимы работы для n-битовых блочных шифров" (ISO/IEC 10116:2006 Information technology -- Security techniques - Modes of operation for an n-bit block cipher) и серии ИСО/МЭК 18033 "Информационные технологии. Методы и средства обеспечения безопасности. Алгоритмы шифрования": ИСО/МЭК 18033-1:2005 "Часть 1. Общие положения" (ISO/IEC 18033-1:2005 Information technology -- Security techniques -- Encryption algorithms -- Part 1: General) и ИСО/МЭК 18033-3:2010 "Часть 3. Блочные шифры" (ISO/IEC 18033-3:2010 (Information technology -- Security techniques -- Encryption algorithms – Part 3: Block ciphers).

В стандарт ГОСТ Р 34.12-2015 включен также новый блочный шифр ("Кузнечик") с размером блока 128 бит,см.ниже. Ожидается, что этот шифр будет устойчив ко всем известным на сегодняшний день атакам на блочные шифры.

7.5 Блочный шифр Rijndael

Блочный шифр Rijndael в октябре 2000 года стал победителем проведенного Национальным Институтом Стандартов и Технологий (NIST) США конкурса на замену признанного ненадежным алгоритма шифрования DES (Data Encryption Standart). В феврале 2001 года прошел через открытое обсуждение и в апреле 2001 года был объявлен новым федеральным стандартом шифрования США AES (Advanced Encryption Standart), см. [4].

Алгоритм шифрования Rijndael имеет переменную длину блоков и различные длины ключей. Длина ключа и длина блока могут быть равны независимо друг от друга 128, 192 или 256 битам. В стандарте AES определена длина блока данных, равная 128 битам.

Промежуточные результаты преобразований, выполняемых в рамках крипто-алгоритма, называют состояниями (State). Состояние можно представить в виде прямоугольного массива байтов.

При размере блока, равном 128 битам, этот 16-байтовый массив (таблицы 7.5, 7.6) имеет 4 строки и 4 столбца (каждая строка и каждый столбец в этом случае могут рассматриваться как 32-разрядные слова). Входные данные для шифра обозначаются как байты состояния в порядке $S_{00}, S_{10}, S_{20}, S_{30}, S_{01}, S_{11}, \ldots$ .

После завершения действия шифра выходные данные получаются из байтов состояния в том же порядке. В общем случае число столбцов равно длине блока, деленной на 32.

В таблице 7.5 представлен пример 128-разрядного блока данных в виде массива state.

Ключ шифрования также представлен в виде прямоугольного массива с четырьмя строками (таблица 7.6. Число столбцов этого массива равно длине ключа, деленной на 32. В стандарте определены ключи всех трех размеров ---128 бит, 192 бита и 256 бит, то есть соответственно 4, 6 и 8 32-разрядных слова (или столбца --- в табличной форме представления). В некоторых случаях ключ шифрования рассматривается как линейный массив 4-байтовых слов. Слова состоят из 4 байтов, которые находятся в одном столбце (при представлении в виде прямоугольного массива).

Зависимость числа раундов 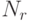N_r в алгоритме Rijndael от чисел N_b и N_k 32-битных слов, соответственно, в блоке и ключе, отражена в таблице 7.7.

Таблица 7.5. Схема представления 128-разрядного блока данных в виде матрицы состояния
$S_{00}$	$S_{01}$	$S_{02}$	$S_{03}$
$S_{10}$	$S_{11}$	$S_{12}$	$S_{13}$
$S_{20}$	$S_{21}$	$S_{22}$	$S_{23}$
$S_{30}$	$S_{31}$	$S_{32}$	$S_{33}$

Таблица 7.6. Схема представления 128-разрядного ключа в виде матрицы состояния
$K_{00}$	$K_{01}$	$K_{02}$	$K_{03}$
$K_{10}$	$K_{11}$	$K_{12}$	$K_{13}$
$K_{20}$	$K_{21}$	$K_{22}$	$K_{23}$
$K_{30}$	$K_{31}$	$K_{32}$	$K_{33}$

Таблица 7.7. Зависимость числа раундов алгоритма от длины блока и ключа

10	12	14
12	12	14
14	14	14

7.5.1 Раундовое преобразование

Раунд состоит из четырех различных преобразований:

замена байтов SubBytes() --- побайтовая подстановка в S-блоках с фиксированной таблицей замен размерностью 8x256;
сдвиг строк ShiftRows() --- побайтовый сдвиг строк массива State на различное количество байт;
перемешивание столбцов MixColumns() --- умножение столбцов состояния, рассматриваемых как многочлены над $GF(2^{8})$ , на многочлен третьей степени g(x) по модулю $x^{4}+1$ ;
сложение с раундовым ключом AddRoundKey() --- поразрядное XOR с текущим фрагментом развернутого ключа.

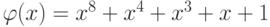Алгоритм Rijndael оперирует байтами, которые рассматриваются как элементы конечного поля $GF(2^{8})$ . Для построения такого поля используется неприводимый многочлен 8-й степени над полем $\mathbb{Z}_2$ (см. параграф 1.12). В алгоритме Rijndael используется многочлен $\varphi (x)=x^{8 }+x^{4 }+x^{3 }+ x+ 1$ .

Для каждого байта $b=b_0 + b_1 \cdot 2 + \ldots + b_7 \cdot 2^7$ построим многочлен $A_b(x)=b_0 + b_1 x + \ldots +b_7 x^7$ , который можно считать элементом построенного нами поля GF(2^8) . Далее отождествим следующие представления байта:

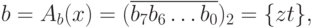
$b=A_b(x) = (\overline{b_7 b_6\ldots b_0})_2 = \{zt\},$

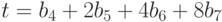где z=b_0+2b_1+4b_2+8b_3 , t = b_4+2b_5+4b_6+8b_7 --- цифры шестнадцатеричного представления байта.

Операция сложения над элементами поля представляет собой поразрядное сложение по модулю 2, умножение представляет собой операцию умножения со взятием результата по модулю многочлена $\varphi$ .

Преобразование SubBytes() представляет собой нелинейную замену байтов, выполняемую независимо с каждым байтом состояния.

построим многочлен , найдём к нему обратный многочлен $B(x)=A_b(x)^{-1} ~(\mod \varphi(x) )$ , и составим новый байт 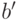из коэффициентов ;
получим байт с помощью линейного преобразования:

$\left(\begin{array}{c} b_0'' \\ b_1'' \\ b_2'' \\ b_3'' \\ b_4'' \\ b_5'' \\ b_6'' \\ b_7'' \end{array}\right)=\left( \begin{array}{cccccccc} 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \end{array} \right)\cdot \left(\begin{array}{c} b_0' \\ b_1' \\ b_2' \\ b_3' \\ b_4' \\ b_5' \\ b_6' \\ b_7' \end{array}\right)+\left(\begin{array}{c} 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ \end{array}\right)$

Пример 7.8 Применим преобразование SubBytes() к байту $\{83\}$ .

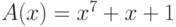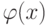Многочлен, коэффициентами которого являются биты данного числа: A(x) = x^7 + x + 1 . Вначале найдём обратный к нему многочлен относительно умножения в поле $GF(2^{8})$ . Как уже отмечалось ранее, операция умножения в поле $GF(2^{8})$ является операцией умножения многочленов с взятием результата по модулю неприводимого многочлена $\varphi(x)$ восьмой степени с использованием операции XOR (сложения по модулю 2) при приведении подобных членов. 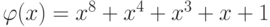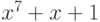Так как авторами алгоритма шифрования Rijndael был выбран неприводимый многочлен $\varphi (x)=x^{8}+x^{4}+x^{3}+x+1$ , то нам необходимо найти такой многочлен $B(x)=A^{-1}(x)$ , который бы при умножении на многочлен $x^{7}+x+1$ по модулю 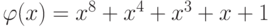$\varphi (x) = x^{8}+x^{4}+x^{3}+x+1$ давал единицу, то есть $(x^{7}+x+1)\cdot B(x)=1 (\mod (x^{8}+x^{4}+x^{3}+x+1))$ .

С помощью расширенного алгоритма Евклида находим:

$1=x^7\cdot A(x) + (x^6 + x^2 + x + 1)\cdot \varphi(x).$

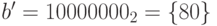Отсюда $B(x) = A^{-1}(x) = x^7$ . Соответствующий байт: $b'=1000 0000_2 = \{80\}$ .

Теперь совершим второй этап преобразования.

$\left(\begin{array}{c} b_0'' \\ b_1'' \\ b_2'' \\ b_3'' \\ b_4'' \\ b_5'' \\ b_6'' \\ b_7'' \end{array}\right)=\left( \begin{array}{cccccccc} 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \end{array} \right)\cdot \left(\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{array}\right)+\left(\begin{array}{c} 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ \end{array}\right)= \left(\begin{array}{c} 0 \\ %11101100 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \end{array}\right).$

Результатом проведенного преобразования является значение 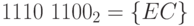$1110\ 1100_2=\{EC\}$ .

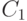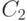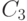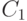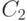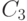Преобразование сдвига строк ShiftRows() выглядит следующим образом: последние 3 строки состояния циклически сдвигаются влево на различное число байтов. Строка 1 сдвигается на C_1 байт, строка 2 --- на C_2 байт, и строка 3 --- на C_3 байт. Значение сдвигов C_1 , C_2 и C_3 в Rijndael зависят от длины блока N_b . Их величины приведены в таблице 7.8.

Таблица 7.8. Величины сдвигов строк состояния при выполнении операции


1	2	3	1	2	3	1	3	4

В стандарте AES, где определен единственный размер блока, равный 128 битам, C_1=1 , C_2=2 , C_3=3 .

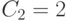Преобразование перемешивания столбцов (MixColumns) действует отдельно на каждом -м столбце таблицы состояния, как линейное преорбазование:

$\begin{equation}\left(\begin{array}{c} S'_{0,i} \\ S'_{1,i} \\ S'_{2,i} \\ S'_{3,i} \end{array}\right)= \left(\begin{array}{cccc} \{02\} & \{03\} & \{01\} & \{01\} \\ \{01\} & \{02\} & \{03\} & \{01\} \\ \{01\} & \{01\} & \{02\} & \{03\} \\ \{03\} & \{01\} & \{01\} & \{02\} \\ \end{array}\right)\cdot \left(\begin{array}{c} S_{0,i} \\ S_{1,i} \\ S_{2,i} \\ S_{3,i} \end{array}\right), \end{equation}$

( 7.2)

$\{02\}=x, \qquad \{03\}=x+1, \qquad \{01\}=1.$

В результате такого умножения байты 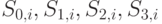$S_{0,i}, S_{1,i}, S_{2,i}, S_{3,i}$ заменятся, соответственно, на байты

$S'_{0,i} = x\cdot S_{0,i} + (x+1)\cdot S_{1,i} + S_{2,i} + S_{3,i},$

( 7.3)

$S'_{1,i} = S_{0,i} + x\cdot S_{1,i} + (x+1)\cdot S_{2,i} + S_{3,i},$

( 7.4)

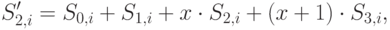$S'_{2,i} = S_{0,i} + S_{1,i} + x\cdot S_{2,i} + (x+1)\cdot S_{3,i},$

( 7.5)

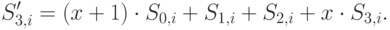$S'_{3,i} = (x+1)\cdot S_{0,i} + S_{1,i} + S_{2,i} + x\cdot S_{3,i}.$

( 7.6)

Применение этой операции ко всем четырем столбцам состояния обозначают через MixColumns().

Пример 7.9 Применим операцию MixColumns() к столбцу: $S_{0,0}=\{2d\}$ , $S_{1,0}=\{26\}$ , $S_{2,0}=\{31\}$ , $S_{1,0}=\{4c\}$ .

Представим элементы $S_{i,0}$ полиномами:

$S_{0,0}=\{2d\}=x^5+x^3+x^2+1,\qquad S_{1,0}=\{26\}=x^5+x^2+x,\\S_{2,0}=\{31\}=x^5+x^4+1,\qquad S_{3,0}=\{4c\}=x^6+x^3+x^2.$

Находим $S_{0,0}$ по формулам (7.3)-(7.6). Вычислим многочлен:

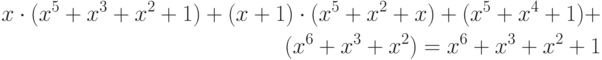
$\begin{align*}x\cdot (x^5+x^3+x^2+1) + (x+1)\cdot (x^5+x^2+x) + (x^5+x^4+1) + \\(x^6+x^3+x^2) = x^6+x^3+x^2+1\end{align*}$

и возьмём остаток от его деления на 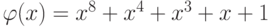$\varphi(x)=x^8 + x^4 + x^3 + x + 1$ . Имеем:

$S'_{0,0} = x^6+x^3+x^2+1 ~(\mod \varphi(x) ) = \{4d\}.$

Аналогично находим остальные компоненты столбца:

$\begin{align*}S'_{1,0}=(x^5+x^3+x^2+1) + x\cdot (x^5+x^2+x) + (x+1)(x^5+x^4+1) + \\ (x^6+x^3+x^2) = x^6+x^5+x^4+x^3+x^2+x \equiv \\ \equiv x^6+x^5+x^4+x^3+x^2+x ~(\mod \varphi(x) ) = \{7e\},\end{align*} % \begin{align*}S'_{2,0}=(x^5+x^3+x^2+1) + (x^5+x^2+x) + x\cdot (x^5+x^4+1) + \\ (x+1)\cdot (x^6+x^3+x^2) = x^7+x^5+x^4+x^3+x^2+1 \equiv \\ \equiv x^7+x^5+x^4+x^3+x^2+1 ~(\mod \varphi(x) ) = \{bd\}, \end{align*} % \begin{align*}S'_{3,0}=(x+1)\cdot (x^5+x^3+x^2+1) + (x^5+x^2+x) + (x^5+x^4+1) + \\ x\cdot (x^6+x^3+x^2) = x^7 + x^6 + x^5 + x^4 + x^3 \equiv\\ \equiv x^7 + x^6 + x^5 + x^4 + x^3 ~(\mod \varphi(x) ) = \{f8\}. \end{align*}$

На рисунке 7.5 показано преобразование исходного столбца 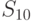$S_{10}$ в столбец $S_{10}'$ с помощью операции MixColumns().

Рис. 7.5. Применение MixColumns() к столбцу состояния

В операции добавления подключа (AddRoundKey) подключ $K^{(r)}$ раунда добавляется к данным с помощью операции побитового сложения по модулю два (операция XOR). Это сложение также можно рассматривать как сложение элементов поля GF(2^8) :

$S'_{ij} = S_{ij} + K^{(r)}_{ij}.$

7.5.2 Алгоритм выработки раундовых ключей

Подключи вырабатываются из исходного секретного ключа шифрования с помощью алгоритма выработки ключей (Key Schedule). Длина подключа (в 32-разрядных словах) равна длине блока N_b слов.

Подключи, используемые в каждом раунде шифрования, получаются из исходного секретного ключа шифрования с помощью алгоритма выработки подключей. Он содержит два компонента.

Расширение ключа (Key Expansion). В результате расширения из ключа длиной слов получается расширенный ключ, слова которого обозначим через $w[i], i=0,1,\ldots,N_k\cdot (N_r+1)-1$ .
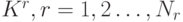Выбор раундовых подключей из расширенного ключа. В результате получаются раундовые ключи $K^{r}, r=1,2\ldots, N_r$ .

Расширение ключа. При расширении ключа нам потребуются следующие операции, применяемые к словам , состоящим из байт v_0, v_1, v_2, v_3 (будем использовать обозначение $v=\{v_0,v_1,v_2,v_3\}$ ):

$\begin{align*}\text{RotWord}(\{v_0,v_1,v_2,v_3\}) = \{v_1,v_2,v_3,v_0\},\\ \text{SubWord}(\{v_0,v_1,v_2,v_3\}) = \{\text{SubBytes}(v_0),\text{SubBytes}(v_1),\\ \text{SubBytes}(v_2),\text{SybBytes}(v_3)\}. \end{align*}$

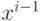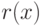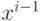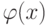Кроме того, определим константы-слова $\text{Rcon}[i]=\{x^{i-1}, 0, 0, 0\}$ . Напомним, что под байтом $x^{i-1}$ понимается элемент поля GF(2^8) , то байт состоит из коэффициентов из $\mathbb{Z}_2$ остатка r(x) от деления $x^{i-1}$ на неприводимый многочлен $\varphi(x)$ .

Под сложением слов u+v будем понимать их побитовое сложение по модулю два, что эквивалентно побайтовому сложению в поле GF(2^8) . Иногда также пишут $u\ \text{XOR}\ v$ .

Первые слова $w[0], w[1],\ldots, w[N_k-1]$ расширенного ключа совпадают со словами ключа шифрования. Последующие слова w[i] вычисляются последовательно при $i=N_k, N_k+1,\ldots$ по следующему алгоритму:

Возьмём .
Если кратно и $N_k\leq 6$ , то положим $v:=\text{SubWord}(\text{RotWord}(v)) + \text{Rcon}[i]$ .
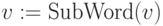Если и $i\equiv 4 ~(\mod N_k)$ , то положим $v:=\text{SubWord}(v)$ .
Положим .

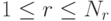Выбор раундовых подключей. Ключ $K^{(r)}$ -го раунда ( $1\leq r\leq N_r$ ) состоит из слов $w[N_b\cdot i], w[N_b\cdot i + 1], \ldots w[N_b\cdot (i+1)-1]$ . Например, при N_b = 4 получаем:

$w=\{w[0],w[1],w[2],w[3], \underbrace{w[4],w[5],w[6],w[7]}_{\text{Подключ} K^{(1)}}, \underbrace{w[8],w[9],w[10],w[11]}_{\text{Подключ} K^{(2)}},\ldots \}.$

7.5.3 Дополнение. О выборе блоков замен для AES и аналогичных алгоритмов

Как известно, для оценки качества блоков замен используются различные критерии. Одним из таких критериев является максимум модуля коэффициентов корреляции, имеет значение также количество нулей корреляционной матрицы. Для выбранного в алгоритме Rijndael неприводимого многочлена $\varphi(x)=x^{8}+x^{4}+x^{3}+x+1$ корреляционная матрица следующая:

$\begin{scriptsize} \left( \begin{array}{cccccccc} -0,0469&0,0625&0,0313&-0,0156&-0,0938&-0,0156&0,0938&-0,0938\\ 0,0625&0,0938&-0,0625&-0,0938&-0,1094&0,0156&0&0,0781\\ 0,0313&-0,0625&-0,0938&-0,0469&0,0156&0&0,0781&0,0625\\ -0,0156&-0,0938&-0,0469&-0,0625&0,0625&-0,0625&-0,0625&0,1250\\ -0,0938&-0,1094&0,0156&0,0625&0,0938&0,0469&0,0313&-0,0156\\ -0,0156&0,0156&0&-0,0625&0,0469&-0,0313&-0,0156&-0,0938\\ 0,0938&0&0,0781&-0,0625&-0,0313&-0,0156&-0,0938&-0,0156\\ -0,0938&0,0781&0,0625&0,1250&-0,0156&-0,0938&-0,0156&0,0938 \end{array} \right) \end{scriptsize}$

Заметим, что за счет выбора другого неприводимого многочлена степени 8 над полем GF(2^8) можно получить корреляционную матрицу с бОльшим количеством нулевых элементов, что затруднит корреляционный криптоанализ, однако упростит аппроксимацию шифра аффинными булевыми функциями за счет большего количества единичных значений элементов в полной матрице коэффициентов корреляции со всеми аффинными функциями.

Пример 7.10 Применение полинома (десятичный эквивалент) 355 наиболее затруднит аппроксимацию шифра аффинными булевыми функциями, а применение полинома 425 наиболее затруднит корреляционный криптоанализ, однако упростит аппроксимацию аффинными булевыми функциями.

В таблице 7.9 приведен пример оптимального по корреляционному критерию блока замен длины 256 [5].

Таблица 7.9. Пример блока замен длины 256
	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	5C	58	04	F2	02	F9	A1	AE	F6	05	AB	AA	57	5D	F1	0F
1	A9	A3	0D	F5	06	F3	5F	5E	FA	07	5B	54	AC	A8	F0	00
2	B8	BC	12	E4	19	E2	4E	41	E5	16	4A	4B	BD	B7	EF	11
3	43	49	15	ED	13	E6	BE	BF	E7	1A	B4	BB	48	4C	E0	10
4	98	9C	32	C4	39	C2	6E	61	C5	36	6A	6B	9D	97	CF	31
5	63	69	35	CD	33	C6	9E	9F	C7	3A	94	9B	68	6C	C0	30
6	7C	78	24	D2	22	D9	81	8E	D6	25	8B	8A	77	7D	D1	2F
7	89	83	2D	D5	26	D3	7F	7E	DA	27	7B	74	8C	88	D0	20
8	D8	DC	72	84	79	82	2E	21	85	76	2A	2B	DD	D7	8F	71
9	23	29	75	8D	73	86	DE	DF	87	7A	D4	DB	28	2C	80	70
A	3C	38	64	92	62	99	C1	CE	96	65	CB	CA	37	3D	91	6F
B	C9	C3	6D	95	66	93	3F	3E	9A	67	3B	34	CC	C8	90	60
C	1C	18	44	B2	42	B9	E1	EE	B6	45	EB	EA	17	1D	B1	4F
D	E9	E3	4D	B5	46	B3	1F	1E	BA	47	1B	14	EC	E8	B0	40
E	F8	FC	52	A4	59	A2	0E	01	A5	56	0A	0B	FD	F7	AF	51
F	03	09	55	AD	53	A6	FE	FF	A7	5A	F4	FB	08	0C	A0	50

Дальше >>

Криптографические методы защиты информации

Криптографические методы защиты информации

Современные симметричные алгоритмы шифрования

7.4 Шифр "Магма" ГОСТ Р 34.12-2015

7.5 Блочный шифр Rijndael

7.5.1 Раундовое преобразование

7.5.2 Алгоритм выработки раундовых ключей

7.5.3 Дополнение. О выборе блоков замен для AES и аналогичных алгоритмов

Вопросы и ответы

Студенты

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	5C	58	04	F2	02	F9	A1	AE	F6	05	AB	AA	57	5D	F1	0F
1	A9	A3	0D	F5	06	F3	5F	5E	FA	07	5B	54	AC	A8	F0	00
2	B8	BC	12	E4	19	E2	4E	41	E5	16	4A	4B	BD	B7	EF	11
3	43	49	15	ED	13	E6	BE	BF	E7	1A	B4	BB	48	4C	E0	10
4	98	9C	32	C4	39	C2	6E	61	C5	36	6A	6B	9D	97	CF	31
5	63	69	35	CD	33	C6	9E	9F	C7	3A	94	9B	68	6C	C0	30
6	7C	78	24	D2	22	D9	81	8E	D6	25	8B	8A	77	7D	D1	2F
7	89	83	2D	D5	26	D3	7F	7E	DA	27	7B	74	8C	88	D0	20
8	D8	DC	72	84	79	82	2E	21	85	76	2A	2B	DD	D7	8F	71
9	23	29	75	8D	73	86	DE	DF	87	7A	D4	DB	28	2C	80	70
A	3C	38	64	92	62	99	C1	CE	96	65	CB	CA	37	3D	91	6F
B	C9	C3	6D	95	66	93	3F	3E	9A	67	3B	34	CC	C8	90	60
C	1C	18	44	B2	42	B9	E1	EE	B6	45	EB	EA	17	1D	B1	4F
D	E9	E3	4D	B5	46	B3	1F	1E	BA	47	1B	14	EC	E8	B0	40
E	F8	FC	52	A4	59	A2	0E	01	A5	56	0A	0B	FD	F7	AF	51
F	03	09	55	AD	53	A6	FE	FF	A7	5A	F4	FB	08	0C	A0	50

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	5C	58	04	F2	02	F9	A1	AE	F6	05	AB	AA	57	5D	F1	0F
1	A9	A3	0D	F5	06	F3	5F	5E	FA	07	5B	54	AC	A8	F0	00
2	B8	BC	12	E4	19	E2	4E	41	E5	16	4A	4B	BD	B7	EF	11
3	43	49	15	ED	13	E6	BE	BF	E7	1A	B4	BB	48	4C	E0	10
4	98	9C	32	C4	39	C2	6E	61	C5	36	6A	6B	9D	97	CF	31
5	63	69	35	CD	33	C6	9E	9F	C7	3A	94	9B	68	6C	C0	30
6	7C	78	24	D2	22	D9	81	8E	D6	25	8B	8A	77	7D	D1	2F
7	89	83	2D	D5	26	D3	7F	7E	DA	27	7B	74	8C	88	D0	20
8	D8	DC	72	84	79	82	2E	21	85	76	2A	2B	DD	D7	8F	71
9	23	29	75	8D	73	86	DE	DF	87	7A	D4	DB	28	2C	80	70
A	3C	38	64	92	62	99	C1	CE	96	65	CB	CA	37	3D	91	6F
B	C9	C3	6D	95	66	93	3F	3E	9A	67	3B	34	CC	C8	90	60
C	1C	18	44	B2	42	B9	E1	EE	B6	45	EB	EA	17	1D	B1	4F
D	E9	E3	4D	B5	46	B3	1F	1E	BA	47	1B	14	EC	E8	B0	40
E	F8	FC	52	A4	59	A2	0E	01	A5	56	0A	0B	FD	F7	AF	51
F	03	09	55	AD	53	A6	FE	FF	A7	5A	F4	FB	08	0C	A0	50

Авторизоваться

Криптографические методы защиты информации

Криптографические методы защиты информации

Современные симметричные алгоритмы шифрования

7.4 Шифр "Магма" ГОСТ Р 34.12-2015

7.5 Блочный шифр Rijndael

7.5.1 Раундовое преобразование

7.5.2 Алгоритм выработки раундовых ключей

7.5.3 Дополнение. О выборе блоков замен для AES и аналогичных алгоритмов

Вопросы и ответы

Студенты

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	5C	58	04	F2	02	F9	A1	AE	F6	05	AB	AA	57	5D	F1	0F
1	A9	A3	0D	F5	06	F3	5F	5E	FA	07	5B	54	AC	A8	F0	00
2	B8	BC	12	E4	19	E2	4E	41	E5	16	4A	4B	BD	B7	EF	11
3	43	49	15	ED	13	E6	BE	BF	E7	1A	B4	BB	48	4C	E0	10
4	98	9C	32	C4	39	C2	6E	61	C5	36	6A	6B	9D	97	CF	31
5	63	69	35	CD	33	C6	9E	9F	C7	3A	94	9B	68	6C	C0	30
6	7C	78	24	D2	22	D9	81	8E	D6	25	8B	8A	77	7D	D1	2F
7	89	83	2D	D5	26	D3	7F	7E	DA	27	7B	74	8C	88	D0	20
8	D8	DC	72	84	79	82	2E	21	85	76	2A	2B	DD	D7	8F	71
9	23	29	75	8D	73	86	DE	DF	87	7A	D4	DB	28	2C	80	70
A	3C	38	64	92	62	99	C1	CE	96	65	CB	CA	37	3D	91	6F
B	C9	C3	6D	95	66	93	3F	3E	9A	67	3B	34	CC	C8	90	60
C	1C	18	44	B2	42	B9	E1	EE	B6	45	EB	EA	17	1D	B1	4F
D	E9	E3	4D	B5	46	B3	1F	1E	BA	47	1B	14	EC	E8	B0	40
E	F8	FC	52	A4	59	A2	0E	01	A5	56	0A	0B	FD	F7	AF	51
F	03	09	55	AD	53	A6	FE	FF	A7	5A	F4	FB	08	0C	A0	50