|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Основы теории чисел
1.3 Цепные дроби
1.3.1 Представление рациональных чисел конечными цепными дробями
Пусть  ,
, 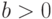 ,
,  ,
,  - целые. Число
- целые. Число  можно представить в виде дроби особого вида. Это представление получается из алгоритма Евклида. Применим алгоритм Евклида к числам
можно представить в виде дроби особого вида. Это представление получается из алгоритма Евклида. Применим алгоритм Евклида к числам  и
и  . Получим:
. Получим:
 |
( 1.5) |
Из второго равенства получаем:
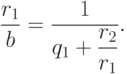 |
( 1.6) |
Подставим это выражение в первое из равенств (1.5), получим:
 |
( 1.7) |
Третье из равенств (1.5) даёт:

Подставим это выражение в (1.7), получим:

Продолжая действовать аналогично, за конечное число шагов получим:
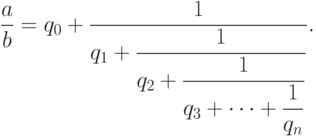 |
( 1.8) |
Определение 1.16 Дробь вида (1.8) называется конечной цепной (другое название: непрерывной) дробью.
Сокращенная (и, конечно, более удобная) запись: ![[q_0; q_1,q_2,q_3,\dots,q_n]](/sites/default/files/tex_cache/1f296845e01063347e4fc987a5dbd6b9.png) .
.
Числа 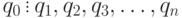 называются неполными частными, все они - целые, а начиная с
называются неполными частными, все они - целые, а начиная с  - натуральные.
- натуральные.
Равенство вида (1.8) называется представлением рационального числа конечной цепной дробью.
Теорема 1.19 Всякое рациональное число может быть представлено в виде конечной цепной дроби.
Пример 1.31
Если допустить, что последнее неполное частное может равняться 1, то для всякого рационального числа можно получить два представления в виде конечной цепной дроби.
Пример 1.32 
Теорема 1.20 Представление рационального числа в виде конечной цепной дроби, такой, что последнее неполное частное отлично от  , единственно.
, единственно.
Имеет место простая, но важная
Теорема 1.21 Всякая конечная цепная дробь есть рациональное число.
Определение 1.17 Дроби  ,
, 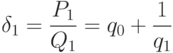 ,
,  и т.д. называются подходящими дробями цепной дроби (1.8) или соответствующего ей числа
и т.д. называются подходящими дробями цепной дроби (1.8) или соответствующего ей числа  .
.
Очевидно, что последняя подходящая дробь  есть число
есть число  . Каждая подходящая дробь есть некоторое рациональное число. Заметим, что
. Каждая подходящая дробь есть некоторое рациональное число. Заметим, что  -я подходящая дробь
-я подходящая дробь  получается заменой
получается заменой  на
на  .
.
Подходящие дроби последовательно можно представить в виде:


Общая формула имеет вид:
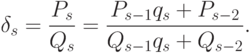
Напомним кратко основные свойства цепных дробей.
- Числители и знаменатели подходящих дробей - целые числа, знаменатели, кроме того, числа натуральные и образуют возрастающую последовательность.
- Числители и знаменатели двух соседних подходящих дробей связаны соотношением:
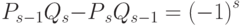 .
. - Подходящие дроби несократимы, т.е.
 .
.

![\dfrac{37}{15}=2+\dfrac{1}{2+\dfrac{1}{7}}=[2;2,7]](/sites/default/files/tex_cache/5428c1b7e38a95e6567ab685c22adc49.png)
![\dfrac{13}{141}=0+\dfrac{1}{10+\dfrac{1}{1+\dfrac{1}{5+\dfrac{1}{2}}}}=[0;10,1,5,2]](/sites/default/files/tex_cache/f65c68502e4907118c530cf821ed576b.png)
![\dfrac{-43}{15}=-2\dfrac{13}{15}=-3+\dfrac{2}{15}=-3+\dfrac{1}{7+\dfrac{1}{2}}=[-3;7,2]](/sites/default/files/tex_cache/b1c293ece4f3ddd41d5361ab8854e625.png)
![\dfrac{-23}{29}=-1\dfrac{6}{29}=-1+\dfrac{1}{4+\dfrac{1}{1+\dfrac{1}{5}}}=[-1;4,1,5]](/sites/default/files/tex_cache/dee70ee79ab08cac1e89adefbc945a3d.png)
![\dfrac{1}{17}=[0;17]](/sites/default/files/tex_cache/ecfc4dfd2cde2349a8cc742fda0ab518.png)
![5=[5]](/sites/default/files/tex_cache/b01c3d13abae3e4eaa4fa6faa6c10f93.png)
![-13=[-13]](/sites/default/files/tex_cache/7bf0c25edec80639d079ee7ae062df9d.png)