Параллельные методы на графах

10.3. Задача оптимального разделения графов

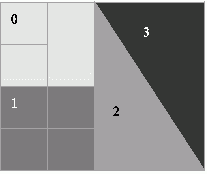
Проблема оптимального разделения графов относится к числу часто возникающих задач при проведении различных научных исследований, использующих параллельные вычисления. В качестве примера можно привести задачи обработки данных, в которых области расчетов аппроксимируются двумерными или трехмерными вычислительными сетками. Получение результатов в таких задачах сводится, как правило, к выполнению тех или иных процедур обработки для каждого элемента (узла) сети. При этом в ходе вычислений между соседними элементами сети может происходить передача результатов обработки и т.п. Эффективное решение таких задач на многопроцессорных системах с распределенной памятью предполагает разделение сети между процессорами таким образом, чтобы каждому из процессоров выделялось примерно равное число элементов сети, а межпроцессорные коммуникации, необходимые для выполнения информационного обмена между соседними элементами, были минимальными. На рис. 10.9 показан пример нерегулярной сети, разделенной на 4 части (различные части разбиения сети выделены темным цветом различной интенсивности).

Рис. 10.9. Пример разделения нерегулярной сети

Очевидно, что такие задачи разделения сети между процессорами могут быть сведены к проблеме оптимального разделения графа. Данный подход целесообразен, потому что представление модели вычислений в виде графа позволяет легче решить вопросы хранения обрабатываемых данных и предоставляет возможность применения типовых алгоритмов обработки графов.

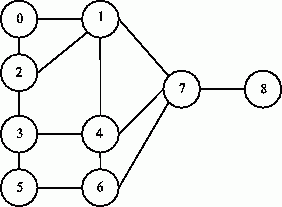
Для представления сети в виде графа каждому элементу сети можно поставить в соответствие вершину графа, а дуги графа использовать для отражения свойства близости элементов сети (например, определять дуги между вершинами графа тогда и только тогда, когда соответствующие элементы исходной сети являются соседними). При таком подходе, например, для сети на рис. 10.9, будет сформирован граф, приведенный на рис. 10.10.

Рис. 10.10. Пример графа, моделирующего структуру сети на рис. 10.9

Дополнительная информация по проблеме разделения графов может быть получена, например, в [ [ 67 ] ].

Задача оптимального разделения графов сама может являться предметом распараллеливания. Это бывает необходимо в тех случаях, когда вычислительной мощности и объема оперативной памяти обычных компьютеров недостаточно для эффективного решения задачи. Параллельные алгоритмы разделения графов рассматриваются во многих научных работах: [ [ 20 ] , [ 38 ] , [ 44 ] , [ 48 ] , [ 49 ] , [ 65 ] , [ 74 ] ].

10.3.1. Постановка задачи оптимального разделения графов

Пусть дан взвешенный неориентированный граф G=(V,E), каждой вершине 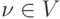и каждому ребру 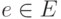которого приписан вес. Задача оптимального разделения графа состоит в разбиении его вершин на непересекающиеся подмножества с максимально близкими суммарными весами вершин и минимальным суммарным весом ребер, проходящих между полученными подмножествами вершин.

Следует отметить возможную противоречивость указанных критериев разбиения графа – равновесность подмножеств вершин может не соответствовать минимальности весов граничных ребер и наоборот. В большинстве случаев необходимым является выбор того или иного компромиссного решения. Так, в случае невысокой доли коммуникаций может оказаться эффективной оптимизация веса ребер только среди решений, обеспечивающих оптимальное разбиение множества вершин по весу.

Далее для простоты изложения учебного материала будем полагать веса вершин и ребер графа равными единице.

10.3.2. Метод рекурсивного деления пополам

Для решения задачи разбиения графа можно рекурсивно применить метод бинарного деления ( the binary bisection method ), при котором на первой итерации граф разделяется на две равные части, далее на втором шаге каждая из полученных частей также разбивается на две части и т. д. В данном подходе для разбиения графа на k частей необходимо log₂k уровней рекурсии и выполнение k-1 деления пополам. В случае когда требуемое количество разбиений k не является степенью двойки, каждое деление пополам необходимо осуществлять в соответствующем соотношении.

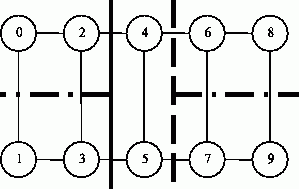
Поясним схему работы метода деления пополам на примере разделения графа на рис. 10.11 на 5 частей. Сначала граф следует разделить на 2 части в оотношении 2:3 (непрерывная линия), затем правую часть разбиения – в отношении 1:3 (штриховая линия), после этого осталось разделить 2 крайние подобласти слева и справа в отношении 1:1 (штрих-пунктир).

Рис. 10.11. Пример разбиения графа на 5 частей методом рекурсивного деления пополам

10.3.3. Геометрические методы

Геометрические методы (см., например, [ [ 21 ] , [ 35 ] , [ 44 ] , [ 53 ] , [ 55 ] , [ 58 ] , [ 61 ] , [ 65 ] ]) выполняют разбиение сетей, основываясь исключительно на координатной информации об узлах сети. Так как эти методы не принимают во внимание информацию о связности элементов сети, они не могут явно привести к минимизации суммарного веса граничных ребер (в терминах графа, соответствующего сети). Для минимизации межпроцессорных коммуникаций геометрические методы оптимизируют некоторые вспомогательные показатели (например, длину границы между разделенными участками сети).

Обычно геометрические методы не требуют большого объема вычислений, однако качество их разбиения уступает методам, принимающим во внимание связность элементов сети.

10.3.3.1. Покоординатное разбиение

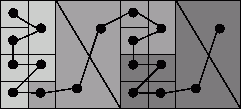
Покоординатное разбиение ( the coordinate nested dissection ) – это метод, основанный на рекурсивном делении пополам сети по наиболее длинной стороне. В качестве иллюстрации на рис. 10.12 показан пример сети, при разделении которой именно такой способ разбиения дает существенно меньшее количество информационных связей между разделенными частями, по сравнению со случаем, когда сеть делится по меньшей (вертикальной) стороне.

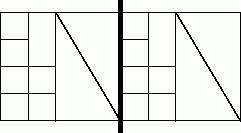
Рис. 10.12. Пример разделения сети графическим методом по наибольшей размерности (граница раздела показана жирной линией)

Общая схема выполнения метода состоит в следующем. Сначала вычисляются центры масс элементов сети. Полученные точки проектируются на ось, соответствующую наибольшей стороне разделяемой сети. Таким образом мы получаем упорядоченный список всех элементов сети. Делением списка пополам (возможно, в нужной пропорции) мы получаем требуемую бисекцию. Аналогичным способом полученные фрагменты разбиения рекурсивно делятся на нужное число частей.

Метод координатного вложенного разбиения работает очень быстро и требует небольшого количества оперативной памяти. Однако получаемое разбиение уступает по качеству более сложным и вычислительно трудоемким методам. Кроме того, в случае сложной структуры сети алгоритм может получать разбиение с несвязанными подсетями.

10.3.3.2. Рекурсивный инерционный метод деления пополам

Предыдущая схема могла производить разбиение сети только по линии, перпендикулярной одной из координатных осей. Во многих случаях такое ограничение оказывается критичным для построения качественного разбиения. Достаточно повернуть сеть на рис. 10.12 под острым углом к координатным осям (см. рис. 10.13), чтобы убедиться в этом. Для минимизации границы между подсетями желательна возможность проведения линии разделения с любым требуемым углом поворота. Возможный способ определения угла поворота, используемый в рекурсивном инерционном методе деления пополам ( the recursive inertial bisection ), состоит в использовании главной инерционной оси (см., например, [ [ 62 ] ]), считая элементы сети точечными массами. Линия бисекции, ортогональная полученной оси, как правило, дает границу наименьшей длины.

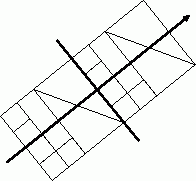
Рис. 10.13. Пример разделения сети методом рекурсивной инерционной бисекции. Стрелкой показана главная инерционная ось

10.3.3.3. Деление сети с использованием кривых Пеано

Одним из недостатков предыдущих графических методов является то, что при каждой бисекции эти методы учитывают только одну размерность. Таким образом, схемы, учитывающие больше размерностей, могут обеспечить лучшее разбиение.

Один из таких методов упорядочивает элементы в соответствии с позициями центров их масс вдоль кривых Пеано. Кривые Пеано – это кривые, полностью заполняющие области больших размерностей (например, квадрат или куб). Применение таких кривых обеспечивает близость точек фигуры, которые соответствуют точкам, близким на кривой. После получения списка элементов сети, упорядоченного в зависимости от расположения на кривой, достаточно разделить список на необходимое число частей в соответствии с установленным порядком. Получаемый в результате такого подхода метод носит в литературе наименование алгоритма деления сети с использованием кривых Пеано ( the space-filling curve technique ). Подробнее о методе можно прочитать в работах [ [ 56 ] , [ 58 ] , [ 61 ] ].

Рис. 10.14. Пример разделения сети на 3 части с использованием кривых Пеано