|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Экономико-математические модели и принятие решений
Средние издержки (на единицу времени) таковы:

Итак, минимизация средних издержек - это задача дискретной оптимизации. На третьем этапе построения оптимального плана необходимо найти натуральное число 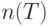 - самое выгодное число поставок.
- самое выгодное число поставок.
Поскольку к моменту  запас товара должен быть израсходован, то общий объем поставок за время
запас товара должен быть израсходован, то общий объем поставок за время  должен совпадать с общим объемом спроса, следовательно, равняться
должен совпадать с общим объемом спроса, следовательно, равняться 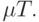 Справедливо балансовое соотношение (аналог закона Ломоносова-Лавуазье сохранения массы при химических реакциях):
Справедливо балансовое соотношение (аналог закона Ломоносова-Лавуазье сохранения массы при химических реакциях):
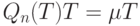
Из балансового соотношения следует, что
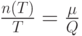
Средние издержки (на единицу времени) можно выразить как функцию размера партии  :
:
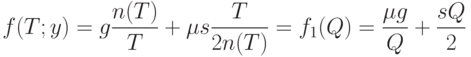 |
( 33) |
Задача состоит в минимизации  по
по  . При этом возможная величина поставки принимает дискретные значения,
. При этом возможная величина поставки принимает дискретные значения, 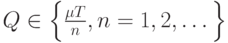
Изучим функцию  , определенную при
, определенную при 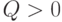 . При приближении к 0 она ведет себя как гипербола, при росте аргумента - как линейная функция. Производная имеет вид
. При приближении к 0 она ведет себя как гипербола, при росте аргумента - как линейная функция. Производная имеет вид
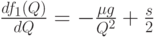
Производная монотонно возрастает, поэтому рассматриваемая функция имеет единственный минимум в точке, в которой производная равна 0, т.е. при
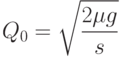 |
( 34) |
Получена знаменитая "формула квадратного корня".
В литературе иногда без всяких комментариев рекомендуют использовать напряженный план, в котором размеры всех поставляемых партий равны 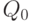 . К сожалению, получаемый таким путем план почти всегда не является оптимальным, т.е. популярная рекомендация неверна или не вполне корректна. Дело в том, что почти всегда
. К сожалению, получаемый таким путем план почти всегда не является оптимальным, т.е. популярная рекомендация неверна или не вполне корректна. Дело в том, что почти всегда
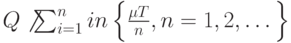
Всегда можно указать неотрицательное целое число  такое, что
такое, что
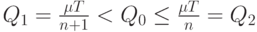 |
( 35) |
Утверждение 3. Решением задачи оптимизации
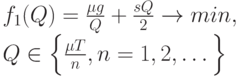
является либо 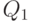 , либо
, либо 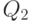 .
.
Действительно, из всех 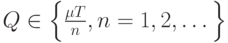 часть лежит правее
часть лежит правее 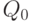 , из них наименьшим является
, из них наименьшим является 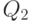 , а часть лежит левее
, а часть лежит левее 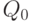 , из них наибольшим является
, из них наибольшим является 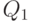 . Для построения оптимального плана обратим внимание на то, что производная функции
. Для построения оптимального плана обратим внимание на то, что производная функции  отрицательна левее
отрицательна левее 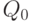 и положительна правее
и положительна правее 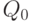 , следовательно, функция средних издержек
, следовательно, функция средних издержек  убывает левее
убывает левее 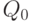 и возрастает правее
и возрастает правее 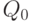 . Значит, минимум по
. Значит, минимум по 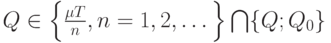 достигается при
достигается при  , а минимум по
, а минимум по 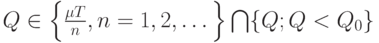 - при
- при  Последнее утверждение эквивалентно заключению утверждения 3.
Последнее утверждение эквивалентно заключению утверждения 3.
Итак, алгоритм построения оптимального плана таков.
- Найти
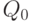 по формуле квадратного корня (34).
по формуле квадратного корня (34). - Найти n из условия (35).
- Рассчитать
 ) по формуле (33) для
) по формуле (33) для  и
и  , где
, где 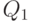 и
и 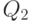 определены в (35).
определены в (35). - Наименьшее из двух чисел
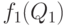 и
и 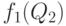 является искомым минимумом, а то из чисел
является искомым минимумом, а то из чисел 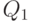 и
и 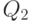 , на котором достигается минимум - решением задачи оптимизации. Обозначим его
, на котором достигается минимум - решением задачи оптимизации. Обозначим его 
Оптимальный план поставки - это напряженный план, в котором объемы всех поставок равны  .
.
Замечание. Если 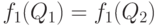 , то решение задачи оптимизации состоит из двух точек
, то решение задачи оптимизации состоит из двух точек 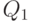 и
и 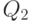 . В этом частном случае существует два оптимальных плана.
. В этом частном случае существует два оптимальных плана.
Пример 1. На складе хранится некоторая продукция, пользующаяся равномерным спросом. За 1 день со склада извлекается 5 т продукции. Плата за хранение 1 т продукции в день - 50 руб. Плата на доставку одной партии - 980 руб. Горизонт планирования - 10 дней. Найти оптимальный план поставок.
В рассматриваемом случае 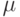 =5 (т/день),
=5 (т/день),  =50 (руб./т.день),
=50 (руб./т.день), 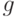 =980 (руб./партия),
=980 (руб./партия),  = 10 (дней). По формуле (34) рассчитываем
= 10 (дней). По формуле (34) рассчитываем
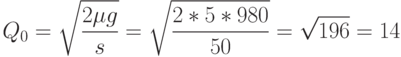
Множество допустимых значений для 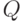 имеет вид
имеет вид
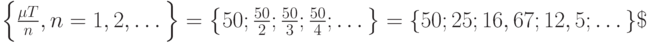
Следовательно, 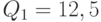 и
и 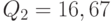 . Первое значение определяет напряженный план с четырьмя одинаковыми зубцами, а второе - с тремя. Поскольку
. Первое значение определяет напряженный план с четырьмя одинаковыми зубцами, а второе - с тремя. Поскольку
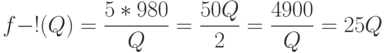
то
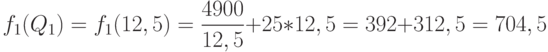
и
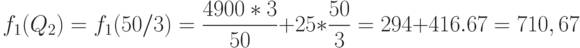
Поскольку 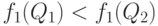 , то
, то  . Итак, оптимальным является напряженный план с четырьмя зубцами.
. Итак, оптимальным является напряженный план с четырьмя зубцами.
Как уже отмечалось, часто рекомендуют применять план поставок с  . Каков при этом проигрыш по сравнению с оптимальным планом?
. Каков при этом проигрыш по сравнению с оптимальным планом?
Для плана с  интервал между поставками составляет
интервал между поставками составляет 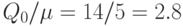 дня. Следовательно, партии придут в моменты
дня. Следовательно, партии придут в моменты 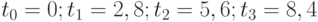 . Следующая партия должна была бы придти уже за пределами горизонта планирования
. Следующая партия должна была бы придти уже за пределами горизонта планирования 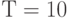 , в момент
, в момент 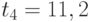 . Таким образом, график уровня запаса на складе в пределах горизонта планирования состоит из трех полных зубцов и одного не полного. К моменту
. Таким образом, график уровня запаса на складе в пределах горизонта планирования состоит из трех полных зубцов и одного не полного. К моменту 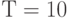 пройдет
пройдет 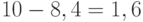 дня с момента последней поставки, значит, со склада будет извлечено
дня с момента последней поставки, значит, со склада будет извлечено 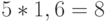 т продукции и останется
т продукции и останется 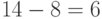 т. План с
т. План с  не является напряженным, а потому не является оптимальным для горизонта планирования
не является напряженным, а потому не является оптимальным для горизонта планирования 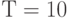 .
.
Подсчитаем общие издержки в плане с  . Площадь под графиком уровня запаса на складе равна сумме площадей трех треугольников и трапеции. Площадь треугольника равна
. Площадь под графиком уровня запаса на складе равна сумме площадей трех треугольников и трапеции. Площадь треугольника равна 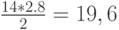 трех треугольников - 58,8. Основания трапеции параллельны оси ординат и равны значениям уровня запаса в моменты времени
трех треугольников - 58,8. Основания трапеции параллельны оси ординат и равны значениям уровня запаса в моменты времени 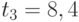 и
и 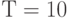 , т.е. величинам 14 и 6 соответственно. Высота трапеции лежит на оси абсцисс и равна
, т.е. величинам 14 и 6 соответственно. Высота трапеции лежит на оси абсцисс и равна 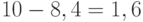 , а потому площадь трапеции есть
, а потому площадь трапеции есть 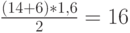 Следовательно, площадь под графиком равна
Следовательно, площадь под графиком равна  , а плата за хранение составляет
, а плата за хранение составляет 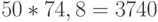 руб.
руб.
За 10 дней доставлены 4 партии товара (в моменты 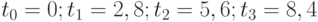 ), следовательно, затраты на доставку равны
), следовательно, затраты на доставку равны 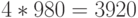 руб. Общие издержки за 10 дней составляют
руб. Общие издержки за 10 дней составляют 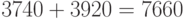 руб., а средние издержки - 766 руб. Они больше средних издержек в оптимальном плане в
руб., а средние издержки - 766 руб. Они больше средних издержек в оптимальном плане в 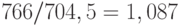 раза, т.е. на 8,7%.
раза, т.е. на 8,7%.
Отметим, что
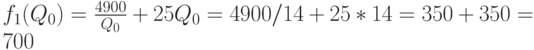
т.е. меньше, чем в оптимальном плане. Таким образом, из-за дискретности множества допустимых значений средние издержки возросли на 4,5 руб., т.e. на 0,64%. При этом оптимальный размер партии (12,5 т) отличается от 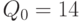 т на 1,5 т, т.е.
т на 1,5 т, т.е. 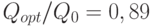 - различие на 11%. Достаточно большое различие объемов поставок привело к пренебрежимо малому изменению функции
- различие на 11%. Достаточно большое различие объемов поставок привело к пренебрежимо малому изменению функции  . Это объясняется тем, что в точке
. Это объясняется тем, что в точке 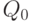 функция
функция  достигает минимума, а потому ее производная в этой точке равна 0.
достигает минимума, а потому ее производная в этой точке равна 0.
Оба слагаемых в 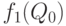 равны между собой. Случайно ли это? Покажем, что нет. Действительно,
равны между собой. Случайно ли это? Покажем, что нет. Действительно,
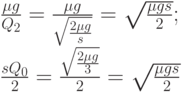
образом, составляющие средних издержек, порожденные различными причинами, уравниваются между собой.
Средние издержки в плане с  равны
равны  . Интервал между поставками при этом равен
. Интервал между поставками при этом равен
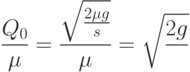
Издержки в течение одного интервала между поставками таковы:
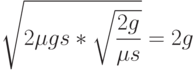
при этом половина (т.е. 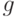 ) приходится на оплату доставки партии, а половина - на хранение товара.
) приходится на оплату доставки партии, а половина - на хранение товара.
