Системы компьютерной алгебры
Создание графических изображений
В системе Mathematica для построения графиков вида y=f(x) используется функция Plot, первым параметром которой является функция или список функций, графики которых должны быть построены, а вторым - список из трех величин: аргумент функций и концы промежутка, на котором должен быть построен график, например,
Plot[{Sin[x/2], 1.5 Sin[2x]}, {x, -3Pi,3Pi}]
Полученные изображения можно сохранить в форматах EPS, GIF, PDF, TIFF и некоторых других (смотри Help) при помощи функции Display. Ее первым аргументом является имя создаваемого файла, заключенное в кавычки, вторым - графическое изображение, а третьим - формат выходного файла, например,
Display["g1.gif",
Plot[ArcTan[x]-0.5, {x, -10, 10}],
"GIF"]Для каждого графика можно задать набор параметров PlotStyle, задающий цвет, толщину и тип линии графика. Опция RGBColor[r,g,b] (каждая составляющая есть число в диапазоне от 0 до 1) задает цвет графика в цветовой модели RGB. Для применения цветовой модели HSB (H - hue, тон; S - saturation, насыщенность; B - brightness, яркость) указывается опция Hue[h, s, b], (h, s и b из интервала [0; 1]). Возможно указание сокращенной формы этой опции - Hue[h], соответствующей значению Hue[h, 1, 1]. В следующем примере используются две различные цветовые модели для изображения двух графиков:
Plot[{Sin[x], Sin[2x]}, {x, -2Pi,2Pi},
PlotStyle -> {RGBColor[1,0,0], Hue[.4]}]Другими опциями PlotStyle являются толщина линии (Thickness) и характеристики пунктирной линии (Dashing):
Plot[{x Sin[2x], x^3 - 3x +1}, {x, -4, 4},
PlotStyle -> {{Hue[0], Thickness[.01]},
{Hue[.6], Dashing[{.02}]}}]Функция Plot допускает задание множества других опций, относящихся как ко всему изображению в целом, так и к каждому из его составляющих в отдельности. Их полный список можно получить при помощи команды Options[Plot]. Вот примеры использования некоторых из них:
| Frame -> True | Заключает рисунок в рамку |
| PlotRange -> {-5, 5} | Задает диапазон по оси OY |
| Ticks -> {{-Pi, 0, Pi}, Automatic} | Задает отметки на оси OX |
| PlotLabel -> "Sin[x]/x" | Задает заголовок рисунка |
Пример
На следующем рисунке изображен график функции arctg x и две его горизонтальные ассимптоты (PI/2 и -PI/2). Опция PlotStyle задает параметры каждого графика в отдельности, а остальные опции задают внешний вид всего изображения в целом. Переменная p2 используется затем для сохранения изображения.
p2=Plot[{ArcTan[x], Pi/2, - Pi/2}, {x, -10, 10},
PlotStyle -> {{RGBColor[0, 1, 0]},
{RGBColor[1, 0, 1], Dashing[{.015}]},
{RGBColor[1, 0, 1], Dashing[{.015}]}},
Ticks -> {Automatic, {-Pi/2, -Pi/4, Pi/4, Pi/2}},
PlotLabel->"f(x) = arctg(x)",
PlotRange ->{-2, 2}]Для сохранения в файле g2.gif полученного изображения в формате GIF использовалась функция Display:
Display["g2.gif", p2, "GIF"]
Функция ParametricPlot используется для рисования графиков функций, заданных параметрически. Отметим, что Mathematica по умолчанию отображает графические объекты таким образом, что отношение высоты рисунка к его ширине равно величине, обратной золотому сечению (около 0.618034). Для сохранения естественных пропорций изображения следует указывать опцию AspectRatio -> Automatic. После этого круг выглядит действительно кругом, а не овалом. Ниже приведены примеры, демонстрирующие построение параметрически заданных кривых.
ParametricPlot[{Sin[t], Cos[t]}, {t, 0, 2Pi}]
ParametricPlot[{Sin[t], Cos[t]},
{t, 0, 2Pi}, AspectRatio -> Automatic]
ParametricPlot[{Sin[3t], Cos[2t]},
{t, 2Pi/3, 4Pi/3}, AspectRatio -> Automatic]
ParametricPlot[{{Sin[2t], Sin[3t]},
{0.5*Sin[t], 0.5*Cos[t]}},
{t, 0, 2Pi}, AspectRatio -> Automatic]Для построения графиков в полярной системе координат следует предварительно загрузить модуль расширения Graphics, после чего использовать функцию PolarPlot:
<<Graphics`Graphics`
PolarPlot[phi, {phi,0,10Pi}]
PolarPlot[Cos[t], {t,0,2 Pi}]
PolarPlot[Cos[a]^2 -Sin[a]^2,{a,0,2Pi}]
PolarPlot[Sin[5t],{t,0,2 Pi}]
PolarPlot[1-Sin[fi],{fi,0,2Pi}]Функции Plot3D и ParametricPlot3D являются основными инструментами программы Mathematica для изображения трехмерных графических объектов. Эти функции кроме трех обязательных параметров, задающих функцию и диапазоны изменения переменных, используют множество дополнительных опций. Отметим среди них только PlotPoints, указывающую на сколько частей следует разбить интервалы изменения переменных. Ниже приведены два примера использования этих функций.
Plot3D[Sin[xy],
{x, 0, 4}, {y, 0, 4},
PlotPoints -> 40,
Mesh ->False,
FaceGrids ->All,
AxesLabel ->
{"Length", "Width", "Height"}] |
|
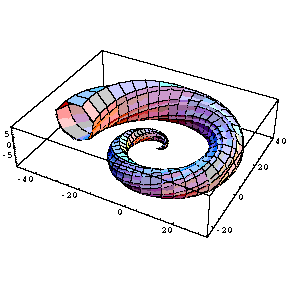
ParametricPlot3D[
{u Cos[u](4 + Cos[u+v]),
u Sin[u](4 + Cos[u+v]),
u Sin[u + v]},
{u, 0, 3Pi},{v, 0, 3Pi},
PlotPoints ->{60, 12}] |
Следующие изображения построены при помощи модуля расширения Graphics
Построение икосаэдра<<Graphics`Polyhedra`
Show[Polyhedron[Icosahedron],
Boxed -> False] |
|
Лист Мебиуса - пример односторонней поверхности<<Graphics`Shapes` Show[Graphics3D[ MoebiusStrip[2, 0.5, 150], Boxed ->False]] |
|
Сфера с отверстием<<Graphics`ContourPlot3D`
ContourPlot3D[
Cos[Sqrt[x^2+y^2+z^2]],
{x, -2, 2},
{y, -1.5, 2},
{z, -2, 2},
Boxed -> False,
PlotPoints ->{3,15}] |
Задания
Постройте графики следующих функций, используя различные параметры, задающие цвет и тип линий, добавьте подписи к рисункам и сохраните их в формате GIF: