|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Временная стоимость денег
2.1 Основы финансовых вычислений
Одним из важнейших свойств денежных потоков является их распределенность во времени. При анализе относительно краткосрочных периодов (до 1 года) в условиях стабильной экономики данное свойство оказывает относительно незначительное влияние, которым часто пренебрегают. Определяя годовой объем реализации по предприятию, просто складывают суммы выручки за каждый из месяцев отчетного года. Аналогично поступают со всеми остальными денежными потоками, что позволяет оперировать их итоговыми значениями. Однако в случае более длительных периодов или в условиях сильной инфляции возникает серьезная проблема обеспечения сопоставимости данных. Одна и та же номинальная сумма денег, полученная предприятием с интервалом в 1 и более год, в таких условиях будет иметь для него неодинаковую ценность. Очевидно, что 1 млн. рублей в начале 1992 года был значительно весомее миллиона "образца" 1993 и более поздних лет. Как правило, в таких случаях производят корректировку отчетных данных с учетом инфляции. Но проблема не сводится только к учету инфляции. Одним из основополагающих принципов финансового менеджмента является признание временной ценности денег, то есть зависимости их реальной стоимости от величины промежутка времени, остающегося до их получения или расходования. В экономической теории данное свойство называется положительным временным предпочтением.
Наряду с инфляционным обесцениванием денег существует еще как минимум три важнейшие причины данного экономического феномена. Во-первых, "сегодняшние" деньги всегда будут ценнее "завтрашних" из-за риска неполучения последних, и этот риск будет тем выше, чем больше промежуток времени, отделяющий получателя денег от этого "завтра". Во-вторых, располагая денежными средствами "сегодня", экономический субъект может вложить их в какое-нибудь доходное предприятие и заработать прибыль, в то время как получатель будущих денег лишен этой возможности. Расставаясь с деньгами "сегодня" на определенный период времени (допустим, давая их взаймы на 1 месяц), владелец не только подвергает себя риску их невозврата, но и несет реальные экономические потери в форме неполученных доходов от инвестирования. Кроме того снижается его платежеспособность, так как любые обязательства, получаемые им взамен денег, имеют более низкую ликвидность, чем "живые" деньги. То есть у кредитора возрастает риск потери ликвидности, и это третья причина положительного временного предпочтения. Естественно, большинство владельцев денег не согласны бесплатно принимать на себя столь существенные дополнительные риски. Поэтому, предоствляя кредит, они устанавливают такие условия его возврата, которые по их мнению полностью возместят им все моральные и материальные неудобства, возникающие у человека, расстающегося (пусть даже и временно) с денежными знаками.
Количественной мерой величины этого возмещения является процентная ставка. С ее помощью может быть определена как будущая стоимость "сегодняшних" денег (например, если их собираются ссудить), так и настоящая (современная, текущая или приведенная) стоимость "завтрашних" денег – например, тех, которыми обещают расплатиться через год после поставки товаров или оказания услуг. В первом случае говорят об операции наращения, поэтому будущую стоимость денег часто называют наращенной. Во втором случае выполняется дисконтирование или приведение будущей стоимости к ее современной величине (текущему моменту) – отсюда термин дисконтированная, приведенная или текущая стоимость. Операции наращения денег по процентной ставке более просты и понятны, так как с ними приходится сталкиваться довольно часто беря или давая деньги взаймы. Однако для финансового менеджмента значительно более важное значение имеет дисконтирование денежных потоков, приведение их будущей стоимости к современному моменту времени для обеспечения сопоставимости величины распределенных по времени платежей. В принципе, дисконтирование – это наращение "наоборот", однако для финансовых расчетов важны детали, поэтому необходимо более подробно рассмотреть как прямую, так и обратную задачу процентных вычислений. Прежде чем рассматривать их применительно к денежным потокам, следует усвоить наиболее элементарные операции с единичными суммами (разовыми платежами).
Процентная ставка показывает степень интенсивности изменения стоимости денег во времени. Абсолютная величина этого изменения называется процентом, измеряется в денежных единицах (например, рублях) и обозначается  . Если обозначить будущую сумму
. Если обозначить будущую сумму  , а современную (или первоначальную)
, а современную (или первоначальную)  , то
, то 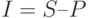 . Процентная ставка
. Процентная ставка  является относительной величиной, измеряется в десятичных дробях или
является относительной величиной, измеряется в десятичных дробях или  , и определяется делением процентов на первоначальную сумму:
, и определяется делением процентов на первоначальную сумму:
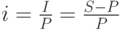 |
( 1) |
Можно заметить, что формула расчета процентной ставки идентична расчету статистического показателя "темп прироста". Действительно, если абсолютная сумма процента (  ) представляет собой прирост современной величины, то отношение этого прироста к самой современной величине и будет темпом прироста первоначальной суммы. Наращение первоначальной суммы по процентной ставке называется декурсивным методом начисления процентов.
) представляет собой прирост современной величины, то отношение этого прироста к самой современной величине и будет темпом прироста первоначальной суммы. Наращение первоначальной суммы по процентной ставке называется декурсивным методом начисления процентов.
Кроме процентной существует учетная ставка  (другое название – ставка дисконта), величина которой определяется по формуле:
(другое название – ставка дисконта), величина которой определяется по формуле:
 |
( 2) |
где  – сумма дисконта.
– сумма дисконта.
Сравнивая формулы (1) и (2) можно заметить, что сумма процентов  и величина дисконта
и величина дисконта  определяются одинаковым образом – как разница между будущей и современной стоимостями. Однако, смысл, вкладываемый в эти термины неодинаков. Если в первом случае речь идет о приросте текущей стоимости, своего рода "наценке", то во втором определяется снижение будущей стоимости, "скидка" с ее величины. (Diskont в переводе с немецкого означает "скидка"). Неудивительно, что основной областью применения учетной ставки является дисконтирование, процесс, обратный по отношению к начислению процентов. Тем не менее, иногда она используется и для наращения. В этом случае говорят об антисипативных процентах.
определяются одинаковым образом – как разница между будущей и современной стоимостями. Однако, смысл, вкладываемый в эти термины неодинаков. Если в первом случае речь идет о приросте текущей стоимости, своего рода "наценке", то во втором определяется снижение будущей стоимости, "скидка" с ее величины. (Diskont в переводе с немецкого означает "скидка"). Неудивительно, что основной областью применения учетной ставки является дисконтирование, процесс, обратный по отношению к начислению процентов. Тем не менее, иногда она используется и для наращения. В этом случае говорят об антисипативных процентах.
При помощи рассмотренных выше ставок могут начисляться как простые так и сложные проценты. При начислении простых процентов наращение первоначальной суммы происходит в арифметической прогрессии, а при начислении сложных процентов – в геометрической. Вначале более подробно рассмотрим операции с простыми процентами.
Начисление простых декурсивных и антисипативных процентов производится по различным формулам:
декурсивные проценты:
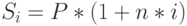 |
( 3) |
антисипативные проценты:
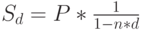 |
( 4) |
где  – продолжительность ссуды, измеренная в годах.
– продолжительность ссуды, измеренная в годах.
Для упрощения вычислений вторые сомножители в формулах (3) и (4) называются множителями наращения простых процентов: 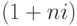 – множитель наращения декурсивных процентов ;
– множитель наращения декурсивных процентов ; 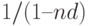 – множитель наращения антисипативных процентов.
– множитель наращения антисипативных процентов.
Например, ссуда в размере 1 млн. рублей выдается сроком на 0,5 года под 30% годовых. В случае декурсивных процентов наращенная сумма ( 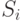 ) будет равна 1,15 млн. рублей (1 * (1 + 0,5 * 0,3), а сумма начисленных процентов (
) будет равна 1,15 млн. рублей (1 * (1 + 0,5 * 0,3), а сумма начисленных процентов (  ) – 0,15 млн. рублей (1,15 – 1). Если же начислять проценты по антисипативному методу, то наращенная величина (
) – 0,15 млн. рублей (1,15 – 1). Если же начислять проценты по антисипативному методу, то наращенная величина ( 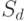 ) составит 1,176 млн. рублей (1 * (1 / (1 – 0,5 * 0,3), а сумма процентов (
) составит 1,176 млн. рублей (1 * (1 / (1 – 0,5 * 0,3), а сумма процентов (  ) 0,176 млн. рублей. Наращение по антисипативному методу всегда происходит более быстрыми темпами, чем при использовании процентной ставки. Поэтому банки используют этот метод для начисления процентов по выдаваемым ими ссудам в периоды высокой инфляции. Однако у него есть существенный недостаток: как видно из формулы (4), при
) 0,176 млн. рублей. Наращение по антисипативному методу всегда происходит более быстрыми темпами, чем при использовании процентной ставки. Поэтому банки используют этот метод для начисления процентов по выдаваемым ими ссудам в периоды высокой инфляции. Однако у него есть существенный недостаток: как видно из формулы (4), при 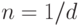 , знаменатель дроби обращается в нуль и выражение теряет
смысл.
, знаменатель дроби обращается в нуль и выражение теряет
смысл.
Вообще, начисление процентов с использованием ставки, предназначенной для выполнения прямо противоположной операции – дисконтирования – имеет оттенок некой "неестественности" и иногда порождает неразбериху (аналогичную той, которая может возникнуть у розничного торговца, если он перепутает правила определения скидок и наценок на свои товары). С позиции математики никакой сложности здесь нет, преобразовав (1), (2) и (4), получаем:
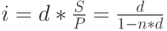 |
( 5) |
Соблюдая это условие, можно получать эквивалентные результаты, начисляя проценты как по формуле (3), так и по формуле (4).
Антисипативным методом начисления процентов обычно пользуются в чисто технических целях, в частности, для определения суммы, дисконтирование которой по заданным учетной ставке и сроку, даст искомый результат. В следующем параграфе будут рассмотрены конкретные примеры возникновения подобных ситуаций.
Как правило, процентные ставки устанавливаются в годовом исчислении, поэтому они называются годовыми. Особенностью простых процентов является то, что частота процессов наращения в течение года не влияет на результат. То есть нет никакой разницы начислять 30% годовых 1 раз в год или начислить 2 раза по 15% годовых. Простая ставка 30% годовых при одном начислении в году называется эквивалентной простой ставке 15% годовых при начислении 1 раз в полгода. Данное свойство объясняется тем, что процесс наращения по простой процентной ставке представляет собой арифметическую прогрессию с первым членом  и разностью
и разностью 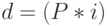 .
.
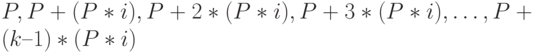
Наращенная сумма  есть ничто иное как последний k-й член этой прогрессии (
есть ничто иное как последний k-й член этой прогрессии ( 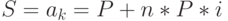 ), срок ссуды
), срок ссуды  равен
равен 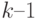 . Поэтому, если увеличить
. Поэтому, если увеличить  и одновременно пропорционально уменьшить
и одновременно пропорционально уменьшить  , то величина каждого члена прогрессии, в том числе и последнего, останется неизменной.
, то величина каждого члена прогрессии, в том числе и последнего, останется неизменной.
Однако продолжительность ссуды (или другой финансовой операции, связанной с начислением процентов)  необязательно должна равняться году или целому числу лет. Напротив, простые проценты чаще всего используются при краткосрочных (длительностью менее года) операциях. В этом случае возникает проблема определения длительности ссуды и продолжительности года в днях. Если обозначить продолжительность года в днях буквой
необязательно должна равняться году или целому числу лет. Напротив, простые проценты чаще всего используются при краткосрочных (длительностью менее года) операциях. В этом случае возникает проблема определения длительности ссуды и продолжительности года в днях. Если обозначить продолжительность года в днях буквой  (этот показатель называется временная база), а количество дней пользования ссудой
(этот показатель называется временная база), а количество дней пользования ссудой  , то использованное в формулах (3) и (4) обозначение количества полных лет
, то использованное в формулах (3) и (4) обозначение количества полных лет  можно будет выразить как
можно будет выразить как 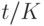 . Подставив это выражение в (3) и (4), получим:
. Подставив это выражение в (3) и (4), получим:
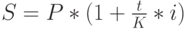 |
( 6) |
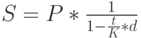 |
( 7) |
В различных случаях могут применяться различные способы подсчета числа дней в году (соглашение по подсчету дней). Год может приниматься равным 365 или 360 дням (12 полных месяцев по 30 дней в каждом). Проблема усугубляется наличием високосных лет. Например, обозначение ACT/360 (actual over 360) указывает на то, что длительность года принимается равной 360 дням. Однако возникает вопрос, а как при этом определяется продолжительность ссуды? Например, если кредит выдается 10 марта со сроком возврата 17 июня этого же года, как считать его длительность – по календарю или исходя из предположения, что любой месяц равен 30 дням? Безусловно, в каждом конкретном случае может быть выбран свой оригинальный способ подсчета числа дней, однако на практике выработаны некоторые общие принципы, знание которых может помочь сориентироваться в любой конкретной ситуации.
