|
Здравствуйте! Записался на ваш курс, но не понимаю как произвести оплату. Надо ли писать заявление и, если да, то куда отправлять? как я получу диплом о профессиональной переподготовке? |
Регрессионное тестирование: методики, не связанные с отбором тестов и методики порождения тестов
Функции предсказания целесообразности
На практике не существует способа в точности предсказать, сколько тестов будет выбрано при минимизации (или по результатам применения любой другой методики отбора тестов). Когда количество тестов, отсеянных по результатам отбора, незначительно, ресурсы, потраченные на отбор тестов, пропадают впустую. В таких случаях говорят, что выборочное регрессионное тестирование нецелесообразно. Чтобы выяснить, заслуживает ли внимания попытка применения выборочного метода регрессионного тестирования, необходимо использовать прогнозирующую функцию.
Прогнозирующие функции основаны на покрытии кода. Для их вычисления используется информация о доле тестов, активирующих покрываемые сущности – операторы, ветви или функции, – что позволяет предсказать количество тестов, которые будут выбраны при изменении этих сущностей. Существует как минимум одна прогнозирующая функция, которая может быть использована для предсказания целесообразности применения безопасной стратегии выборочного регрессионного тестирования.
Пусть P – тестируемая система, S – ее спецификация, T – набор регрессионных тестов для P, а |T| означает число отдельных тестов в T. Пусть М – выборочный метод регрессионного тестирования, используемый для отбора подмножества T при тестировании измененной версии P ; М может зависеть от P, S, T, информации об исполнении T на P и других факторов. Через E обозначим набор рассматриваемых М сущностей тестируемой системы. Предполагается, что T и E непустые, и что каждый синтаксический элемент P принадлежит, по крайней мере, одной сущности из E. Отношение coversM(t, E) определяется как отношение покрытия, достигаемого методом М для P. Это отношение определено над TxE и справедливо тогда и только тогда, когда выполнение теста t на P приводит к выполнению сущности e как минимум один раз. Значение термина "выполнение" определено для всех типов сущностей P. Например, если e – функция или модуль P, e выполняется при вызове этой функции или модуля. Если e – простой оператор, условный оператор, пара определения-использования или другой вид элемента пути в графе выполнения P, e выполняется при выполнении этого элемента пути. Если e – переменная P, e выполняется при чтении или записи этой переменной. Если e – тип P, e выполняется при выполнении любой переменной типа e. Если e – макроопределение P, e выполняется при выполнении расширения этого макроопределения. Если e – сектор P, e выполняется при выполнении всех составляющих его операторов. Соответствующие значения термина "выполнение" могут быть определены по аналогии для других типов сущностей P.
Для данной тестируемой системы P, набора регрессионных тестов T и выборочного метода регрессионного тестирования М можно предсказать, стоит ли задействовать М для регрессионного тестирования будущих версий P, используя информацию об отношении покрытия coversM, достигаемого при использовании М для T и P. Прогноз основан на метрике стоимости, соответствующей P и T. Относительно издержек принимаются некоторые упрощающие предположения.
Пусть EC обозначает множество покрытых сущностей:

Обозначение |EC| используется для числа покрытых сущностей. Иногда удобно представить зависимость coversM(t, E) в виде бинарной матрицы C, строки которой представляют элементы T, а столбцы – элементы E. При этом элемент Ci,j матрицы C определяется следующим образом:
Ci, j = 1, если coversМ(i, j) Ci, j = 0, иначе
Степень накопленного покрытия, обеспечиваемого T, то есть общее число единиц в матрице C, обозначается CC:
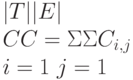
Отметим, что если ограничиться включением в C только столбцов, соответствующих покрытым сущностям EC, накопленное покрытие CC останется неизменным. В частности, для всех непокрытых сущностей u Ci,u равно нулю для всех тестов i (так как coversM(i, u) ложно для всех таких случаев). Следовательно, ограничение на EC при вычислении суммы, определяющей CC, приводит только к исключению слагаемых, равных нулю.
Пусть TM – подмножество T, выбранное М для P, и пусть |TM| обозначает его мощность, тогда  . Пусть sM – удельная стоимость отбора одного теста для TM при применении М к P, и пусть r – удельная стоимость выполнения одного теста из T на P и проверки его результата. М целесообразно использовать в качестве метода отбора тестов тогда и только тогда, когда:
. Пусть sM – удельная стоимость отбора одного теста для TM при применении М к P, и пусть r – удельная стоимость выполнения одного теста из T на P и проверки его результата. М целесообразно использовать в качестве метода отбора тестов тогда и только тогда, когда:
sM|TM| < r(|T| - |TM|), то есть стоимость анализа, необходимого для отбора TM, должна быть меньше стоимости прогона невыбранных тестов,  .
.
Оценка ожидаемого числа тестов, требующих повторного запуска, обозначается NM и вычисляется следующим образом:
Nm = CC/|E|
Использование этой прогнозирующей функции предполагается только в случаях, когда цель выборочной стратегии регрессионного тестирования состоит в повторном выполнении всех тестов, затронутых изменениями, то есть используется безопасный метод отбора тестов. Несколько усовершенствованный вариант оценки NM, использующий в качестве пространства сущностей EC вместо E:
Ncm = CC/|Ec|
Прогнозирующая функция для доли набора тестов, требующей повторного выполнения, то есть для |TM| / |T|, обозначается 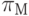 :
:

Прогнозирующая функция 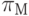 полагается непосредственно на информацию о покрытии. Главные предпосылки, лежащие в основе применения прогнозирующей функции, таковы:
полагается непосредственно на информацию о покрытии. Главные предпосылки, лежащие в основе применения прогнозирующей функции, таковы:
- Целесообразность применения выборочного метода регрессионного тестирования и, как следствие, наша способность к предсказанию целесообразности, непосредственно зависит от доли тестового набора, выбираемой для выполнения методом регрессионного тестирования.
- Эта доля в свою очередь непосредственно зависит от отношения покрытия.
Точность прогнозирующей функции на практике может значительно меняться от версии к версии. Проблема точности может оказаться достаточно серьезной, тем не менее, поскольку прогнозирующая функция используется для долговременного предсказания поведения метода на протяжении нескольких версий, применение средних значений считается допустимым. Отношение coversM(t, e) в ходе сопровождения изменяется очень слабо. По этой причине информация, полученная в результате анализа единственной версии, может оказаться достаточной для управления отбором тестов на протяжении нескольких последовательных новых версий.
Существуют факторы, влияющие на целесообразность отбора тестов, но не учитываемые прогнозирующей функцией. Один из подходов улучшения качества прогноза состоит в использовании информации об истории изменений программы, которую зачастую можно получить из системы управления конфигурацией.
Например, в рис. 12.1 прогнозирующая функция может быть подсчитана как отношение общего количества звездочек в таблице к количеству строк таблицы, т.е. числу покрываемых сущностей. Эта величина составляет 42/11=3.8, т.е. безопасный метод будет отбирать в среднем около 4 тестов. Сведения о методике предсказания суммированы в Табл. 13.4.
| Характеристика | Изменение в результате применения методики |
|---|---|
| Время работы метода отбора в случае, если выборочное тестирование целесообразно | Увеличивается незначительно |
| Время работы метода отбора в случае, если выборочное тестирование нецелесообразно | Уменьшается до пренебрежимо малой величины |
| Снижение точности предсказания от версии к версии | Зависит от объема изменений |
| Результаты применения методики на практике | Положительные (ошибка в 0.8%) |

