Понятие о кодах Боуза-Чоудхури-Хоккенгема
Остался открытым вопрос о методике построения кодов, минимальное расстояние между кодовыми словами которых равно заданному числу. В 1960 году независимо Боуз (Bose), Чоудхури (Chaudhuri) и Хоккенгем (Hocquengem) открыли способ построения полиномиальных кодов, удовлетворяющих таким требованиям. Эти коды получили названия кодов Боуза-Чоудхури-Хоккенгема или БЧХ-кодов (BCH codes). БЧХ-коды могут быть не только двоичными, например, на практике достаточно широко используются недвоичные коды Рида-Соломона (Reed, Solomon), но далее будут рассматриваться только двоичные.
Многочлен  степени
степени  называется примитивным,
если
называется примитивным,
если 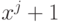 делится на
делится на  без остатка
для
без остатка
для 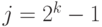 и не делится ни для какого меньшего значения
и не делится ни для какого меньшего значения  .
.
Например, многочлен 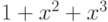 примитивен: он делит
примитивен: он делит 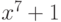 , но не делит
, но не делит 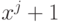 при
при  . Примитивен также многочлен
. Примитивен также многочлен  - он
делит
- он
делит 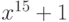 ,
но не делит
,
но не делит 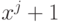 при
при 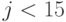 .
.
Кодирующий многочлен  для БЧХ-кода, длина кодовых слов
которого
для БЧХ-кода, длина кодовых слов
которого  ,
строится так. Находится примитивный многочлен минимальной степени
,
строится так. Находится примитивный многочлен минимальной степени  такой, что
такой, что  или
или 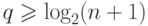 . Пусть
. Пусть  - корень этого многочлена, тогда рассмотрим кодирующий многочлен
- корень этого многочлена, тогда рассмотрим кодирующий многочлен 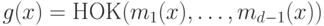 , где
, где 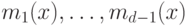 - многочлены минимальной степени, имеющие корнями соответственно
- многочлены минимальной степени, имеющие корнями соответственно 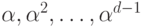 .
.
Построенный кодирующий многочлен производит код с минимальным расстоянием
между кодовыми словами, не меньшим  , и длиной кодовых слов n [1].
, и длиной кодовых слов n [1].
Пример. Нужно построить БЧХ-код с длиной кодовых слов 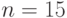 и
минимальным расстоянием между кодовыми словами
и
минимальным расстоянием между кодовыми словами  . Степень примитивного
многочлена равна
. Степень примитивного
многочлена равна 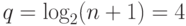 и сам он равен
и сам он равен  .
Пусть
.
Пусть  - его корень, тогда
- его корень, тогда 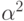 и
и 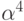 - также его
корни. Минимальным многочленом для
- также его
корни. Минимальным многочленом для  будет
будет 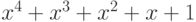 .
Следовательно,
.
Следовательно,

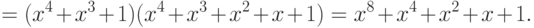
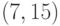 -кодом. Слово 1000100 или
-кодом. Слово 1000100 или 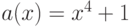 будет
закодировано кодовым словом
будет
закодировано кодовым словом  или
111001100000100.
или
111001100000100.Можно построить11
двоичный БЧХ-код с кодовыми словами длины 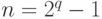 и нечетным минимальным расстоянием
и нечетным минимальным расстоянием  , у которого число
контрольных символов не больше
, у которого число
контрольных символов не больше 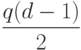 .
.
Первый БЧХ-код, примененный на практике, был 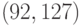 -кодом,
исправляющим ошибки кратности до 5, но наиболее широкое распространение получил
-кодом,
исправляющим ошибки кратности до 5, но наиболее широкое распространение получил 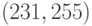 -код, обнаруживающий ошибки кратности до 6.
-код, обнаруживающий ошибки кратности до 6.
БЧХ-коды умеренной длины не слишком далеки от совершенных или квазисовершенных кодов. Коды Хэмминга, например, являются БЧХ-кодами, а БЧХ-коды с минимальным весом кодового слова 5 - квазисовершенны. Но с ростом длины кодовых слов качество БЧХ-кодов падает. Код Голея, например, - это не код БЧХ.
Упражнение 45
Найти кодирующий многочлен БЧХ-кода  с длиной кодовых слов 15
и минимальным расстоянием между кодовыми словами 7. Использовать примитивный
многочлен
с длиной кодовых слов 15
и минимальным расстоянием между кодовыми словами 7. Использовать примитивный
многочлен 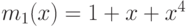 с корнем
с корнем  .
Проверить, будут ли
.
Проверить, будут ли  и
и 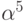 корнями соответственно
многочленов
корнями соответственно
многочленов 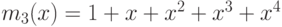 и
и 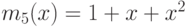 .
.
Циклические избыточные коды
Циклический избыточный код (Cyclical Redundancy Check - CRC)
имеет фиксированную длину и используется для обнаружения ошибок.
Наибольшее распространения получили коды CRC-16 и CRC-32, имеющие длину 16
и 32 бита соответственно. Код CRC строится по исходному сообщению
произвольной длины, т.е. этот код не является блочным в строгом смысле этого
слова. Но при каждом конкретном применении этот код - блочный, 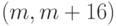 -код для CRC-16 или
-код для CRC-16 или 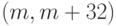 -код для
CRC-32.
-код для
CRC-32.
Вычисление значения кода CRC происходит посредством деления многочлена,
соответствующего исходному сообщению (полином-сообщение), на фиксированный
многочлен (полином-генератор). Остаток от такого деления и есть код CRC,
соответствующий исходному сообщению. Для кода CRC-16 полином-генератор имеет
степень 16, а для CRC-32 - 32. Полиномы-генераторы подбираются специальным
образом и для кодов CRC-16/32 стандартизированы Международным консультативным
комитетом по телеграфной и телефонной связи (CCITT). Для CRC-16, например, стандартным
является полином-генератор 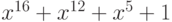 .
.
Пример построения CRC-4 кода для сообщения 11010111, используя
полином-генератор  . Исходному сообщению
соответствует полином
. Исходному сообщению
соответствует полином 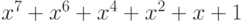 , т.е. нумерация битов здесь начинается
справа.
, т.е. нумерация битов здесь начинается
справа.
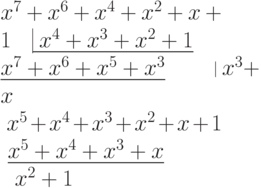
Полиному  соответствуют биты 0101 - это и
есть CRC-4 код.
соответствуют биты 0101 - это и
есть CRC-4 код.
Существуют быстрые алгоритмы для расчета CRC-кодов, использующие специальные таблицы, а не деление многочленов с остатком.
CRC-коды способны обнаруживать одиночную ошибку в любой позиции и, кроме того, многочисленные комбинации кратных ошибок, расположенных близко друг от друга. При реальной передаче или хранении информации ошибки обычно группируются на некотором участке, а не распределяются равномерно по всей длине данных. Таким образом, хотя для идеального случая двоичного симметричного канала CRC-коды не имеют никаких теоретических преимуществ по сравнению, например, с простыми контрольными суммами, для реальных систем эти коды являются очень полезными.
Коды CRC используются очень широко: модемами, телекоммуникационными программами, программами архивации и проверки целостности данных и многими другими программными и аппаратными компонентами вычислительных систем.
Упражнение 46
Построить CRC-4 код для сообщений 10000000 и 101111001, используя
полином-генератор  .
.
