| Казахстан, Алматы |
Рекурсивные функции
Наше доказательство теорем 76 и 77 позволяет также получить такое следствие, называемое иногда теоремой Клини о нормальной форме:
Теорема 78. Всякая частично рекурсивная функция f представима в виде
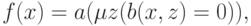
где a и b некоторые примитивно рекурсивные функции.
В самом деле, любая частично рекурсивная функция вычислима на машине Тьюринга, а следовательно, представима в нужном нам виде, как видно из доказательства теоремы 76 (в качестве a берется функция, дающий первый член пары по ее номеру).
Мы сформулировали эту теорему для случая одноместной функции f, но аналогичное утверждение верно и для функций нескольких аргументов (и доказательство почти не меняется).
89.
Покажите, что одним  -оператором, применяя его последним,
не обойтись: не всякая частично рекурсивная функция представима в виде
-оператором, применяя его последним,
не обойтись: не всякая частично рекурсивная функция представима в виде
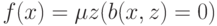
где b некоторая примитивно рекурсивная функция.
Из теоремы Клини о нормальной форме вытекает такое утверждение:
Теорема 79. Всякое перечислимое множество есть проекция примитивно рекурсивного множества.
Перечислимое множество есть область определения рекурсивной функции; представив ее в нормальной форме, видим, что область определения есть проекция множества  .
.
Вычислимость с оракулом
Определение класса частично рекурсивных функций легко
модифицировать для случая вычислимости с оракулом. Пусть имеется
некоторая всюду определенная функция  Рассмотрим класс
Рассмотрим класс ![F[\alpha ]](/sites/default/files/tex_cache/23f4c4beae9eda67fbd998cd736d4d65.png) , который состоит из базисных функций,
функции
, который состоит из базисных функций,
функции  и всех других функций, которые могут быть из
них получены с помощью подстановки, примитивной рекурсии и
минимизации.
и всех других функций, которые могут быть из
них получены с помощью подстановки, примитивной рекурсии и
минимизации.
(Формально можно сказать так: ![F[\alpha ]](/sites/default/files/tex_cache/23f4c4beae9eda67fbd998cd736d4d65.png) есть
минимальный класс, который содержит базисные функции,
функцию
есть
минимальный класс, который содержит базисные функции,
функцию  и замкнут относительно подстановки, примитивной
рекурсии и минимизации. Такой минимальный класс существует
достаточно взять пересечение всех классов с этими свойствами.)
и замкнут относительно подстановки, примитивной
рекурсии и минимизации. Такой минимальный класс существует
достаточно взять пересечение всех классов с этими свойствами.)
Теорема 80. Класс ![F[\alpha ]](/sites/default/files/tex_cache/23f4c4beae9eda67fbd998cd736d4d65.png) состоит из всех функций, вычислимых
с оракулом
состоит из всех функций, вычислимых
с оракулом  (то есть с помощью программ,
вызывающих
(то есть с помощью программ,
вызывающих  как внешнюю процедуру).
как внешнюю процедуру).
Прежде всего заметим, что все функции из класса ![F[\alpha ]](/sites/default/files/tex_cache/23f4c4beae9eda67fbd998cd736d4d65.png) вычислимы с помощью таких программ. Это можно объяснить,
например, так. Программы с конечным числом переменных вычисляли
все частично-рекурсивные функции. Если добавить к ним
примитивную операцию вычисления значения функции
вычислимы с помощью таких программ. Это можно объяснить,
например, так. Программы с конечным числом переменных вычисляли
все частично-рекурсивные функции. Если добавить к ним
примитивную операцию вычисления значения функции  в
заданной точке, то они точно так же будут вычислять все функции
из класса
в
заданной точке, то они точно так же будут вычислять все функции
из класса ![F[\alpha ]](/sites/default/files/tex_cache/23f4c4beae9eda67fbd998cd736d4d65.png) .
.
Более содержательно обратное утверждение: мы хотим доказать, что
если некоторая (частичная, вообще говоря) функция вычислима
относительно 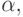 то она может быть получена из базисных
функций и из
то она может быть получена из базисных
функций и из  с помощью подстановки, рекурсии и
минимизации.
с помощью подстановки, рекурсии и
минимизации.
Для этого вспомним критерий относительной вычислимости (теорема 45).
Пусть функция f вычислима относительно всюду определенной
функции  Тогда, как мы знаем, существует перечислимое
множество W троек вида
Тогда, как мы знаем, существует перечислимое
множество W троек вида  , где x и y натуральные числа, а t образцы (функции с конечной областью
определения), которое является корректным (тройки с
одинаковым x, но разными y содержат несовместные
образцы) и
для которого
, где x и y натуральные числа, а t образцы (функции с конечной областью
определения), которое является корректным (тройки с
одинаковым x, но разными y содержат несовместные
образцы) и
для которого
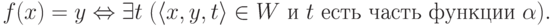
Мы сейчас покажем, что свойство " t есть часть
функции  " является примитивно рекурсивным
относительно
" является примитивно рекурсивным
относительно 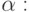 его характеристическая функция получается из
базисных
функций и из
его характеристическая функция получается из
базисных
функций и из  с помощью операций подстановки и рекурсии.
(Напомним, что мы отождествляем образцы с их номерами в какой-то
нумерации; о ее выборе см. ниже.)
с помощью операций подстановки и рекурсии.
(Напомним, что мы отождествляем образцы с их номерами в какой-то
нумерации; о ее выборе см. ниже.)
После этого останется записать W как проекцию примитивно
рекурсивного множества (  , где v примитивно рекурсивна),
и заметить, что
, где v примитивно рекурсивна),
и заметить, что

Здесь v' примитивно рекурсивная относительно  функция, для которой v'(x,[y,t,u])=0 тогда и только тогда,
когда v(x,y,t,u)=0 и t есть часть
функции
функция, для которой v'(x,[y,t,u])=0 тогда и только тогда,
когда v(x,y,t,u)=0 и t есть часть
функции 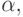 а
функция p1 выделяет из номера тройки [y,t,u] ее
первый
член y.
а
функция p1 выделяет из номера тройки [y,t,u] ее
первый
член y.
Осталось показать, что множество  является примитивно рекурсивным
относительно
является примитивно рекурсивным
относительно  При доказательстве мы будем предполагать,
что нумерация
образцов такова, что следующие функции примитивно рекурсивны (они
определены для образцов с непустой областью определения; для
пустого образца доопределим их как угодно):
При доказательстве мы будем предполагать,
что нумерация
образцов такова, что следующие функции примитивно рекурсивны (они
определены для образцов с непустой областью определения; для
пустого образца доопределим их как угодно):
- last-x(t) наибольшее из чисел, на котором определен образец с номером t ;
- last-y(t) значение функции-образца с номером t в максимальной точке своей области определения;
- all-but-last(t) номер образца, который получится из образца с номером t, если удалить максимальную точку области определения.
Тогда можно записать такое рекурсивное определение: образец с
номером t есть часть функции 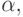 если либо этот
образец пуст, либо
если либо этот
образец пуст, либо 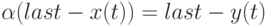 и образец с номером all-but-last(t) есть часть
функции
и образец с номером all-but-last(t) есть часть
функции 
Это определение использует " возвратную рекурсию",
которая разобрана в теореме 74;
значение
функции определяется рекурсивно через ее значения в меньших
точках. Надо только выбрать нумерацию образцов так, чтобы all-but-last(t) было меньше t
для всех t. Этого
несложно добиться: например, можно нумеровать образцы с помощью
простых чисел, считая, что образец 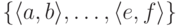 имеет номер pa(b+1)... pe(f+1), где pi простое
число с номером i (так что p0=2, p1=3, p2=5, ...).
имеет номер pa(b+1)... pe(f+1), где pi простое
число с номером i (так что p0=2, p1=3, p2=5, ...).
Заметим, что доказательство стало бы немного
проще, если использовать
только " сплошные образцы" (областью определения которых
является некоторый начальный отрезок натурального ряда)
тогда можно начать с того, что установить примитивную
рекурсивность (относительно  ) функции n
) функции n 
![[\alpha (0),\alpha (1),\dots ,\alpha (n)]](/sites/default/files/tex_cache/f665627a0af2d54cb993c8ceaa3d93f5.png) . Легко понять также, что
в определении относительной вычислимости можно ограничиться
только сплошными образцами.
. Легко понять также, что
в определении относительной вычислимости можно ограничиться
только сплошными образцами.
