Арифметичность вычислимых функций

Арифметичность вычислимых функций

Сейчас мы докажем, что функции, вычислимые программами с конечным числом переменных, арифметичны, то есть их графики являются арифметическими множествами. В этом разделе мы вновь предполагаем некоторое знакомство читателя с логическими обозначениями, и будем рассматривать арифметические формулы, содержащие переменные по натуральным числам, равенство, константы 0 и 1, операции сложения и умножения, логические связки (И, ИЛИ, НЕ) и кванторы " для всех" и " существует". Формально говоря, мы рассматриваем сигнатуру, содержащую единственный двуместный предикатный символ (равенство), две константы 0 и 1 и два двуместных функциональных символа (сложение и умножение). Говоря об истинности таких формул, мы имеем в виду их истинность в стандартной интерпретации, носителем которой является множество N натуральных чисел.

Множество 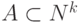называется арифметическим, если существует арифметическая формула с параметрами x₁,...,x_k, которая его представляет в следующем смысле: 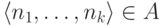тогда и только тогда, когда формула истинна при значениях параметров x₁=n₁,..., x_k=n_k.

Теорема 67. График любой функции, вычисляемой программой с конечным числом переменных, является арифметическим множеством.

Пусть f : N -> N функция, вычислимая некоторой программой P с конечным числом переменных k₁,...,k_N. Будем считать, что входной переменной является k₁, а выходной k₂. Нам нужно написать формулу с двумя переменными x, y, которая была бы истинна тогда и только тогда, когда y=f(x). Состояние программы с конечным числом переменных полностью описывается значениями переменных и номером текущей команды (в процессорах соответствующий регистр часто называют program counter, по-русски счетчик команд). Легко понять, что соответствие между двумя последовательными состояниями программы с конечным числом переменных арифметично. Мы имеем в виду, что можно написать арифметическую формулу

Step(s1,...,sN,p,s1',...,sN',p'),

с 2N+2 переменными, которая утверждает, что данная программа P из состояния, где переменные равны s₁,...,s_N, а счетчик команд равен p, за один шаг переходит в состояние, где переменные равны s₁',...,s_n', а счетчик команд равен p'. (Договоримся, что значение p'=0 соответствует остановке программы.) Такая формула является конъюнкцией отдельных утверждений, соответствующих каждой строке программы. Пусть, например, строка 7 программы имеет вид k₂:=k₃. Тогда в конъюнкции будет член вида

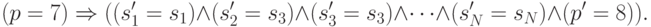
Для строки с условными переходами типа

3  if k5=0 then goto 17 else goto 33

в формуле будет два конъюнктивных члена (на два случая перехода)

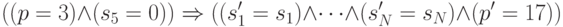
и

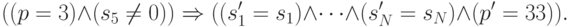
Надо еще добавить утверждение о том, что при p=0 работа прекращается, то есть что переменные на следующем шаге сохраняют свои значения, и p' остается равным 0.

Таким образом, арифметичность одного шага работы программы доказать несложно. Остается главный вопрос: как записать в виде формулы тот факт, что существует последовательность шагов, которая начинается с исходного состояния, заканчивается в данном и в которой каждый шаг правилен. Трудность в том, что здесь нужно как бы написать переменное число кванторов существования или квантор " существует конечная последовательность натуральных чисел".

Это делается с помощью приема, традиционно называемого -функцией Геделя. Вот что имеется в виду.

Лемма 1. Для любого k можно найти сколь угодно большое целое положительное число b, при котором первые k членов последовательности b+1, 2b+1, 3b+1,... попарно взаимно просты.

Доказательство. Любой общий простой делитель двух из этих чисел будет делителем их разности, то есть числа lb при 0<l<k ; взяв b кратным k!, мы гарантируем, что он будет делителем числа b, но все члены нашей последовательности взаимно просты с b. Лемма доказана.

Лемма 2. Для любой последовательности x₀,x₁,...,x_n натуральных чисел можно найти такие числа a и b, что x_i есть остаток от деления a на b(i+1)+1.

Доказательство. Согласно предыдущей лемме, делители b(i+1)+1 можно взять взаимно простыми (и сколь угодно большими), остается воспользоваться " китайской теоремой об остатках". Эта теорема утверждает, что если целые положительные числа d₁,...,d_k взаимно просты, то при делении целого u на них может получиться любой заданный набор остатков. В самом деле, таких наборов будет d₁d₂... d_k (поскольку при делении на d_i возможны остатки от 0 до d_i-1 ). При делении чисел u=0,1,...,d₁d₂... d_k-1 получаются разные наборы остатков (если два числа u' и u'' дают одинаковые остатки, то их разность делится на все d_i, что невозможно в силу взаимной простоты). Поэтому чисел столько же, сколько наборов остатков, и должны появиться все наборы. Лемма 2 доказана.

Эта лемма показывает, что последовательность произвольной длины можно закодировать тремя числами a, b и n (последнее число длина последовательности). Таким образом, условно говоря, можно заменить " формулу"

(которая на самом деле не является арифметической формулой, так как содержит квантор по конечным последовательностям) на формулу

Мы будем записывать остаток от деления a на b(i+1)+1 как (отсюда и название " бета-функция").

Возвращаясь к нашей программе P с конечным числом переменных k₁,...,k_N и вычисляемой ей функции f, можно записать утверждение вида f(x)=y так: существуют такое число шагов n и такие числа a₁,b₁,a₂,b₂,...,a_N,b_N,a,b, что

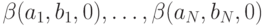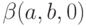• есть правильные начальные значения переменных (первое равно x, остальные равны 0 ); есть правильное начальное значения счетчика команд, то есть 1 ;
• для каждого i от 0 до n-1 имеет место
  
  то есть каждый переход соответствует программе;
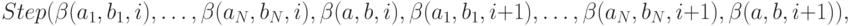
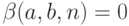• (значение выходной переменной k₂ в конце вычисления равно y ) и (значение счетчика команд в конце вычисления равно 0, что по нашей договоренности соответствует остановке машины).

Итак, арифметичность вычислимых (на машинах с конечным числом переменных) функций доказана.

Вспоминая теорему 65, мы заключаем, что всякая вычислимая на машине Тьюринга функция арифметична. Принимая тезис Тьюринга, можно сказать, что график любой вычислимой функции является арифметическим множеством.