Машины Тьюринга

Ассоциативные исчисления

Сейчас мы используем машины Тьюринга, чтобы доказать неразрешимость некоторой алгоритмической проблемы, связанной с так называемыми ассоциативными исчислениями.

Напомним, что алфавитом называют конечное множество, элементы его называют символами, или буквами, а конечные последовательности букв словами.

Пусть фиксирован алфавит A. Будем называть правилом произвольную запись вида P -> Q, где P и Q слова этого алфавита (мы считаем, что сама стрелка не является буквой алфавита). Будем называть ассоциативным исчислением конечный набор правил. (Порядок правил в наборе не играет роли.) Каждое правило рассматривается как правило преобразования слов. Именно, мы говорим, что к слову X можно применить правило P -> Q, если в слове X есть участок из подряд идущих букв (подслово), совпадающий с P. В этом случае его разрешается заменить на Q. Таких участков может быть несколько, так что к одному и тому же слову можно применить одно и то же правило несколькими разными способами. Кроме того, в исчислении может быть несколько правил, применимых к данному слову, и тогда можно применять любое из них. После этого можно снова применить то же самое или другое правило исчисления, и так далее.

Повторим это определение более формально. Говорят, что слово X можно преобразовать в слово Y по правилам исчисления I, если существует конечная последовательность слов

X = Z0, Z1, Z2, ..., Zk-1, Zk = Y,

в которой каждое слово Z_i получается из предыдущего слова Z_i-1 по одному из правил исчисления I, то есть в I существует такое правило P -> Q, что Z_i-1=RPS и Z_i=RQS для некоторых слов R и S.

Таким образом, каждому исчислению соответствует некоторое множество пар слов множество таких пар , что X можно преобразовать в Y по правилам этого исчисления.

Теорема 60. Для всякого исчисления это множество перечислимо. Существует исчисление, для которого это множество неразрешимо.

Мы докажем эту теорему в следующем разделе. Первая ее часть доказывается легко: множество всех последовательностей Z₀ -> Z₁ -> ... -> Z_k, согласованных с правилами исчисления, разрешимо и потому перечислимо. Если от каждой из них оставить только начало и конец, получится перечисление искомого множества.

Осталось построить пример неразрешимого ассоциативного исчисления (исчисления, для которого указанное множество неразрешимо). Для этого мы покажем, что работу любой машины Тьюринга можно в некотором смысле моделировать с помощью ассоциативного исчисления, а затем возьмем исчисление, соответствующее машине с неразрешимой проблемой остановки.

Моделирование машин Тьюринга

Теорема 61. Пусть M машина Тьюринга, алфавит которой включает 0 и 1. Тогда можно построить ассоциативное исчисление I с таким свойством: двоичное слово Y является результатом работы машины на двоичном слове X тогда и только тогда, когда слово [ X ] по правилам исчисления I можно преобразовать в слово Y.

Напомним, что результат работы машины мы определили как максимальный блок нулей и единиц, начиная с позиции головки. Заметим также, что алфавит исчисления I содержит символы 0 и 1, дополнительные символы [ и ] и может содержать другие символы.

  78. Покажите, что если без дополнительных символов [ и ] утверждение теоремы не будет верным. (Указание: если слово Y можно получить из слова X по правилам исчисления, то слово PYQ можно получить из слова PXQ по правилам исчисления.)

Идея моделирования состоит в следующем. Будем кодировать конфигурацию машины Тьюринга (содержимое ленты, положение головки, состояние) в виде слова. Тогда переход от конфигурации к следующей по правилам машины Тьюринга соответствует применению правила ассоциативного исчисления.

Конечно, для этого надо правильно выбрать кодирование. Мы будем делать это так: конфигурация

кодируется словом [ P s Q ]. Таким образом, алфавит нашего исчисления будет включать все буквы алфавита машины Тьюринга, включая пробел (который мы изображаем как " _ "), и все ее состояния (мы считаем, что множество состояний не пересекается с алфавитом), а также специальные символы [ и ]. Заметим, что кодирование не однозначно за счет того, что слово P может начинаться с пробела, а слово Q им кончаться. Например, если a, b и c буквы алфавита, а s состояние, то слово [absc] соответствует состоянию s, ленте ...abc... и головке напротив c ; слова [_absc] и [absc_] соответствуют той же конфигурации. Другие примеры кодирования конфигураций: слово [sabc] соответствует состоянию s, ленте ...abc... и головке напротив a, слово [abcs] ленте ...abc... c головкой справа от c, а слово [s] соответствует пустой ленте.

Теперь надо написать правила нашего исчисления. Мы хотим, чтобы к коду любой конфигурации было применимо ровно одно правило и чтобы получающееся при его применении слово было кодом следующей конфигурации. Это можно сделать, построчно переводя таблицу переходов машины Тьюринга на язык правил. Пусть, например, в таблице есть инструкция " находясь в состоянии s и читая букву x, перейти в состояние s', напечатать букву x' и остаться на месте". Тогда мы включаем в наше исчисление правило

s x -> s'x'.

Инструкция " находясь в состоянии s и читая букву x, перейти в состояние s', напечатать букву x' и сдвинуться влево" порождает правила

для всех букв алфавита машины Тьюринга.

Инструкция " находясь в состоянии s и читая букву x, перейти в состояние s', напечатать букву x' и сдвинуться вправо" порождает правило

s x -> x's'.

Но надо еще позаботиться о ситуации, когда слова P или Q пусты. Для этого нужны такие правила:

если в таблице есть инструкция...	правило
читая x в состоянии s, перейти в состояние s', напечатать x' и сдвинуться налево	[ s x -> [ s' _x'
читая пробел в состоянии s, перейти в состояние s', напечатать x' и остаться на месте	s ] -> s' x' ]
читая пробел в состоянии s, перейти в состояние s', напечатать x' и сдвинуться налево
читая пробел в состоянии s, перейти в состояние s', напечатать x' и сдвинуться направо	s ] -> x' s' ]

Особые случаи, рассмотренные в этой таблице это случай пробела под головкой и пустого слова Q, а также сдвига налево при пустом слове P.

Применение этих правил шаг за шагом моделирует процесс вычисления машины Тьюринга. Но надо еще " подготовить вход" и " очистить выход". После завершения работы машина оказывается в некотором заключительном состоянии s, и код конфигурации имеет вид [PsQ]. А нам надо получить слово, являющееся результатом работы машины. То есть, по нашим правилам определения результата, надо удалить P и открывающуюся скобку, а также в Q выделить максимальное начало из нулей и единиц, и все последующее удалить. Вот как это делается. 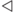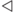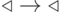Введем дополнительный символ , правила s -> для каждого заключительного состояния s, правила для всех букв и правило 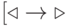. Тогда символ 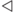появится на месте заключительного состояния, съест все слева от себя, а в конце встретит скобку и превратится в новый символ . Для этого символа мы используем правила , и (последнее правило для всех из алфавита машины, кроме 0 и 1, а также для ). Символ пропускает результат налево от себя и превращается в символ . А этот символ уничтожает все справа от себя и затем самоуничтожается в паре с закрывающейся скобкой; правила таковы: 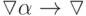для всех символов из алфавита машины, а также ( обозначает пустое слово).

Эти правила позволяют выделить результат работы машины из кода заключительной конфигурации. Теперь уже можно сказать, что машина на входе X дает результат Y тогда и только тогда, когда по этим правилам из слова [s₀ X] можно получить слово Y. Единственное различие с формулировкой теоремы состоит в том, что там нет символа s₀, но это исправить легко: добавим еще один символ [', правило [-> ['s₀, и во всех остальных правилах заменим [ на ['.

Теперь уже все в точности соответствует формулировке теоремы, и доказательство можно считать завершенным. (Увы, аккуратное проведение почти очевидной идеи часто требует перечисления многих деталей, в которых к тому же легко пропустить какой-нибудь случай или допустить ошибку.)

Теперь уже можно построить обещанное неразрешимое ассоциативное исчисление.

Возьмем перечислимое неразрешимое множество K. Возьмем машину Тьюринга, которая на входах из K останавливается и дает пустое слово, а на входах не из K не останавливается (полухарактеристическая функция перечислимого множества, напомним, вычислима, и потому вычислима на машине Тьюринга по тезису Тьюринга).

Построим ассоциативное исчисление, моделирующее эту машину в только что описанном смысле. Для него нет алгоритма, который по паре слов X и Y выясняет, можно ли преобразовать X в Y. В самом деле, если бы такой алгоритм был, то можно было бы применить его к словам [X] и (пустое слово) и узнать, лежит ли слово X в множестве K или не лежит.