Основы теории вычислимых функций

:

Основы теории вычислимых функций
[+]
Опубликован: 16.03.2007 | Уровень: профессионал | Доступ: платный
Лекция 8:

Арифметическая иерархия
A
|
версия для печати
< Лекция 7 || Лекция 8: 1234 || Лекция 9 >

  68. Докажите, что если A принадлежит классу \Sigma _{n} [ \Pi _{n} ], то и множество \in tersect(A) номеров конечных множеств, пересекающихся с A, принадлежит классу \Sigma _{n} [ \Pi _{n} ].

  69. Пусть свойство R(x,y) пар натуральных чисел принадлежит классу \Sigma _{n}. Покажите, что свойство

S(x)= (\forall y \le x),\ R(x,y)

принадлежит \Sigma _{n}. (Ограниченный квантор (\forall y \le x) читается как " для всех y, не превосходящих x ".)

Переходя к дополнениям, мы немедленно получаем такое утверждение:

Лемма 2. Если A принадлежит классу \Sigma _{n} [ \Pi _{n} ], то множество Disjoint(A), состоящее из номеров конечных множеств, не пересекающихся с A, принадлежит \Pi _{n} [ \Sigma _{n} ].

Доказательство леммы. Не пересекаться с A означает быть подмножеством дополнения к A, и остается воспользоваться предыдущей леммой и тем, что дополнение к множеству из класса \Sigma _{n} [ \Pi _{n} ] лежит в классе \Pi _{n} [ \Sigma _{n} ]. Лемма доказана.

Теперь мы можем перейти к доказательству того факта, что все множества, перечислимые относительно 0(n-1), принадлежат классу \Sigma _{n}. Это также доказывается индукцией по n.

Начнем с первого нетривиального случая: почему множество, перечислимое относительно 0', лежит в \Sigma _{2}? (Здесь можно было бы применить критерий 0' -вычислимости, приведенный выше, но мы предпочитаем действовать по общей схеме, которая годится и для больших n.)

Итак, пусть некоторое множество A перечислимо относительно 0'. Тогда оно перечислимо относительно некоторого перечислимого множества B, то есть перечислимо относительно характеристической функции b множества B. Согласно доказанному нами выше критерию (теорема 45), это означает, что существует перечислимое множество Q пар вида 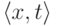\langle x,t\rangle, где x число, а t образец, для которого

x \in A \Leftrightarrow \exists t [\text{($\langle x,t\rangle \in Q$) и ($b$~продолжает~$t$)}].

Без ограничения общности можно считать, что образец t представляет собой функцию, определенную на конечном множестве и принимающую значения 0 и 1. (Если у t есть какие-то другие значения, то он не может быть частью характеристической функции множества B и роли не играет.) Условие " b продолжает t " в терминах множества B звучит так: B содержит множество тех аргументов, на которых t принимает значение 1, и не пересекается с множеством тех аргументов, на которых t принимает значение 0. Поэтому вместо образцов можно говорить о парах конечных множеств; тогда вместо Q надо рассмотреть перечислимое множество P троек вида \langle x,u,v \rangle и написать так:

\begin{multiline*} x \in A \Leftrightarrow \exists u\exists v [\text{($\langle x,u,v\rangle \in P$) и ($D_u$~содержится в~$B$)}\\ \text{и ($D_v$~не пересекается с~$B$)}]. \end{multiline*}

Теперь вместо " Du содержится в B " напишем " u \in opSubset(B) ", а вместо " Dv не пересекается с B " напишем " v \in Disjoint(B) ". Остается заметить, что все три свойства, соединенные союзом " и" в правой части, принадлежат классу \Sigma _{2} и даже меньшим классам. Именно, первые два принадлежат классу \Sigma _{1}, так как P и B перечислимы (для второго свойства применяем лемму 1). Третье же принадлежит классу \Pi _{1} по лемме 2. Поэтому их конъюнкция принадлежит классу \Sigma _{2}, и операция проекции (кванторы \exists\ u\ \exists\ v ) не выводит за пределы этого класса. Случай n=2 разобран.

Далее, если какое-то множество A перечислимо относительно 0'', то по определению это означает, что оно перечислимо относительно некоторого B, которое перечислимо относительно 0' и потому лежит в \Sigma _{2}. После этого все рассуждения проходят точно так же со сдвигом на 1. Аналогично разбираются и все следующие значения n.

Из доказанной теоремы немедленно вытекает такое следствие:

Теорема 57. Пересечение классов \Sigma _{n} \cap \Pi _{n} совпадает с классом разрешимых относительно 0(n-1) множеств.

В самом деле, релятивизованная теорема Поста (теорема 2) утверждает, что некоторое множество является X -разрешимым тогда и только тогда, когда оно и его дополнение X -перечислимы (здесь X произвольный оракул).

Теорема 58. Класс \Sigma _{n} \cup \Pi _{n} является собственным подмножеством класса \Sigma _{n+1} \cap \Pi _{n+1}.

Вспомним, что такое 0(n). Это степень множества X, являющегося m -полным в классе 0(n-1) -перечислимых множеств. Поскольку X является m -полным в указанном классе, оно не 0(n-1) -разрешимо, то есть его дополнение не является 0(n-1) -перечислимым.

Значит, по доказанной только что теореме X принадлежит классу \Sigma _{n}, а его дополнение нет. Напротив, дополнение к X принадлежит \Pi _{n}, но не \Sigma _{n}. Рассмотрим теперь " соединение" множества X с его дополнением, е множество

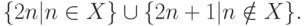
\{ 2n | n \in X\} \cup \{ 2n+1 | n \notin X\} .

К этому множеству m -сводятся как X, так и его дополнение, поэтому оно не может принадлежать ни \Sigma _{n}, ни \Pi _{n}. С другой стороны, оно, очевидно, разрешимо относительно X, поэтому по доказанной теореме принадлежит и \Sigma _{n+1}, и \Pi _{n+1}.

Дальше >>
< Лекция 7 || Лекция 8: 1234 || Лекция 9 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 13
Жансерик Амзеев
Жансерик Амзеев
Казахстан, Алматы
предложить дружбу
Виталий Федоров
Виталий Федоров
Россия, Ярославская область
предложить дружбу