| Казахстан, Алматы |
Универсальные функции и неразрешимость
Перечислимое неразрешимое множество
Теперь мы можем доказать обещанное утверждение.
Теорема 11.Существует перечислимое неразрешимое множество. (Переформулировка: существует перечислимое множество с неперечислимым дополнением.)
Рассмотрим вычислимую функцию f(x), не имеющую всюду определенного вычислимого продолжения. Ее область определения F будет искомым множеством. В самом деле, F перечислимо (по одному из определений перечислимости). Если бы F было разрешимо, то функция
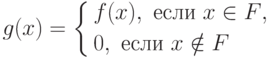
была бы вычислимым всюду определенным продолжением функции f (при вычислении g(x) мы сначала проверяем, лежит ли x в F, если лежит, то вычисляем f(x) ).
Полезно проследить, какое именно множество в итоге оказалось перечислимым и неразрешимым. Легко понять, что это множество тех n, при которых U(n,n) определено. Если вспомнить конструкцию функции U, то это множество тех n, при которых n -я программа останавливается на n. Поэтому иногда говорят, что " проблема самоприменимости " (применимости программы к своему номеру) неразрешима.
Заметим, что отсюда следует, что и область определения всей универсальной функции U является перечислимым неразрешимым множеством пар. (Если бы проблема выяснения применимости программы к произвольному аргументу была бы разрешима, то и ее частный случай применимость программы к себе был бы разрешим.)
Эту более общую и более естественную, чем выяснение самоприменимости, задачу (узнать, остановится ли данная программа на данном входе) называют иногда " проблемой остановки". (Многие слушатели курсов по логике и теории алгоритмов помнят таинственные и грозные слова " Проблема остановки для машин Тьюринга алгоритмически неразрешима", даже забыв все остальное.)
20. Пусть U перечислимое множество пар натуральных чисел, универсальное для класса всех перечислимых множеств натуральных чисел. Докажите, что его " диагональное сечение " 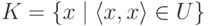 является перечислимым неразрешимым множеством.
является перечислимым неразрешимым множеством.
21. Некоторое множество S натуральных чисел разрешимо. Разложим все числа из S на простые множители и составим множество D всех простых чисел, встречающихся в этих разложениях. Можно ли утверждать, что множество D разрешимо?
22. Множество 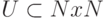 разрешимо. Можно ли утверждать, что множество " нижних точек " множества U, то есть множество
разрешимо. Можно ли утверждать, что множество " нижних точек " множества U, то есть множество
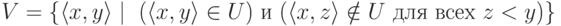
является разрешимым? Можно ли утверждать, что V перечислимо, если U перечислимо?
23. Покажите, что существуют перечислимые снизу, но не вычислимые числа в смысле определений, данных на с. (Указание. Рассмотрим сумму ряда 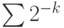 по всем k из какого-либо перечислимого множества P. Она всегда перечислима снизу, но будет вычислимой только при разрешимом P.)
по всем k из какого-либо перечислимого множества P. Она всегда перечислима снизу, но будет вычислимой только при разрешимом P.)
Мы вернемся к вычислимым действительным числам в задачах 31 и 61.
Перечислимые неотделимые множества
Небольшая модификация рассуждения позволяет доказать усиление доказанной выше теоремы:
Теорема 12.Существует вычислимая функция, принимающая только значения 0 и 1 и не имеющая всюду определенного вычислимого продолжения.
Вместо функции d'(x) = d(x) + 1 можно рассмотреть функцию
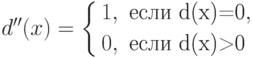
(имеется в виду, что d''(x) не определено, если d(x) не определено). Тогда любое всюду определенное продолжение функции d'' будет по-прежнему отличаться от d всюду и потому не будет вычислимым.
Этот результат можно перевести на язык перечислимых множеств. Говорят, что два непересекающихся множества X и Y отделяются множеством C, если множество C содержит одно из них и не пересекается с другим.
Теорема 13.Существуют два непересекающихся перечислимых множества X и Y, которые не отделяются никаким разрешимым множеством.
В самом деле, пусть d вычислимая функция, принимающая только значения 0 и 1 и не имеющая всюду определенного вычислимого продолжения. Пусть X = {x | d(x) = 1} и Y = {x | d(x) = 0}. Легко видеть, что множества X и Y перечислимы. Пусть они отделяются разрешимым множеством C ; будем считать, что C содержит X и не пересекается c Y (если наоборот, перейдем к дополнению). Тогда характеристическая функция множества C (равная 1 внутри C и 0 вне него) продолжает d.
Заметим, что этот результат усиливает утверждение о существовании перечислимого неразрешимого множества (если два множества не отделимы разрешимыми множествами, то ни одно из них не разрешимо).
24. Как описать построенные перечислимые неотделимые множества в терминах универсальной функции U(n,x)?
25. Покажите, что существует счетное число непересекающихся перечислимых множеств, никакие два из которых нельзя отделить разрешимым множеством.
Простые множества: конструкция Поста
Существуют и другие конструкции перечислимых неразрешимых множеств. Вот одна из них (предложенная Э.Постом).
Назовем множество иммунным, если оно бесконечно, но не содержит бесконечных перечислимых подмножеств. Перечислимое множество называют простым, если его дополнение иммунно. (Очевидно, такое множество не может быть разрешимым.)
Теорема 14.Существует простое множество.
Нам нужно, чтобы перечислимое множество S имело иммунное дополнение. Это означает, что S должно пересекаться с любым бесконечным перечислимым множеством. Чтобы гарантировать это, полезно для каждого перечислимого множества V добавить какой-то его элемент в S (хотя бы для бесконечных V ). При этом надо позаботиться о том, чтобы вне S осталось бесконечно много элементов. Это можно гарантировать, если добавлять достаточно большие элементы (например, из множества номер i добавлять только один элемент, притом больший 2i ).
Объясним конструкцию подробнее. Пусть W универсальное перечислимое множество пар, среди сечений Wi которого встречаются все перечислимые множества натуральных чисел. Будем называть Wi " перечислимым множеством номер i " (при этом разным номерам может соответствовать одно и то же множество). Рассмотрим множество пар  . Это множество перечислимо (как пересечение W и разрешимого множества
. Это множество перечислимо (как пересечение W и разрешимого множества 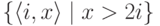 ). Перечисляя его, будем отбрасывать пары, у которых первый член уже встречался ранее. Останется некоторое перечислимое подмножество
). Перечисляя его, будем отбрасывать пары, у которых первый член уже встречался ранее. Останется некоторое перечислимое подмножество 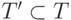 . Рассмотрим теперь перечислимое множество S вторых членов пар, входящих в T'.
. Рассмотрим теперь перечислимое множество S вторых членов пар, входящих в T'.
Это множество пересекается с любым бесконечным перечислимым множеством. В самом деле, если Wi бесконечно, то оно содержит и числа, большие 2i, поэтому в T (а, значит, и в T' ) есть пары с первым членом i. Второй член такой пары из T' будет лежать и в S, и в Wi.
С другой стороны, множество S имеет бесконечное дополнение, поскольку среди чисел от 0 до 2n - 1 максимум n различных чисел могут принадлежать S (это числа, попавшие в S c одной из первых n вертикалей все остальные будут уже больше 2n ).
26. Докажите, что бесконечное множество, не содержащее бесконечных разрешимых подмножеств, иммунно.
27. Докажите, что существует перечислимое множество, для которого прямой пересчет (последовательность элементов в порядке возрастания без повторений) его дополнения не ограничен сверху никакой всюду определенной вычислимой функцией. Докажите, что это множество является простым.
