|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Объектно-ориентированное программирование
9.3 Наследование и полиморфизм
Второй основополагающей составляющей объектно-ориентированного программирования является наследование. Смысл наследования заключается в следующем: если нужно создать новый класс, лишь немного отличающийся от старого, то нет необходимости в переписывании заново уже существующих полей и методов. В этом случае объявляется новый класс, который является наследником уже имеющегося, и к нему добавляются новые поля, методы и свойства. При создании новый класс является наследником членов ранее определённого базового класса (родителя). Класс-наследник является производным от базового, причём он сам может выступать в качестве базового класса для вновь создаваемых классов.
В Object Pascal все классы являются потомками класса TObject. Поэтому если вы создаёте дочерний класс непосредственно от класса TObject, то в определении его можно не упоминать.
Производный класс наследует от класса-предка поля и методы. Если имеет место совпадение имён методов, то говорят, что они перекрываются. В зависимости от того, какие действия происходят при вызове, методы делятся на следующие группы:
- статические методы;
- виртуальные методы;
- динамические методы.
По умолчанию все методы статические. Эти методы полностью перекрываются в классах-потомках при их переопределении. При этом можно полностью изменить объявление метода. Если обращаться к такому методу у объекта базового класса, то будет работать метод класса-родителя. Если обращаться к методу у производного класса, то будет работать новый метод.
Виртуальные и динамические методы имеют в базовом и производном классе те же имена и типы. В классах-наследниках эти методы перегружены. В зависимости от того, с каким классом работают, соответственно и вызывается метод этого класса.
Основная разница между виртуальными и динамическими методами — в способе их вызова. Информация о виртуальных методах хранится в таблице виртуальных методов VMT. В VMT хранятся виртуальные методы данного класса и всех его предков. При создании потомка класса вся VMT предка переносится в потомок и там к ней добавляются новые методы. Поиск нужного метода занимает мало времени, так как класс имеет всю информацию о своих виртуальных методах. Динамические методы не дублируются в таблице динамических методов DMT потомка. DMT класса содержит только методы, объявленные в этом классе. При вызове динамического метода сначала осуществляется поиск в DMT данного класса, и если метод не найден — то в DMT предка класса и т. д. Таким образом использование виртуальных методов требует больший расход памяти из-за необходимости хранения массивных VMT всех классов, зато они вызываются быстрее.
Изменяя алгоритм того или иного метода в производных классах, программист может придавать этим потомкам отсутствующие у родителя специфические свойства. Для изменения метода необходимо перегрузить его в потомке, т. е. объявить в наследнике одноимённый метод и реализовать в нём нужные действия. В результате в объекте-родителе и объекте-потомке будут действовать два одноимённых метода, имеющих разную алгоритмическую основу. Это называется полиморфизмом объектов.
Виртуальные и динамические методы объявляются так же, как и статические, только в конце описания метода добавляются служебные слова virtual или dynamic:
type
...
...
end;
Чтобы перегрузить в классе-наследнике виртуальный метод, нужно после его объявления написать ключевое слово override:
type
имя_класса_наследника=class (имя_класса_родителя)
...
...
end;
Рассмотрим наследование в классах на следующем примере. Создадим базовый класс Ttriangle (треугольник ) с полями классакоординаты вершин треугольника. В классе будут следующие методы:
- Proverka() — метод проверки существования треугольника (если 3 точки лежат на одной прямой, то треугольник не существует);
- Perimetr() — метод вычисления периметра треугольника;
- Square() — метод вычисления площади;
- Методы вычисления длин сторон a(), b(), c();
- Set_Tr() — метод получения координат;
- Show() — метод формирования сведений о треугольнике.
На основе этого класса создадим производный класс R_TTriangle (равносторонний треугольник), который наследует все поля и методы базового класса, но методы проверки и формирования сведений о фигуре перегружаются по другому алгоритму.
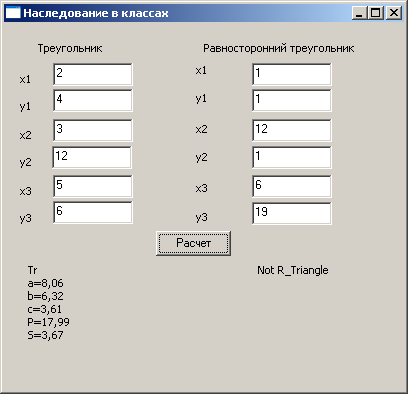
На форме поместим метку, кнопку и по 6 компонент типа TEdit для ввода координат вершин для двух треугольников. После щелчка по кнопке создаются два объекта типа "треугольник" и "равносторонний треугольник", вычисляются периметр и площадь каждого треугольника, и результаты выводятся ниже в компоненты Label15 и Label16. Далее приведён листинг программы с комментариями.
unit Unit1;
{$mode objfpc}{$H+}
interface
uses
Classes, SysUtils, LResources, Forms, Controls, Graphics,
Dialogs, StdCtrls;
type
{ TForm1 }
TForm1 = class (TForm)
Button1 : TButton; //кнопка "Расчёт"
//массивы x1, y1 - координаты вершин
//первого треугольника (частный случай)
//массивы x1, y1 - координаты вершин
//второго треугольника (равностороннего)
Edit1 : Tedit; //для ввода координаты x1[1]
Edit10 : TEdit; //для ввода координаты y2[2]
Edit11 : TEdit; //для ввода координаты x2[3]
Edit12 : TEdit; //для ввода координаты y2[3]
Edit2 : TEdit; //для ввода координаты y1[1]
Edit3 : TEdit; //для ввода координаты x2[2]
Edit4 : TEdit; //для ввода координаты y1[2]
Edit5 : TEdit; //для ввода координаты x1[3]
Edit6 : TEdit; //для ввода координаты y1[3]
Edit7 : TEdit; //для ввода координаты x2[1]
Edit8 : TEdit; //для ввода координаты y2[1]
Edit9 : TEdit; //для ввода координаты x2[2]
Label1 : TLabel;
Label10 : TLabel;
Label11 : TLabel;
Label12 : TLabel;
Label13 : TLabel;
Label14 : TLabel;
Label15 : TLabel;
Label16 : TLabel;
Label2 : TLabel;
Label3 : TLabel;
Label4 : TLabel;
Label5 : TLabel;
Label6 : TLabel;
Label7 : TLabel;
Label8 : TLabel;
Label9 : TLabel;
procedure Button1Click ( Sender : TObject );
private
{ private declarations }
public
{ public declarations }
end;
//объявление базового класса "треугольник"
type
TTriangle=class
Private
//массивы, в которых хранятся координаты вершин треугольника
x, y : array [ 0.. 2 ] of real;
Public
constructor Create; //конструктор
//метод получения исходных данных
procedure Set_Tr ( a, b : array of real );
//Методы вычисления сторон треугольника.
function a ( ) : real;
function b ( ) : real;
function c ( ) : real;
//Виртуальный метод проверки существования
//треугольника, который будет перегружен
//в производном классе.
function Proverka ( ) : boolean; virtual;
function Perimetr ( ) : real; //метод вычисления периметра
function Square ( ) : real; //метод вычисления площади
//виртуальный метод формирования сведений о треугольнике
function Show ( ) : string; virtual;
end;
//объявление производного класса "равносторонний треугольник"
type
R_TTriangle=class ( TTriangle )
public
//перегружаемые методы проверки, что треугольник является
//равносторонним,
//и формирования сведений о треугольнике
function Proverka ( ) : boolean; override;
function Show ( ) : string; override;
end;
var
Form1 : TForm1;
//объявление переменной типа класс "треугольник"
Figura1 : Ttriangle;
//объявление переменной типа класс "равносторонний треугольник"
Figura2 : R_TTriangle;
implementation
//Конструктор, который обнуляет
//массивы координат.
constructor TTriangle. Create;
var i : integer;
begin
for i :=0 to 2 do
begin
x [ i ] : = 0; y [ i ] : = 0;
end;
end;
//Метод получения координат вершин.
procedure TTriangle. Set_Tr ( a, b : array of real );
var i : integer;
begin
for i :=0 to 2 do
begin
x [ i ] : = a [ i ]; y [ i ] : = b [ i ];
end;
end;
//Методы вычисления сторон треугольника a, b, c
function TTriangle. a ( ) : real;
begin
a:= sqrt ( sqr ( x [1] - x [ 0 ] ) + sqr ( y [1] - y [ 0 ] ) );
end;
function TTriangle. b ( ) : real;
begin
b:= sqrt ( sqr ( x [2] _ x [ 1 ] ) + sqr ( y [2] _ y [ 1 ] ) );
end;
function TTriangle. c ( ) : real;
begin
c := sqrt ( sqr ( x [0] - x [ 2 ] ) + sqr ( y [0] - y [ 2 ] ) );
end;
//Метод вычисления периметра треугольника.
function TTriangle. Perimetr ( ) : real;
begin
Perimetr :=a()+b()+c( );
end;
//Функции вычисления площади треугольника.
function TTriangle. Square ( ) : real;
var p : real;
begin
p:= Perimetr ( ) / 2; //полупериметр
Squire := sqrt ( ( p -a ( ) ) * ( p - b ( ) ) * ( p - c ( ) ) );
end;
//Метод проверки существования треугольника:
//если в уравнение прямой, проходящей через
//две точки подставить координаты третьей точки
//и при этом получится равенство, значит три
//точки лежат на одной прямой и построение
//треугольника невозможно.
function TTriangle. Proverka ( ) : boolean;
begin
if ( x [0] - x [ 1 ] ) / ( x [0] - x [ 2 ] ) = ( y [0] - y [ 1 ] ) / ( y [0] - y [ 2 ] ) then
Proverka := false
else Proverka := true
end;
//метод формирования строки - сведений о треугольнике
function TTriangle. Show ( ) : string;
begin
//если треугольник существует,
//то формируем строку сведений о треугольнике
if Proverka ( ) then
Show:= ’ Tr ’+chr (13)+ ’ a= ’+FloatToStrF ( a ( ), ffFixed,5,2)+
chr (13)+ ’ b= ’+FloatToStrF ( b ( ), ffFixed,5,2)+ chr (13)+
’ c= ’+FloatToStrF ( c ( ), ffFixed,5,2)+ chr (13)+ ’P= ’+
FloatToStrF ( Perimetr ( ), ffFixed,5,2)+ chr (13)+ ’ S= ’+
FloatToStrF ( Square ( ), ffFixed, 5, 2 )
else
Show:= ’ Not Triangle ’;
end;
//Метод проверки существования
//равностороннего треугольника.
function R_TTriangle. Proverka ( ) : boolean;
begin
if ( a()=b ( ) ) and ( b()= c ( ) ) then
Proverka := true
else
Proverka := false
end;
//Метод формирования сведений
//о равностороннем треугольнике.
function R_TTriangle. Show ( ) : string;
begin
//если треугольник равносторонний,
//то формируем строку сведений
if Proverka ()= true then
Show:= ’ Tr ’+chr (13)+ ’ a= ’+FloatToStrF ( a ( ), ffFixed,5,2)+
chr (13)+ ’P= ’+FloatToStrF ( Perimetr ( ), ffFixed,5,2)+ chr ( 1 3 )
+ ’ S= ’+FloatToStrF ( Square ( ), ffFixed, 5, 2 )
else
Show:= ’ Not R_Triangle ’;
end;
{ TForm1 }
procedure TForm1. Button1Click ( Sender : Tobject );
//массивы x1, y1 - координаты треугольника
//массивы x2, y2 - координаты равностороннего треугольника
var x1, y1, x2, y2 : array [ 1.. 3 ] of real;
s : string;
begin
//чтение координат треугольников из полей ввода диалогового окна
x1 [ 1 ] : = StrToFloat ( Edit1. Text );
y1 [ 1 ] : = StrToFloat ( Edit2. Text );
x1 [ 2 ] : = StrToFloat ( Edit3. Text );
y1 [ 2 ] : = StrToFloat ( Edit4. Text );
x1 [ 3 ] : = StrToFloat ( Edit5. Text );
y1 [ 3 ] : = StrToFloat ( Edit6. Text );
x2 [ 1 ] : = StrToFloat ( Edit7. Text );
y2 [ 1 ] : = StrToFloat ( Edit8. Text );
x2 [ 2 ] : = StrToFloat ( Edit9. Text );
y2 [ 2 ] : = StrToFloat ( Edit10. Text );
x2 [ 3 ] : = StrToFloat ( Edit11. Text );
y2 [ 3 ] : = StrToFloat ( Edit12. Text );
//инициализация объекта класса "треугольник"
Figura1 := TTriangle. Create;
//инициализация объекта класса "равносторонний треугольник"
Figura2 :=R_TTriangle. Create;
Figura1. Set_Tr ( x1, y1 );
Figura2. Set_Tr ( x2, y2 );
//вызов методов формирования сведений и вывод строки на форму
s := Figura1. Show ( );
Label15. Caption := S;
s := Figura2. Show ( );
Label16. Caption := S;
//уничтожение объектов
Figura1. Free;
Figura2. Free;
end;
initialization
{$I unit1.lrs}
end.
Результаты работы программы представлены на рис. 9.3.
Абстрактный метод — это виртуальный или динамический метод, реализация которого не определена в том классе, где он объявлен. Предполагается, что этот метод будет перегружен в классе-наследнике. Вызывают метод только в тех классах, где он перезагружен. Абстрактный метод объявляется при помощи служебного слова abstract после слов virtual или dynamic, например:
Рассмотрим следующий пример. Создадим базовый класс TFigure (фигура). На основании этого класса можно построить производные классы для реальных фигур (окружность, четырёхугольник и т. д.). В нашем примере рассмотрим два класса-наследника TCircle (окружность) и TRectangle (прямоугольник). На форму поместим кнопку. При щелчке по кнопке инициализируются 2 объекта типа "окружность" и "прямоугольник", рассчитываются параметры фигур: периметр (длина окружности) и площадь. Результаты выводятся в компоненты Label1 и label2. Ниже приведён листинг программы.
unit Unit1;
{$mode objfpc}{$H+}
interface
uses
Classes, SysUtils, LResources, Forms, Controls, Graphics,
Dialogs, StdCtrls;
type
{ TForm1 }
TForm1 = class (TForm)
Button1 : TButton;
Label1 : TLabel;
Label2 : TLabel;
procedure Button1Click ( Sender : TObject );
private
{ private declarations }
public
{ public declarations }
end;
//объявление базового класса "фигура"
type
TFigure=class
private
n : integer; //количество сторон фигуры
p : array of real; //массив длин сторон фигуры
public
//абстрактный конструктор
//в каждом производном классе будет перегружаться
constructor Create; virtual; abstract;
function Perimetr ( ) : real; //метод вычисления периметра
//абстрактный метод вычисления площади, в каждом
//производном классе будет перегружаться реальным методом
function Square ( ) : real; virtual; abstract;
//абстрактный метод формирования сведений о фигуре
//в каждом производном классе будет перегружаться
function Show ( ) : string; virtual; abstract;
end;
//объявление производного класса "окружность"
type
TCircle=class ( TFigure )
public
constructor Create; override;
function Perimetr ( ) : real;
function Square ( ) : real; override;
function Show ( ) : string; override;
end;
//объявление производного класса "прямоугольник"
type
TRectangle=class ( TFigure )
public
constructor Create; override;
function Square ( ) : real; override;
function Show ( ) : string; override;
end;
var
Form1 : TForm1;
Figura1 : Tcircle; //объект типа класса "окружность"
Figura2 : TRectangle; //объект типа класса "прямоугольник"
implementation
//Описание метода вычисления
//периметра для базового класса.
function TFigure. Perimetr ( ) : real;
var i : integer;
s : real;
begin
s : = 0;
for i :=0 to n-1 do
s := s+p [ i ];
Perimetr := s;
end;
//описание конструктора в классе "окружность"
//перезагрузка абстрактного родительского конструктора
constructorTCircle. Create;
begin
//количество сторон для окружности 1
n : = 1;
//выделяем память под 1 элемент массива
SetLength ( p, n );
p [ 0 ] : = 5; //сторона - радиус окружности
end;
//Перезагрузка метода вычисления периметра.
function TCircle. Perimetr ( ) : real;
begin
Perimetr :=2 * Pi * p [ 0 ]; //вычисление длины окружности
end;
//Перезагрузка метода вычисления площади
function TCircle. Square ( ) : real;
begin
Square := Pi * sqr ( p [ 0 ] );
end;
//Описание метода формирования
//строки сведений об окружности.
//Перезагрузка родительского
//абстрактного метода.
function TCircle. Show ( ) : string;
begin
Show:= ’ Circle ’+chr (13)+ ’ r= ’+
FloatToStr ( p [ 0 ] ) + chr (13)+ ’P= ’+
FloatToStr ( Perimetr ())+
chr (13)+ ’ S= ’+FloatToStr ( Square ( ) );
end;
//Описание конструктора в классе прямоугольник.
//перезагрузка абстрактного
//родительского конструктора.
constructor TRectangle. Create;
begin
n : = 2; //количество сторон - две
SetLength ( p, n ); //выделение памяти под два элемента
p [ 0 ] : = 4; p [ 1 ] : = 2; //длины сторон
end;
//перезагрузка абстрактного родительского метода
//вычисления площади фигуры
function TRectangle. Square ( ) : real;
begin
Square :=p [ 0 ] * p [ 1 ];
end;
//Описание метода формирования
//сведений о прямоугольнике.
//перезагрузка родительского
//абстрактного метода.
function TRectangle. Show ( ) : string;
begin
Show:= ’ Rectangle ’+chr (13)+ ’ a= ’+
FloatToStr ( p [ 0 ] ) + ’ b= ’+
FloatToStr ( p [ 1 ] ) +
chr (13)+ ’P= ’+FloatToStr ( Perimetr ())+
chr (13)+ ’ S= ’+FloatToStr ( Square ( ) );
end;
{ TForm1 }
procedure TForm1. Button1Click ( Sender : TObject );
var s : string;
begin
//инициализация объекта типа "окружность"
Figura1 := TCircle. Create;
//инициализация объекта типа "прямоугольник"
Figura2 := TRectangle. Create;
//формирование сведений о фигурах и вывод результатов на форму
s := Figura1. Show ( );
label1. Caption := s;
s := Figura2. Show ( );
label2. Caption := s;
Figura1. Free;
Figura2. Free;
end;
initialization
{$I unit1.lrs}
end.